博文
Zmn-0859 薛问天: 给任意地图排四色标注的程序并不复杂
||
Zmn-0859 薛问天: 给任意地图排四色标注的程序并不复杂
【编者按。下面是薛问天先生的文章,是对许寿椿先生《Zmn-0835,0848》等文章的讨论。现在发布如下,供网友们共享。请大家关注并积极评论。另外本《专栏》重申,这里纯属学术讨论,所有发布的各种意见仅代表作者本人,不代表本《专栏》编辑部的意见。《专栏》中有些文章发扬了啄木鸟精神,对一些错误的观点和言论进行了说理的批评。但请大家注意,也有些有严重错误的文章在这里发布,就是为了引起和得到广大网友们的评论。不要以为在这里发布的文章都是正确无误的。】
给任意地图排四色标注的程序并不复杂
薛问天
 最近在科学网《数学啄木鸟专栏》中看到有关四色问题的讨论。确实在理论上严格证明,任何平面地图,都可只用4种颜色来标注各国(限制不允许在他国有超地),使邻国颜色不同。确实有一定的难度。甚至要借助计算机来证明。但是在实际上为任何地图安排四色标注这件事,在逻辑上并不复杂,只有一项明确的要求,那就是相邻国的颜色不同。因为邻国太多,因而人们用手脑直接去安排,是很费事的。但是用计算机编个程序去完成,则并不复杂。
最近在科学网《数学啄木鸟专栏》中看到有关四色问题的讨论。确实在理论上严格证明,任何平面地图,都可只用4种颜色来标注各国(限制不允许在他国有超地),使邻国颜色不同。确实有一定的难度。甚至要借助计算机来证明。但是在实际上为任何地图安排四色标注这件事,在逻辑上并不复杂,只有一项明确的要求,那就是相邻国的颜色不同。因为邻国太多,因而人们用手脑直接去安排,是很费事的。但是用计算机编个程序去完成,则并不复杂。
为此我就动手编了个程序,来为任何给出的地图,去找出四色标注的方案。这个程序很快就调试成功了。下面就简单介绍一下我用此程序为两个例图所求出的结果,我原以为可能程序要运行很长时间,但事实上很快。就在我普通的筆记本电脑上,不到一秒钟就可给出一个结果来,相当快。
例图1。
要让程序安排四色标注,当然首先要把地图的描述输入给程序。告诉程序地图中国家的数目等于多少,告诉图中哪些国家相邻。即如果用小于总国数的自然数0,1,2...,来表示各国家,就要表示有哪些i和j表示的囯家相邻。我们选的第一个例图就是所谓的Heawood反例,早先还有人认为它是不可以用四色标注的。

可以㸔出它用25个点来标明25个国家。用点同点之间有连线表明它们相邻。我们用0,1,2,...,24,来标明这25个点。于是用i#j来标明国家的相邻,例如在把这些数据输入给计算机后所显示的内容。

当计算机确认了这些输入的数据后,就可进行计算,并给出它的回答,为每个点给出标注的颜色,我们用0,1,2,3表示四种不同的颜色,于是计算程序就为每个点给出一个颜色来。这就是计算机对每个点i给出的gi的方案。

我们可以很快验明这个方案是正确的,即相邻的国家颜色不同。
这个程序不仅可给出一个方案,而是可以给出所有的合格方案。要知道满足邻国颜色不同的四色标注方案很多很多,我们不可能在这里一一列出,我们只在这里随意地现出第101个,第201个,第301个和第401个方案来,让大家看㸔。




程序最后给出,所有的合格的不同方案共513个。

当然这里只指的是不同构的方案,由0,1,2,3的任何不同排列构成的方案称为同构方案。如果把同构方案也㸔作是不同方案,那就更多,要乘上24 (=4!)。
例图2。
我们知道上图对地图的描述,是用点来表示国家,用点间的连线表示国家的相邻。而实际的地图是用线所围绕的空间表示国家,而由线相隔的国家是相邻的。我们为方便起見,仍以上图作为这样描述的地图实例,来进行一下实例计算。这样就需对每个空间标明国号,如下图。
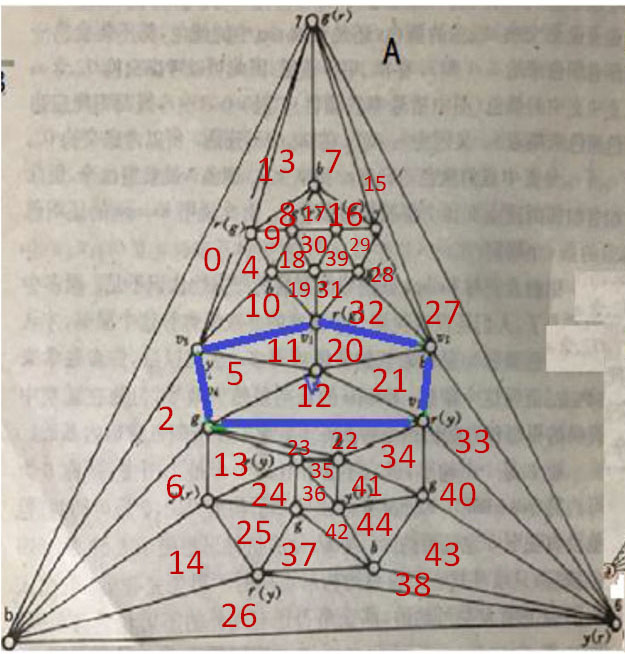
而国家间的相邻关系如下。这是计算机显示的国家间相邻的数据。
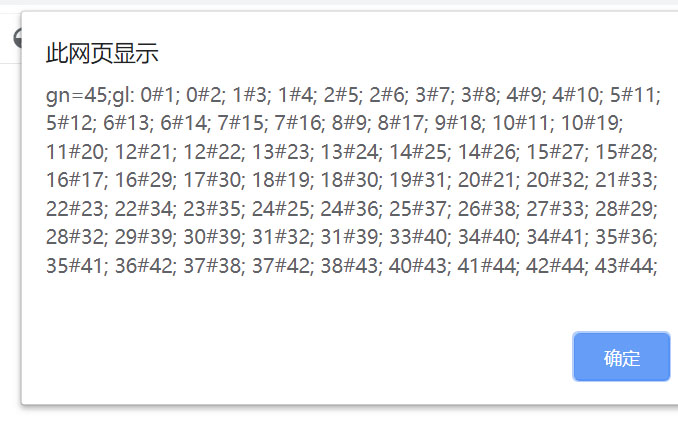
当程序确认了这些数据后,进行计算,很快就给出了四色标注的第1个方案来。

这个案例的合格方案比例1还更多,我下面显示它的第10方案,第100方案,第1000方案,第10000方案,第100000方案,第1000000方案,
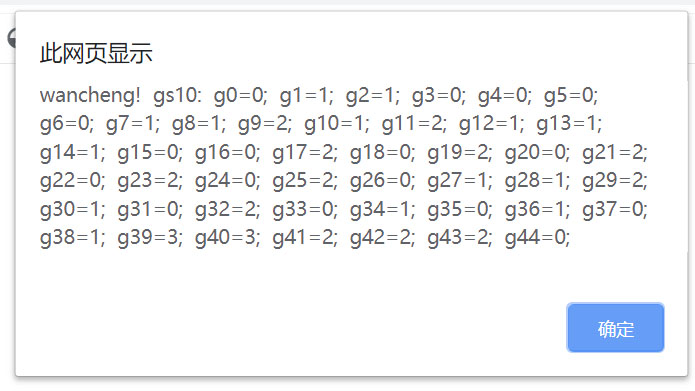


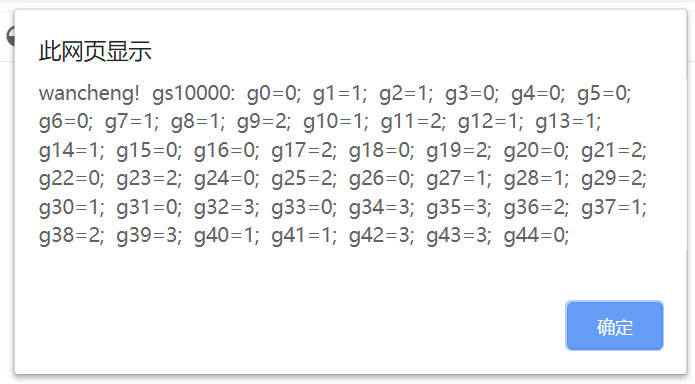
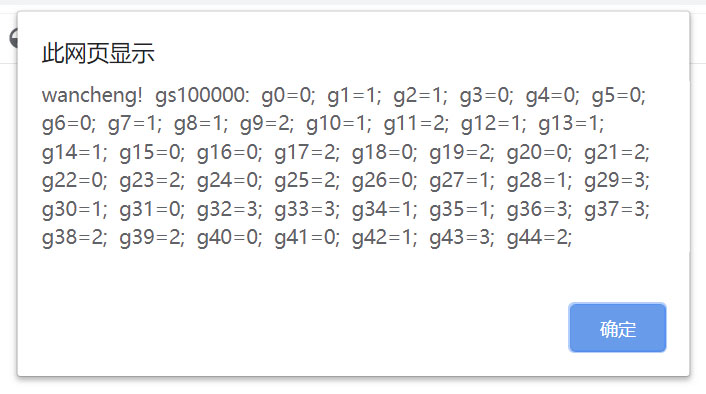
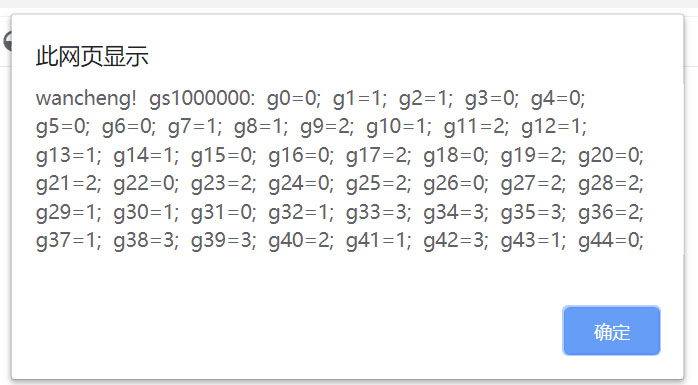
还没完,这些方案几分钟就做完了,不知还有多少方案,我没时间继续做下去了。如果需要,还可以继续做下去。直至全部完成。
最后我谈谈程序的结构。
这个程序并不复杂,相对是比较简单的。数据结构只有两个,一个表示地图的相邻,用一个二维向量(矩阵)gl( i,j)来表示,如果i国同j国相邻且i<J则令gl(i,j)=1,否则令gl(i,j)=0。再一个数据结构就是向量gs(i),表示所求方案中第i国的颜色。
程序中的函数只有一个,就是判断这样安排的国家颜色方案是否不合格,是否存在某个国的颜色同其相邻国的颜色相同。具体说就是判断是否存在i和j,使gl(i,j)=1而且gs(i)=gs(j)。
程序本身就是一个while循环语句,来为每个国家一个个地试探性安排颜色,然后判断是否合格,如果不合格则重新安排,如果全部国家的颜色安排后是合格的,则给出一个方案。然后再去给出第二方案,第三方案,...。等给不出合格方案时,就算出了全部合格方案的个数。
程序不长,也就是100行左右。程序并不复杂。但功能很全,能为任何地图安排出合格的四色标注方案,而且在需要时,所有合格的方案都可一一列出,并算出这些合格方案的个数。
返转到
zmn-000文清慧:发扬啄木鸟精神-《数学啄木鸟专栏》开场白及目录

https://blog.sciencenet.cn/blog-755313-1334288.html
上一篇:Zmn-0858 Thebeater: 回复薛问天先生0857
下一篇:Zmn-0860 许寿椿:回复Zmn-0859