博文
Zmn-0274 薛问天:教材没有错,是新华先生对微分的理解有错误。
||
Zmn-0274 薛问天:教材没有错,是新华先生对微分的理解有错误。
【编者按。下面是薛问天先生发来的文章。是对《Zmn-0243》新华先生的文章评论。现在发布如下,供网友们共享。请大家关注并积极评论。另外本《专栏》重申,这里纯属学术讨论,所有发布的各种意见仅代表作者本人,不代表本《专栏》编辑部的意见。】
教材没有错,是新华先生对微分的理解有错误。
薛问天
。
 新华先生在《.Zmn-0243 新 华: 三者都有错-评《条条评论条条错》》一文中谈到微分dy,dx概念 。他认为【教材确实有错 】,而且认为【不知是编写第二代微积分的作者没有弄清极限理论的本质,还是疏忽,......就把毫无关系的dy 、dx 与∆y 、∆x 扯到一起。】
新华先生在《.Zmn-0243 新 华: 三者都有错-评《条条评论条条错》》一文中谈到微分dy,dx概念 。他认为【教材确实有错 】,而且认为【不知是编写第二代微积分的作者没有弄清极限理论的本质,还是疏忽,......就把毫无关系的dy 、dx 与∆y 、∆x 扯到一起。】
其实微积分的教材没有错,而是新华先生对微分概念的理解有错误。
(一),微分dy,dx与函数的增量Δy,Δx【毫无关系】吗?
什么是微分。按照微分的定义,函数y=f(x)的因变量的微分dy是函数增量的线性主部,即Δy=dy+o(Δx),dy=f'(x)Δx是Δx的线性函数。函数y=f(x)的自变量的微分dx是函数自变量的增量Δx,即dx=Δx。 微分dy,dx与函数的增量Δy,Δx之间的关系如此密切,如此明确,不知新华先生从哪里得知 微分dy,dx与函数的增量Δy,Δx【毫无关系】,是【 没有弄清,,...还是疏忽】?
从直观的几何意义上讲 ,微分dy是切线函数的因变量增量, 微分dx是切线函数的自变量的增量。一个是曲线函数y=f(x)的增量,一个是相应切线函数y=y0+k(x-x0),k= f'(x0)的增量,怎么能没有关系呢?可见新华先生对微分是什么,并没有真正理解。下面我们来看看教科书中的一张解释微分概念的插图(菲书第174页):
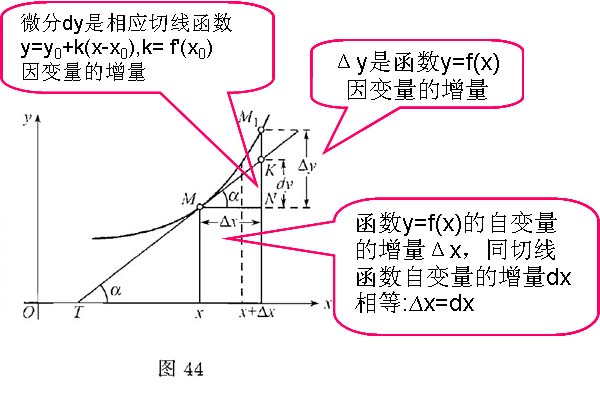
(二),∆x与dx是否真的【属性不同】,∆x【可以任意遨游】,而dx【只能一动不动】吗?
新华先生说【 ∆x与dx 属性不同,对一个确定的点,∆x 非常自由,在大于 0 的范围内可以任意遨游, dx则不同,只能一动不动】。
这是对微分变量这个概念的严重误解。微分的定义说得很清楚,函数的微分dy是Δx的线性函数,自变量的微分就是Δx,它们都是随着Δx的变化而变化的变量,怎么能是【一动不动】呢?
新华先生问道【 dy是定值,f'(x)是定值,而∆x是变量, dy=f'(x)∆ x两边属性不同,怎么能相等呢?】请问新华先生,你根据什么硬说 【dy是定值】呢?此式不是刚好说明dy是随着Δx变化的变量吗?
新华先生不知为什么要顽固地坚持这个 【dy是定值】的错误的观点。我在《 Zmn-0232 薛问天:谈数学中的「微分」和「极限」概念-评新华先生的错误观点。》一文中,专门有一小节「(一) (1),微分dy,dx是随着Δx变化而变化的变量,不是【不会改变】的【定值】。」就是特意评论新华先生的这个错误观点的。可是新华先生不听劝告也不说任何反驳的理由,在此文中仍然坚持此错误观点。
微商dy/dx是Δy/Δx在Δx→0时的极限。自然 Δy/Δx是变量。作为极限 dy/dx是定值,这肯定是对的,一点问题都没有。但由比值 dy/dx是定值就推断 dy和dx是定值就完全错误了。 dy和dx 并不是定值,它们是按比例,随Δx的变化而变化的变量。dy=f'(x)Δx,dx=Δx。可见 比值 dy/dx是定值它等于 f'(x),但 dy和dx 并不是定值,它们是按比例,随Δx变化的变量。
(三),定义需要怎样才算【公平】?
从新华先生的字里行间可以看出,他对微分的定义愤愤不平,很不满意 。关于自变量微分dx,他说【 把毫无关系的dy,dx 与∆y,∆x扯到一起,还强行定义 “∆x=dx”,】。关于因变量微分,他说【 不知编者出于何估计动机,要把dy与f'(x)∆x 配到一起,】。还说【 既然能通过特例∆y/∆x=dy/dx =1定义 “∆x=dx”,为什么不定义“dy=∆y”,这不明显的不公平吗?】
学习数学不必同「定义」较劲。数学定义本来就是一种规定,一种约定,它的本质无非是给数学对象起个名字。大家共同约定这个名字表示的数学对象表示的「是什么」。使大家讨论时有个共同的语言 。学习数学就是要通过定义来了解该数学对象的确切含义,属性。例如判定微分是定值还是变量,就是要依据微分的定义,这是一个共同的约定。而不是依据某个人的主观臆想。
要区别定义和定理的不同,定理是需要数学证明的,学习定理要问「为什么」。定义不需要证明,它就是一种规定和约定,不需要理由。学习定义要问的问题不是「为什幺」,而是要弄清「是什么」。这是学习数学的基本方法。
新华先生问,为什么要定义dx=Δx, 为什么不定义“dy=∆y”,问定义【出于何种动机】,是否【不公平】?这问的根本就是莫须有的问题,因为定义不需要理由。它就是一种规定。函数因变量的微分同自变量的微分是两种不同的微分,用不同的式子来定义,这很正常。不存在公平不公平的问题。怎样才算公平,不同的数学对象都用同一公式来定义 ,这才叫公平吗?
(四),关于自变量微分dx的两个等价定义。
从新华先生的提问 【 既然能通过特例∆y/∆x=dy/dx =1定义 “∆x=dx”,为什么不定义“dy=∆y”,】可以看出新华先生对函数自变量微分dx的两个等价定义,还没有完全理解。
关于函数自变量微分dx有两个等价定义,一个是直接定义,把函数自变量微分dx直接定义为等于自变量的增量Δx,dx=Δx。一个是把自变量x看作是恒等函数I(x)的因变量,从而把自变量的微分dx定义为恒等函数I(x)的因变量的微分:dx=I'(x)Δx。由于恒等函数的导数I'(x)=1,所以最后定义的结果仍然是dx=Δx。也就是说,证明了这两种定义是等价的。定义本身不需要理由,不需要证明。但是断定两种定义是「等价的」,则需要证明。
我想新华先生明白了对自变量微分的两种等价定义,就不会提出【 为什么不定义“dy=∆y”】这样的问题了,因为函数y=f(x)是以x为自变量的函数,它不是以y为自变量的函数,更不是以y为自变量的恒等函数。dy=f'(x)Δx同dy=Δy不等价。怎么能定义 “dy=∆y”呢?
(全文完)
返转到:
zmn-000文清慧:发扬啄木鸟精神-《数学啄木鸟专栏》开场白及目录

科学网《数学啄木鸟专栏》Zmn-000 到 Zmn-0250 期目录 2020-6-28 09:19
https://blog.sciencenet.cn/blog-755313-1244092.html
上一篇:Zmn-0273 李鸿仪:关于悖论的非客观性 。
下一篇:Zmn-0275 欧阳耿:《2500 多年来悬而未决的芝诺悖论家族成员------新发现的调和级数悖论》