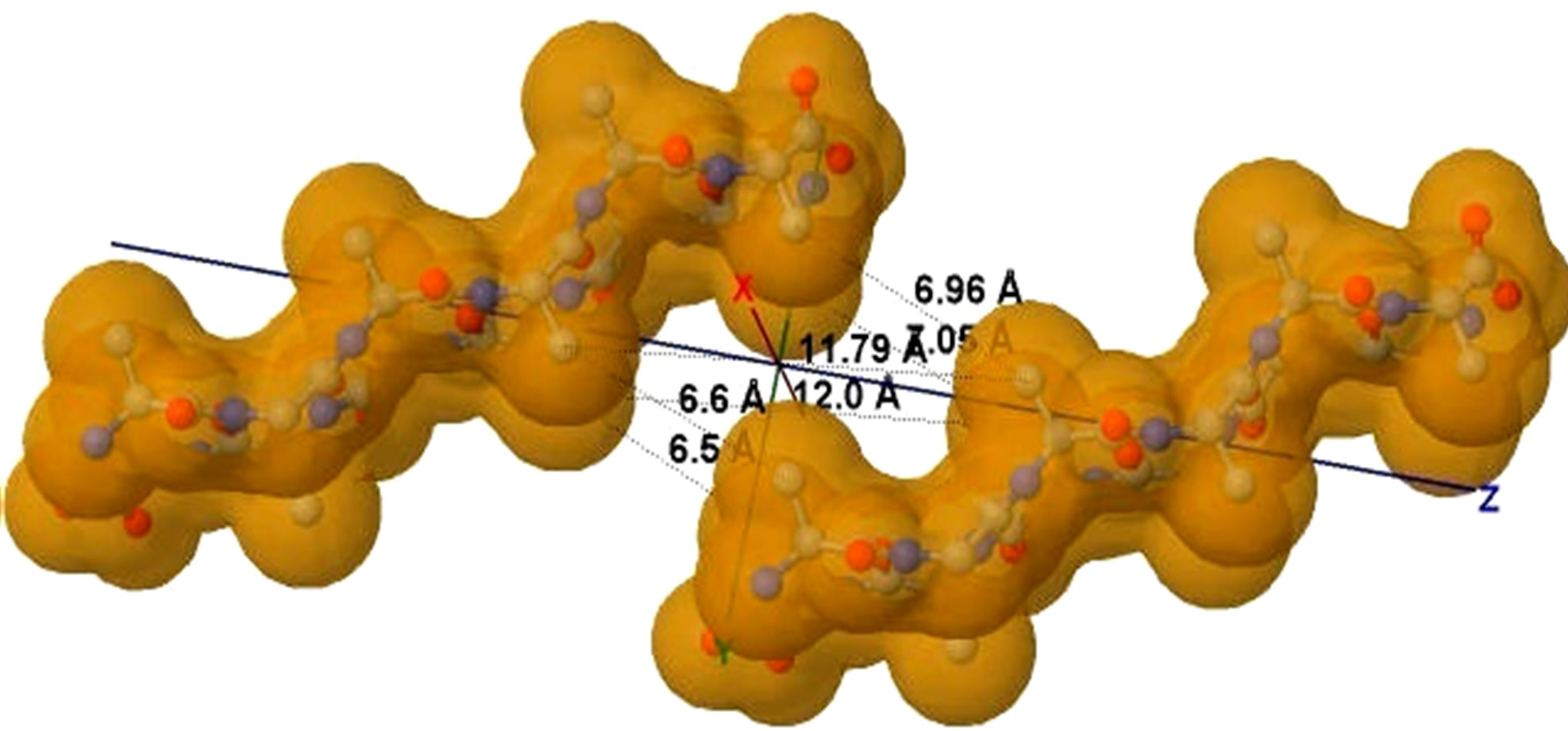
"蛋白質結構的數據表明大多數結構是由X射線衍射確定的，但是現在約10％的結構由蛋白質NMR確定。 當使用X射線衍射時，獲得蛋白質原子坐標的近似值，而通過NMR實驗發現蛋白質原子對之間距離的估計值。 因此，在後一種情況下，通過求解分子距离几何问题來獲得蛋白質的最終構象。一些蛋白质由低温电子显微镜确定。" (https://zh.wikipedia.org/zh-hans/蛋白質資料庫)

分子距离几何问题

 https://en.wikipedia.org/wiki/Distance_geometry_problem:

The distance geometry problem (DGP) is that of finding the coordinates of a set of points by using the distances between some pairs of such points.^[3] There exists nowadays a large community that is actively working on this problem, because there are several real-life applications that can lead to the formulation of a DGP. As an example, an interesting application is that of locating sensors in telecommunication networks.^[5] In such a case, the positions of some sensors are known (which are called anchors) and some of the distances between sensors (which can be anchors or not) are also known: the problem is to identify the positions in space for all sensors.

An interesting application arises in biology.^[4][6] Experimental techniques are able to estimate distances between pairs of atoms of a given molecule, and the problem becomes the one of identifying the three-dimensional conformation of the molecule, i.e. the positions of all its atoms. In this field, the main interest is on proteins, because discovering their three-dimensional conformation allows us to get clues about the function they are able to perform. The implications in related fields, such as biomedicine and drug design, are evident. When dealing with biological molecules, the DGP is generally referred to as molecular DGP (MDGP).

In the following, even if the article considers in general the DGP, the MDGP will be used as an example.

• Xplor-NIH. It has been particularly designed for solving instances of the problem in which the data come from NMR experiments, and it includes different functionalities. In particular, for the solution of the distance geometry problems, it makes use of heuristic methods (such as Simulated Annealing) and local search methods (such as Conjugate Gradient Minimization).

• TINKER. This is a package for molecular modeling and design. It includes many force fields for attempting the prediction of protein conformations from their chemical structure only. One of its functionalities, however, is to solve distance geometry problems.

Books and conferences[edit]

Crippen and Havel are two pioneers of DGP, and they co-authored the book "Distance Geometry and Molecular Conformation",^[4] 1988. Much more recently, an edited book, collecting the most recent efforts from the scientific community for solving the DGP, was published by Springer.^[3] See this web page for the list of contributions. https://link.springer.com/journal/10898/72/1/page/1  ...... Various conferences and workshops are held every year, where the focus is on DGP-related topics. However, the very first workshop completely devoted to DGP and its applications was held in 2013 in Manaus, Brazil: DGA13

1. Yemini, Y. (1978). "The positioning problem — a draft of an intermediate summary". Conference on Distributed Sensor Networks, Pittsburgh.

2. Liberti, Leo; Lavor, Carlile; MacUlan, Nelson; Mucherino, Antonio (2014). "Euclidean Distance Geometry and Applications". SIAM Review. 56: 3–69. arXiv:1205.0349. doi:10.1137/120875909.

3. Mucherino, A.; Lavor, C.; Liberti, L.; Maculan, N. (2013). Distance Geometry: Theory, Methods and Applications.

4. Crippen, G.M.; Havel, T.F. (1988). "Distance Geometry and Molecular Conformation". John Wiley & Sons.

5. Biswas, P.; Lian, T.; Wang, T.; Ye, Y. (2006). "Semidefinite programming based algorithms for sensor network localization". ACM Transactions in Sensor Networks. 2 (2): 188–220. doi:10.1145/1149283.1149286.

6. Blumenthal, L.M. (1970). Theory and applications of distance geometry (2nd ed.). Bronx, New York: Chelsea Publishing Company. p. 347. ISBN 978-0-8284-0242-2. LCCN 79113117.

7. More, J.J.; Wu, Z. (1999). "Distance Geometry Optimization for Protein Structures". Journal of Global Optimization. 15: 219–223. https://www.powershow.com/view1/73941-ZDc1Z/NMR_Structure_Refinement_powerpoint_ppt_presentation?varnishcache=1

8. Liberti, L.; Lavor, C.; Maculan, N. (2008). "A Branch-and-Prune Algorithm for the Molecular Distance Geometry Problem". International Transactions in Operational Research. 15: 1–17. doi:10.1111/j.1475-3995.2007.00622.x.

9. Mucherino, A.; Liberti, L.; Lavor, C.; Maculan, N. (2009). "Comparisons between an Exact and a MetaHeuristic Algorithm for the Molecular Distance Geometry Problem". ACM Conference Proceedings, Genetic and Evolutionary Computation Conference (GECCO09): 333–340.

10. Mucherino, A. (2013). On the Identification of Discretization Orders for Distance Geometry with Intervals. Lecture Notes in Computer Science. 8085. pp. 231–238. doi:10.1007/978-3-642-40020-9_24. ISBN 978-3-642-40019-3.

11. 距离几何优化问题：从美国计算机教授追回被抢车辆谈起: https://new.qq.com/omn/20190108/20190108A0DD4W.html

12. Springer ISBN 978-94-017-7317-1 Section 13.3 or Section 16.1

13. https://www.lix.polytechnique.fr/~liberti/dg17/:

"Consider the very easy problem: given a set of points in a Euclidean space, compute a subset of the pairwise distances. The fundamental problem in DG is the corresponding inverse problem: given a simple undirected graph with edges weighted by the distance values, as well as an integer K, compute a set of points in a K-dimensional Euclidean space which realize the given distances. The corresponding decision problem (i.e. determine whether or not there exists the realization) is called Distance Geometry Problem (DGP)."

"The function of proteins is determined by both chemical configuration and geometric conformation of the atoms. Some of the inter-atomic distances can be estimated quite precisely by chemical considerations (e.g. bond lengths and bond angles will yield all weighted triangles in the graph). Other distances can be estimated using Nuclear Magnetic Resonance (NMR). This yields a weighted graph, the realization of which in three-dimensional space provides a possible conformation of the protein."

"Studying nanostructures involves a variant of the DGP, called the unassigned DGP (uDGP). In this setting, retrieving the weighted graph from the NMR data is more difficult; the input to the uDGP is simply a sequence of distance values, without reference to their adjacencies. The uDGP asks to compute the realizations of the given sequence in 3D."

The impact of DG in applied mathematics

DG has been present in many sub-fields of mathematics.

• Heron’s theorem, which establishes a fprmula for computing the area of a triangle given the side lengths, is a milestone of elementary geometry.

• L. Euler stated a famous conjecture that topologically described closed polyhedra are rigid. Cauchy gave an elegant proof of the case where the polyhedra are geometrically described as the intersection of a finite number of half-spaces, and specifically strictly convex. This proof was extended to the case of non-strictly convex polyhedra by Alexandrov. In 1978, Robert Connelly finally disproved the conjecture by exhibiting a flexible non-convex topologically described polyhedron.

• One of J.C. Maxwell’s achievements was the graphical method for solving force diagrams. The method, based on a specific notion of duality for graphs drawn in the plane, achieves the balancing of degrees of freedom assigned to points and constraints imposed by segments in a way that is reminiscent to computations using the rigiditymatrix of a graph.

• A. Cayley formalized an algebraic equation that describes the geometrical notion of a tetrahedron with zero volume. Although Cayley worked in given dimensions, his ideas are eminently generalizable. This generalization was accomplished by Carl Menger, who also developed the first unified theoretical body of work wholly on DG. Many algorithms today are based on the Cayley-Menger determinant. The work of Menger was eventually carried on by L. Blumenthal.

• The only non-logical and non-philosophical work of K. Gödel is in the field of DG. Among other things, Carl Menger was the founder of the renowned Mathematische Kolloquium in Vienna. Stimulated by DG talks given by Menger and some of his students, collaborators and seminar lecturers, responding directly to a question posed at a certain seminar, Gödel proved that if four points are realizable in 3D, then they are also realizable on the surface of a sphere with the given distances being the length of geodesic tetrahedron sides. The proof rests on a fixed-point theorem that looks more innocent than it turns out to be.

• One of the most important algorithms in data science is Multi-Dimensional Scaling (MDS). Informally, it can be described as follows: given some estimation of discrepancies between objects, it represents the object in Euclidean spaces so people can have a visual representation that helps them make informal decisions. Formally, MDS takes an approximate finite metric on n elements, turns it into an approximate Gram matrix factors it, zeros the H negative eigenvalues, and takes the transpose of the factor to produce an n𝗑H matrix representation of a realization in H dimensions. This algorithm rests on a theoretical discovery in DG made in 1935 by Isaac Schoenberg (who also invented splines), namely the formula linking each squared Euclidean Distance Matrix (EDM) D and the corresponding Gram matrix, i.e. 2B=J D J, where n J = n I – 1^T1 and 1 is the all-one row vector.

• Another modern discovery used in data science and related to DG is the Johnson-Lindenstrauss Lemma (JLL). A wonderful piece of high-dimensional geometry which states something that is apparently very counter-intuitive, i.e.: for a finite set X of n points in an m-dimensional space and a given ε in (0,1) there exists a K = O(ε^-2 ln n) and a K𝗑m matrix T such that, for each pair of distinct x, y in X we have (1-ε)∥x - y∥₂ ≤ ∥T x - T y∥₂ ≤ (1+ε)∥x - y∥₂. Note that, surprisingly, the embedding dimension K is independent of the original dimension m, and only depends on the natural logarithm of the number of points in X. This discovery has been used in clustering, unconstrained optimization, statistics and is currently being applied to constrained optimization.