关于Sine-Gordon模型相变的一个简单图像

龚明，中国科学技术大学

Sine-Gordon（SG）模型是19世纪在数学上发现的一个重要的偏微分方程，它有孤立子解。孤立子有一定的能量，可以看作有质量的准粒子。同时，这个方程有相对论不变性。这个准粒子的质量和速度之间满足$m = m_0/\sqrt{1-v^2/c^2}$的关系，也就是相对论质量关系。在物理中，SG模型会存在相变，它会从无能隙（gapless）相变成有能隙（gapped）相。它是低维系统中最重要的一个场论模型，很多一维系统的有效理论最终都会变成SG模型； 比如XXZ模型、一维超导/超流模型等，它对应的是Luttinger液体。所以对它的理解就显得非常重要了---这是上个世纪70年代在量子场论方面的重要进展。但是一般教材都用到复杂的重整化群（RG）分析，又复杂又难懂。本文提供一个直观的图像 --- 我相信很多研究者也是这样理解的，尽管不一定在教材和文献中有直接讨论。从这个角度，这个模型的相变会变得非常简单。

我们从SG模型出发，它可以写成\begin{equation*} S = \int \mathcal{L} dxdt, \quad \mathcal{L} = {K \over 2} (\partial \phi)^2 + g \cos(\phi). \end{equation*}这里$K$为Luttinger参数，它是无量纲的，$g$为耦合常数。这个作用量可以用来计算配分函数，其中第一项对应高斯涨落。所以如果$K$很大，则高斯涨落会很小，这样涨落就局限在$\phi = 2\pi n$附近的很小的范围内。假设我们只关注在$\phi \sim 0$附近的振动，那么这个有效拉格朗日为\begin{equation*}\mathcal{L}={K \over 2} (\partial \phi)^2 -{g \over 2} \phi^2.\end{equation*}这就是著名的Klein-Gordon相对论方程，$g$的作用和质量$m$一样。可见耦合系数$g$引入一个能隙，这个模型是有能隙的，对应有能隙的相。这个时候，无论$g$多大，都会打开一个能隙，此时我们说$g$是相关的（relevant）。进一步，我们计算平均值就会发现，$\langle \cos(\phi)\rangle \ne 0$。

另一个极限，假设$K$很小，那么涨落在很大范围内都是允许的。这时，$\cos(\phi)$会遍历所有可能的值，我们可以期待\begin{equation*}\langle \cos(\phi)\rangle =0. \end{equation*}此时，无论$g$是多大，这个平均值都是等于零的。我们说，在这个相，$g$是无关的（irrelevant），它对应无能隙相。

因此，基于这个简单的图像，我们可以看出，SG模型在某个特殊点$K_c$存在相变，它会从一个有能隙（gapped）相变成无能隙（gapless）相。对于更复杂的模型，比如有很多个场的耦合的情况，也可以用类似的方式讨论。可以看出来，在绝大部分模型中，Luttinger参数$K$对相变起到了关键作用。我们甚至可以认为，$\langle \cos(\phi)\rangle$起到了序参量的作用。如果我们将这些结果拼凑在一起，可以得到下面的RG流方程\begin{equation*}{dg \over dl} = A (K-K_c) g, \end{equation*}其中$A > 0$。它说明，如果$K > K_c$, $g$会越来越大（relevant）；否则，它会越来越小（irrelevant）。因为本文的目的是介绍SG模型相变的整体图像，所以就不讨论参数$A$和$K_c$的具体值。但我们可估计$K_c$的值。利用相位的涨落的宽度为$\langle \phi^2\rangle = 1/K^2$,  设它和$\pi$差不多，则对应过渡到无能隙相，所以$1/K_c \sim \pi$，即$K_c \sim 1/\pi$。读者可以在很多教材中可以找到它们的具体值。

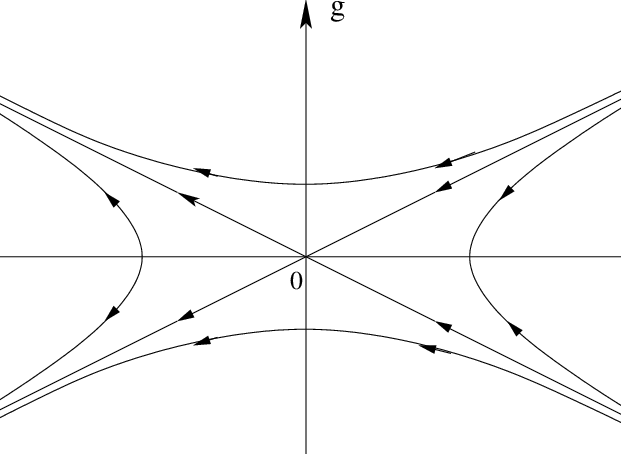
SG模型的RG流，图片来自网络

补充：关于SG模型的孤立子质量问题。考虑微分方程$\psi_{tt} - \psi_{xx} - g \sin(\psi) = 0$, 它的解为\begin{equation*}\psi = 4\arctan(\exp(a(x - vt))). \end{equation*}它是这个方程的解，可以确定$a = \sqrt{g/(1-v^2)}$。我们可以计算它的能量，扣除掉一个无关的背景，我们有\begin{equation*} E =\int  \psi_t^2/2 + \psi_x^2/2 + g \cos(\psi) dx = \text{background energy }+ {8\sqrt{g} v^2 \over \sqrt{1-v^2}} \sim mv^2.\end{equation*}具体计算见下面的代码。可见，这个结论和相对论方程几乎一样。这个问题曾经作为计算物理考试题，没有一个人做出来。后来有人告诉我，在孤立子教材中，这个结论广为人知。

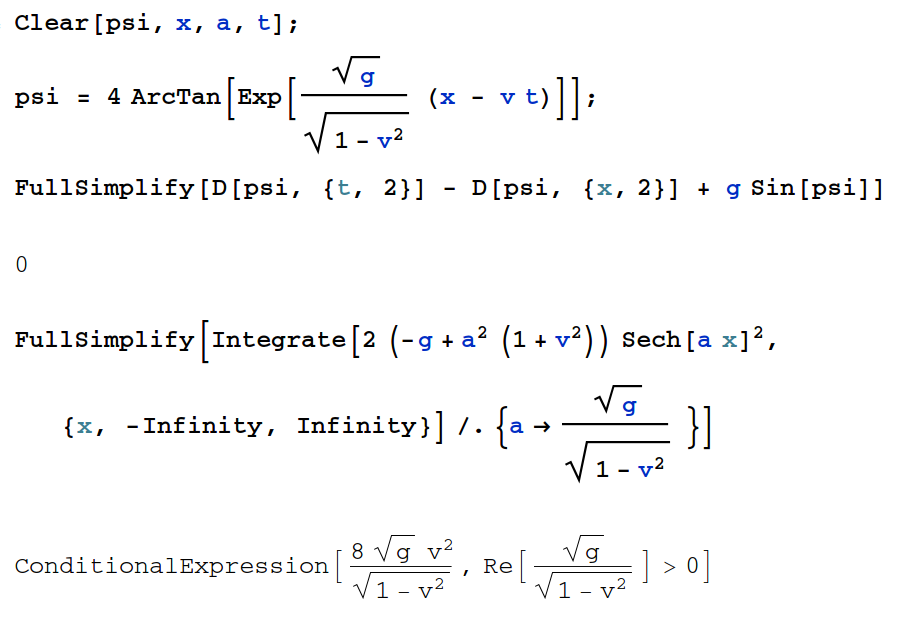
我的Mathematica计算代码

注：2022年春季，第二次讲这个模型的时候，我采用了这个图像。相比之下，2020年第一次就没有讲得那么清晰。