博文
关于一维玻色子有效模型的两个推导方法及其等价关系
|
关于一维玻色子有效模型的两个推导方法及其等价关系
龚明,中国科学技术大学
一维系统往往表现为Luttinger液体,而非普通的费米液体。一个典型的特点是,它没有费米面, 粒子的分布也不满足Fermi-Dirac分布。这是一种集体激发模式,类似声子,所以是一种玻色子。所以,无论是费米子、玻色子还是任意子,它们的激发都是这些玻色子,参数不同而已。所以其有效模型也一定是玻色子的有效模型。那么怎么推导它们呢?目前有两种方法较普遍,下面一一解释。
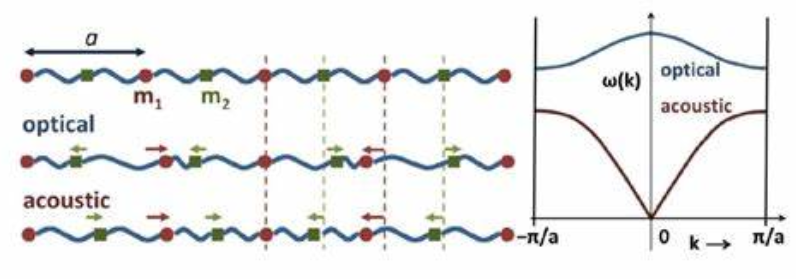
(声子模型,图片来自网络)
第一种方法可以参考文小刚的量子场论教材,它适用于任何维度。考虑下面的拉格朗日量\begin{equation}\mathcal{L} ={i\over 2} (\psi^* \partial_t \psi - \psi \partial_t \psi^*) - H, \quad H = {1\over 2} |\nabla \psi|^2 + {g \over 2} |\psi|^4 - \mu |\psi|^2. \end{equation}我们可以考虑相位-密度展开,即$\psi = \sqrt{n_0 + \delta n} e^{i\theta}$, $n=n_0 + \delta n$,那么可以得到\begin{equation*} \mathcal{L} = -n \partial_t \theta - {1\over 2} (|\nabla \sqrt{n}|^2 + n |\nabla \theta|^2) - {g\over 2} n^2 - \mu n.\end{equation*}假设$\delta n$是小量,同时考虑到作用量需要对$\int dx dt$做积分,所以$\int dx dt \delta n = 0$,这样忽略一个整体的常数$c$ --- 因为这个常数可以通过$\theta \rightarrow \theta - c t$消除掉。我们得到\begin{equation*}\mathcal{L} = -\delta n\partial_t \theta -{1\over 8m n_0} |\nabla \delta n|^2 - {g \over 2} |\delta n|^2 - {n \over 2m} |\nabla \theta|^2. \end{equation*}我们甚至可以直接扔掉第二项,因为密度的涨落是有能隙的,属于高频效应,是小量,所以\begin{equation*}\mathcal{L}= -\delta n\partial_t \theta - {g \over 2} |\delta n|^2 - {n \over 2m} |\nabla \theta|^2. \end{equation*}这个密度涨落的项和相位涨落的项是可以完全解耦合的,如果做一个平移,它们就无耦合了,这对应$\delta n$的鞍点(saddle point)。这样得到一个有效场论模型\begin{equation*}\mathcal{L} = {1\over 2g} (\partial_t\theta)^2 - {n \over 2m} |\nabla \theta|^2.\end{equation*}这个方程可以用来计算动量以及哈密顿。定义$\Pi = \partial \mathcal{L}/\partial \dot{\theta} = \partial_t \theta/g$,这样\begin{equation*}\mathcal{H} = \Pi \partial_t \theta - \mathcal{L} = {g \over 2} (\partial_t \theta)^2 + {n \over 2m} |\nabla \theta|^2.\end{equation*}从量子化条件,有类比关系$x\sim \theta$,$\Pi \sim p = \dot{x}$,所以$\Pi \sim \partial_t \theta$。我们也可以直接计算其运动方程\begin{equation*}{\partial_t^2 \theta \over g} - {n \over m} \nabla^2 \theta = 0, \quad \omega = v|k|, \quad v = \sqrt{{gn \over m}}. \end{equation*}这个结果是可以很容易解释:$n$越大,粒子数越多,则相互碰撞越频繁,声速越大;相反,质量越大,振动越难,碰撞越少,声速越小。我们可以想象一个无穷大质量的物体,连运动都困难,怎么可能传播声音呢?
因为这个方法适用于任意维度,上面的讨论其实也可以在Bose-Einstein凝聚的教材中找到。此外,如果利用Bogolibov变换,还可能更加严格地计算这个色散关系,当$k$大一点点,它会表现抛物势行为,此时$|\nabla \sqrt{n}|^2$项很重要,不可忽略。

(图片来自网络,它和玻色化有关)
第二种方法是利用Haldane的构造法,只适用于一维系统。Haldane是Luttinger液体这个名字的命名者。它提出\begin{equation*}\psi \sim \sqrt{n_0 - {\partial_t \theta}} e^{i\theta}. \end{equation*}知道动能的贡献主要来自相位场$\theta$,而相互作用的贡献主要来自粒子数涨落,所以有动能和势能\begin{equation*} T = {n \over 2m} |\nabla \theta|^2, \quad V = {g\over 2} (n_0 - {\partial_t \theta})^2.\end{equation*} 如果忽略那些不重要的常数,同时考虑到$\int dx \partial \theta =0$, 就可以得到\begin{equation*} \mathcal{H} = {g \over 2} |\partial_t \theta|^2 + {n \over 2m} |\nabla \theta|^2. \end{equation*}这个结果和第一个方法的分析得到的结果是一模一样的。如果我们回顾Haldane的原始论文,就会发现其实波函数的构造不是上面的那样,而是(因为是一维,我们令$\nabla = \partial_x = \partial$)\begin{equation*}\psi \sim (n -\partial \phi/\pi)^{1/2} \sum_m e^{i2m(\pi n x - \phi)}e^{i\theta}. \end{equation*}这个构造非常优雅漂亮,包含的意义也很深刻。保留$m=0$就足够了,其它项一般不重要。此外,利用量子化条件$[\theta, \partial \phi/\pi] = i \delta(x-x')$有$\partial \phi/\pi = \partial_t \theta$,这样就得到了上面的哈密顿。如果我们考虑一些周期外势的影响,此时周期外势可以弥补高阶项的动量传递,那么$m \ne 0$的那些项就有可能很重要了。
从上面的分析可以看出来,这两个处理是一致的。但是Haldane的方法更加普适,可以处理一些更复杂的问题。此外,如果抓住动能和势能的本质,那么和第一种方法相比,第二种方法毫无疑问更加简单和直观。但是它们各有优劣,比如第一种方法更加直观,而第二个方法则似乎是将第一个方法倒过来理解。但是,它们的使用范围很不相同:第一种方法适用于任意维度,而第二种方法则只适用于一维系统。据笔者了解,这两个方法在文献中都得到了广泛应用,都有自己的“爱好者”。
最后我们讨论一个问题,即如何把这个结果和Luttinger参数和速度联系在一起。假设\begin{equation*}\mathcal{H} = {v \over 2} ({(\partial_t \theta)^2 \over K} + K (\nabla \theta)^2). \end{equation*}得到$v=\sqrt{gn/m}$,$K = \sqrt{n/(gm)}$(见下图我的笔记的总结)。在Sine-Gordon模型中,如果考虑$g\cos(\theta)$,那么如果$K > K_c$,则存在相变,即系统会从无能隙相变成一个有能隙相。可见增加粒子数或者减小相互作用,都有可能实现这个相变。需要强调的是,这个相变和Mott相变不同,因为Mott相变要求在晶格中实现整数填充,而这里$n$可以是任意大于零的数。这个问题也比较容易理解,因为粒子数$n$足够多,才可能实现一个绝缘体。但上面的模型是没有办法实现这个绝缘体相,因为没有$\cos(\theta)$的项。这个可以很容易实现,比如加上一个很小的周期外势,就可以实现了【此时本质上就是Mott相变】。关于Sine-Gordon模型的相变,我在前面的博客中已经仔细讨论。

(来自我的笔记)
注:本文是对2020年,2022年我的讲课内容---玻色化---的整理和总结。
https://blog.sciencenet.cn/blog-709494-1382296.html
上一篇:关于Sine-Gordon模型相变的一个简单图像
下一篇:科学研究中习惯的重要性