数学已经成为人类步入现代化的核心工具与中心思想。大到卫星上天，小到一个app应用，都离不开数学──只是你是否知道而已。但是，请和我们哆嗒数学网的小编一起想象一下。远在数学还没有给我们带来计算机、量子力学和卫星定位系统之前的古代，一些最聪明的大脑已经在不断的发现他们的数学成就。这些发现建立了最基本的数学思想和工具，带领我们走进了现代化的生活。这是多么神奇的事情。下面列出的12位数学家，就是这些人中的佼佼者。他们的发现，形成了世界走入现代化的数学基石，也是我们步入现代生活最重要的一系列成就。估计外国人不知道秦九韶，高斯可能不算古代了。原文总结到1800年吧。

英国布莱奇利庄园6号楼的重建中发现了破解纳粹Enigma码的机密文件，文件是在2013年发现的，它被用于屋顶保温。文件包含了艾伦·图灵所设计的密码分析技术Banburismus已知唯一的样本。Banburismus被用于加快Enigma码的破解。英文：Molecular Warfare: Researchers Discover Viral 'Enigma Machine'。

计算机科学家吴恩达曾是Google的人工智能专家，如今则是百度的首席科学家，他接受采访谈论深度学习、神经网络、中英文翻译，以及对人工智能的看法。吴恩达指出，大脑中的神经元是不可思议复杂的机器，我们至今仍然无法理解，而模拟大脑的神经网络中的“神经元”则是极其简单的数学函数，只是模拟了生物神经元极小的一部分功能，人工神经网络只是受到了大脑的启发，与真正的大脑完全不可同日而语。 对于中英文理解，吴恩达称英文字母表只有26个字母，而中文有大约5000个常用汉字。除此之外，中英文的翻译还有一个问题是正确的对应，比如英文只有一个单词对应sister，而sister在中文里面有年长年幼之分（姐姐和妹妹）。吴恩达不认为人工智能会威胁人类，他相信人工智能将能改善无数人的生活，如果不是从根本上相信这一点他不会从事人工智能工作。他认为过于渲染了对杀人邪恶机器的恐惧，是“不必要的分心”，人工智能面临的最大挑战是劳工，它可能会导致许多人失去工作，比如无人驾驶汽车取代司机。吴恩达认为需要政界和商界领袖在这些问题上展开严肃讨论。

看这个图片漂亮吧？想知道怎么做出来的？想知道颜色怎么选择的？

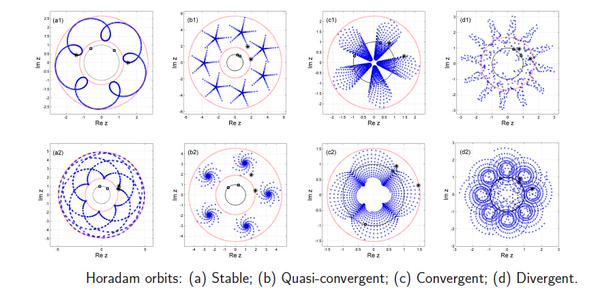
在自然界，艺术或科学中，众多几何图案可以从递归序列，诸如例如某些分形或费马螺线生成。斐波那契系列普遍存在于自然界中，击发了搜索技术，伪随机数生成器，或具有最佳性能的结构设计的灵感。

圆和方完全不同，它们之间有没有一个过渡？Gabriel Lame发明了一类曲线，把圆和方都包括进去。上色书就是一本完全用线条画出来的书，需要小孩子添上颜色。这需要充分的想象力。这里有一本Contours (PDF)，可以试试。

Zometool是一种用小棍子链接的玩具，可以组成各种奇妙的形状。

中国人的数学好，似乎是全世界公认的事实，但中国的数学研究却相当落后，为什么会这样？

迪林·王 (Dearing Wang) 的尺规作图，非常美丽。那这个图怎么画呢？John Edmark是另一位数学艺术家。他是斯坦福大学的兼职教授。上一期《数学都知道》介绍过了。

Beansprock是一家位于波斯顿的创业公司，它利用人工智能帮助软件工程师找工作。它会不会被领音 (LinkedIn) 干掉？

这是一组曲线的成像。作者：Hamid Naderi Yeganeh。

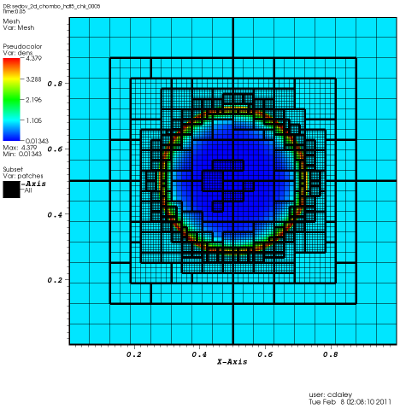
自适应网格（Adaptive Mesh Refinement，简称AMR）可以分为两类，其一是解域中格点总数保持不变，只是根据需要随时调整格点具体的位置；其二是实时将现有网格进一步细化，格点总数不再是常量。

当你在浴缸里舒舒服服地泡了个澡后，是否发现自己的手指却像葡萄乾一样起了褶子？一定是如此。这便是根据一种新的褶皱理论运算后得出的结果。手指、大脑、葡萄乾等很多事物的褶皱都可以用该综合理论来解释。该理论由一支麻省理工的工程师团队提出，并发表在 Nature Materials 期刊上。该综合理论能够帮助化学家更好地开发研究高科技材料。例如，在电子成像领域，化学家通过控制褶皱幅度对微型镜片的排列进行调整。褶皱现象也经常出现在生物领域。比如晶胚的发育便是通过球状细胞的聚合来完成的。这或许能帮助生物学家了解大脑等其他器官表面褶皱部分的重要性。

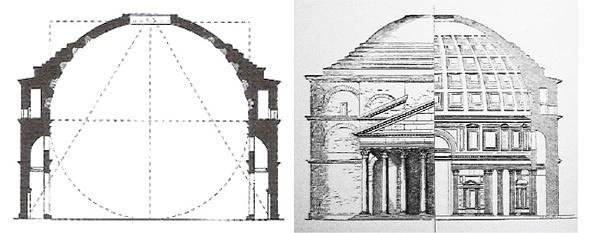
【神圣的罗马万神庙】歌德叹道：“渺小的、并习惯于渺小的人类，如何能将自己同这等高贵，宏伟的构筑物相提并论？”天光的引入一来给穹顶上的四边形凹格打下重重的阴影，加上这凹格自下而上不断缩小比例的变化，给人造成整个穹顶向上运动的透视错觉。（源自豆瓣，作者一行）

2015年2月3日美国国家数学研究所(MSRI)与美国普林斯顿高等研究院 (IAS) 联合宣布：首届美国国家数学节 (National Math Festival) 将在4月18日星期六于美国首都华盛顿召开。大名鼎鼎的史密森学会 (SI) 也将鼎力支持。

数学史上这个著名的大恩怨许多人在中学学习解方程时都听老师讲过。故事说，文艺复兴时期意大利数学家塔塔利亚发现了三次方程的解法，秘而不宣。一位叫卡当的骗子把解法骗到了手，公布出来，并宣称是他自己发现的。塔塔利亚一气之下向卡当挑战比赛解方程，并大获全胜，因为塔塔利亚教他时留了一招。不过，至今这些公式还被称作卡当公式，而塔塔利亚连名字都没有留下来，塔塔利亚只是一个外号，意大利语意思是“结巴”。网上广为流传的一篇《数学和数学家的故事》一文就是这么介绍的。然而，这个流行版本从总体到细节都是错误的。塔塔利亚不仅留下了名字（其真名叫尼科洛·方塔纳），而且也留下了有关这一争执的著作。后人对此事的看法在很大秤谌上就是受塔塔利亚一面之词的影响。

市面上有许多牛顿的传记，大多歌颂牛顿的科学成就或是提到那颗掉到地上的苹果，却遗漏或扭曲了牛顿的信仰。本文的目的在于：根据牛顿自己的手稿，说明信仰在牛顿科学生涯中所占的地位。

两个正五边形和一个正十边形在顶角可以紧贴在一起，它们的内角和正好是360度。但他们拼不出一个平面来。 相关阅读：五的烦恼

射影几何的诞生：为复兴射影几何作出杰出贡献的第一人是法国数学家彭色列。1812年他在参加拿破仑的俄罗斯之战时不幸被俘入狱。他在狱中凭记忆构思了巨著《论图形的射影性质》

看看集概率、统计、魔术师于一身的美国科学院院士、斯坦福大学教授如何谈数学。他曾经练过九年的钢琴。

英国利兹大学的数学教授Kevin Houston写了一本科普书，How to Think Like a Mathematician:（《如何像数学家一样思考》） 。为了给他的书作宣传，他特地制做了一个幻灯片：像数学家一样思考的10种方式（10 Ways To Think Like A Mathematician），很有趣。How to Think Like a Mathematician - Mathematical Thinking or Thinking Mathematically。

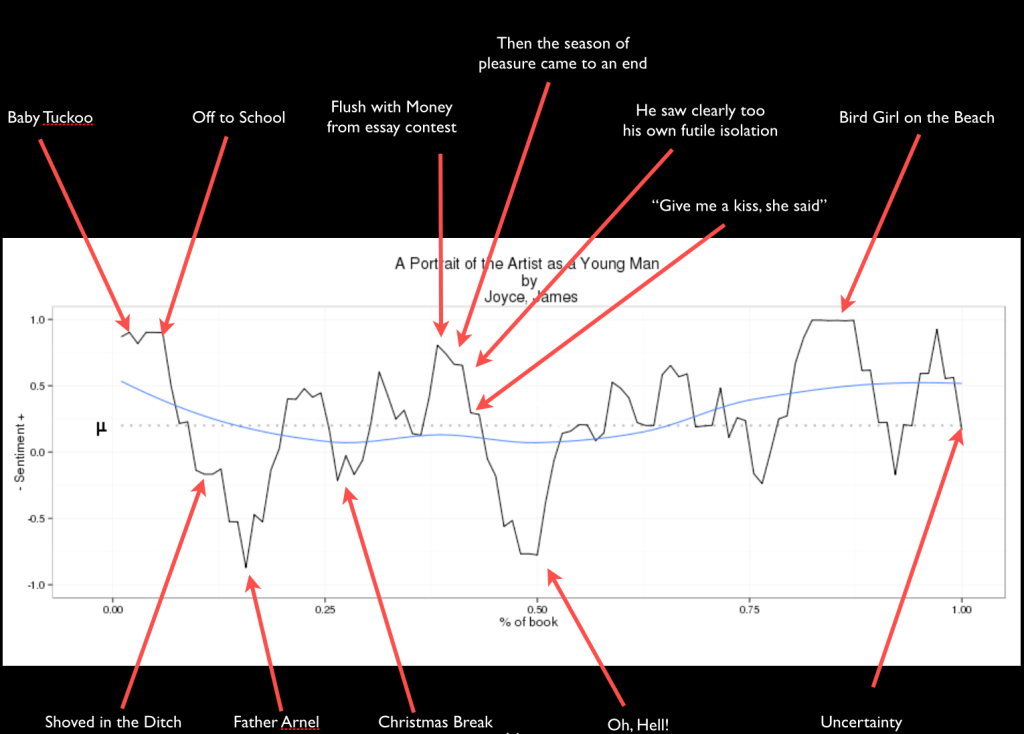
用情感分析做小说情节分析，挺有意思的想法，Vonnegut的shapes of stories小视频也很精彩，文中还引用了不错的情感分析主题的网页。

同一个笼子里养著鸡和兔子，它们共有88个头，244只脚，鸡和兔各有多少只？“鸡兔同笼”，鸡、兔共有107只，兔子的脚数比鸡的脚数多56只，问：鸡、兔各有多少只？鸡兔同笼，鸡比兔多12只，共有脚114只，求鸡、兔各有几只？

Linear Algebra (线性代数) 和 Statistics (统计学) 是最重要和不可缺少的。Calculus (微积分)，只是数学分析体系的基础。Partial Differential Equation （偏微分方程)，这主要用于描述动态过程，或者仿动态过程。Functional Analysis (泛函分析)，通俗地，可以理解为微积分从有限维空间到无限维空间的拓展──当然了，它实际上远不止于此。Measure Theory (测度理论)，这是和实分析关系非常密切的学科。但是测度理论并不限于此。Topology（拓扑学)，这是学术中很基础的学科。Differential Manifold (微分流形)，通俗地说它研究的是平滑的曲面。Lie Group Theory (李群论)，一般意义的群论在Learning中被运用的不是很多，群论在Learning中用得较多的是它的一个重要方向Lie group。Graph Theory（图论)，图，由于它在表述各种关系的强大能力以及优雅的理论，高效的算法，越来越受到Learning领域的欢迎。

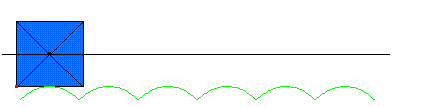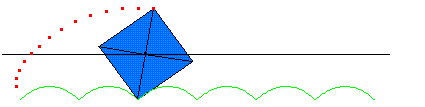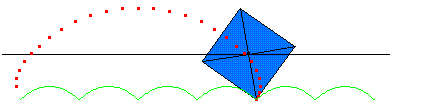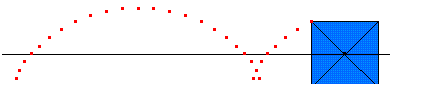
为什么所有汽车和自行车的轮子是圆的，现在我可以告诉你一个原因了，因为路是平的。   如果道路都按我方式来修建，那么轮子就必须得设计成方的，对，你没有听错轮子是方的，而且还是正方形的。

本文是作者刚刚度过数学专业的大一“菜鸟季”，写下的一篇数学分析学习心得，与各位网友分享。数学分析，简称数分，主要内容是微积分，是数学专业数学学习的开端，也是通往未来更高等数学的开端。同样，它是分析方向的基础，学好数学分析非常重要。

根据一个应用量子修正项补充爱因斯坦广义相对论的新模型，宇宙也许会永远存在。该模型还能解释暗物质和暗能量，一次解决了多种问题。论文（预印本）发表在《Physics Letters B》期刊上。该模型既没有预言创世大爆炸奇点，也没有预言宇宙大塌陷奇点。广义相对论预言的一个宇宙命运是它会开始收缩最终塌陷成一个无限密度点。新模型的提出者强调，他们的量子修正项并不是专门用来消除大爆炸奇点，认为量子校正可被视为宇宙学常数项（不再需要暗能量）和辐射项，使宇宙维持在一个有限尺寸，给予它无限的生命。                  

本文作者系我国已故著名数学家苏步青。年轻时，我在日本仙台的东北帝国大学留学。不久，认识了松本教授的爱女松本米子。在樱花盛开的季节，我们由恋爱而结婚。那年她二十三岁。她牺牲了自己的一切，帮助我在艰难的岁月里，取得了教学、科研上的一点成绩，她还担当起教育八个孩子的任务。我一直认为，没有我的夫人，我不可能培养出那么多的学生，取得数学研究上的成果。

最近出了孪生素数猜想、ABC猜想和最密堆积的进展，很多细节需要计算机的验证。是不是数学的本质发生了变化？这是一个特别值得注意的动向。

欣赏一下梳辫子中的数学，这世界真是什么人都有。Hacktastic是数学家laura Taalman的一个博客，是关于数学艺术设计和3D打印的。她有很多原始思想和她的程序，很宝贵。

不错的一个简介。

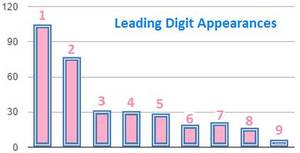
从1到9，如果上帝会选一个数字，应该是哪个？请相信，真有这么个最爱。本福德定律 (Benford's Law)

研究人员说，大脑通过把各种证据结合一起以达到一个决定，这和统计学家的思路是一样的。他们通过对猴子的观察发现它们需要多少信息来做出正确的决定。

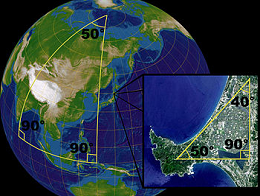
在数学家看来，平面和球面，是两种截然不同的几何，两种不同的世界观。让我们从最简单的面积测量开始说起。

曲面、三角分形、螺旋、多面体拼接、椭圆面…建筑师们都想成为现实数学家吗？

数学教授的主要期待：1. 学生可以通过补充证明细节 学到很多东西。2. 理解一个证明比提供每一步的证据更重要。3. 学生会在课外花时间去研究证明。4. 教授写出来的证明是重要的。那么学生呢？

很不错的一个介绍。

【绝美分形震撼于心】分形所呈现的无穷玄机和美感引发人们去探索。即使您不懂得其中深奥的数学哲理，也会为之感动。这是科学与艺术的融合，数学与艺术审美上的统一。

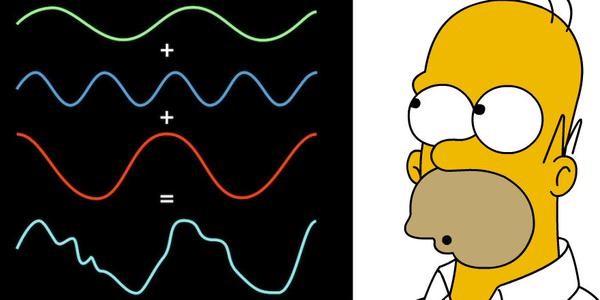
傅立叶变换是数学应用中最广泛的领域：光学，量子物理，射电天文学，MP3，JPEG压缩，X射线晶体学，语音识别，以及PET或MRI扫描。它甚至被James Watson和Francis Crick 用来解码DNA的双螺旋结构。Crick曾开玩笑说要写一本给看鸟人的傅立叶变换的书，因为James Watson喜欢看鸟。

国际数学家联盟第一位女掌门人的传奇：出生在比利时的煤矿区并在那里长大；学习的是理论物理，没有获得任何的数学学位，却成为了大数学家；写的小波十讲成为图像处理学子们的必读书 ... 推荐这位传奇女数学家的自述。

帕斯卡尔做出了帕斯卡尔三角形，即杨辉三角。傅立叶做出了傅立叶变换。把它们合二为一就成了上图。

数学越来越成为建筑学的一个不可分割的部分了。看看这些作品，没有数学行吗？

上一期介绍过。再来一遍。

文化是土壤，没有（数学文化的）肥沃土壤而期待长出（数学的）参天大树，结出（数学的）甜美果实，实无异于痴人说梦！

1939年，布尔巴基横空出世。虽然布尔巴基其人不存在，但以他名义出版的数学书却一本又一本，而且非常实在和严肃。虚构的布尔巴基是一位具有希腊名字，住在法国，且与虚构的南加哥大学相系－－只因主将韦伊曾在法国南锡和美国芝加哥工作过。

生活里，我们时常迷茫在两点之间的那条直线上，工作上，我们也时常死在两点之间的那条直线上，两点的魔咒，真的那么可怕吗？生活里，我们时常迷茫在两点之间的那条直线上，工作上，我们也时常死在两点之间的那条直线上，两点的魔咒，真的那么可怕吗？

痛苦是可微的，幸福是可积的，时间是可导的，在我的一生中，对大家的祝福，是单调递增的，是罗尔定理不可证明的，是拉格朗日中值定理无法推导的，综上所述，快乐是无界不可收敛的，是不能用换元积分法换元的。

96年胡平女儿出生的时候，张益唐负责开车接送。胡平：那以后，每逢我女儿过生日，张益唐就要寄一张200美元的支票来。我当然多次表示希望他不用寄了，因为我们知道他经济上也不宽裕，他坚持要寄，有几次我就没有去兑现。这张还是250，你看，01年的。他这种性格的淡泊、这种淡定，我想非常值得大家学习的。到04年，他领著他新婚的太太到我们家去，这样我们终于找到一个理由，我们说以后你就不要再寄了吧，有钱还是多给你太太寄去吧。张益唐：唐诗宋词？好吧，我就说两句吧，我不想说它的出处，好不好？“庾信平生最萧瑟，暮年诗赋动江关。”就这两句，可以吗？视频地址。

北京时间2月23日，第87届奥斯卡获奖名单全部出炉。 讲述数学家图灵故事的电影《模仿游戏》获得最佳改编剧本奖。 而剧中图灵的扮演者“卷福”在影帝的角逐中输给了《万物理论》霍金的扮演者“小雀斑”，被网友戏称“图灵”败给了“霍金”。视频

earchOnMath 旨在让学生和研究者找到包含给定一个数学公式的网页，给出不同的相似性。它是一个直接查询数学内容的搜索引擎。新春福利，初一送出！

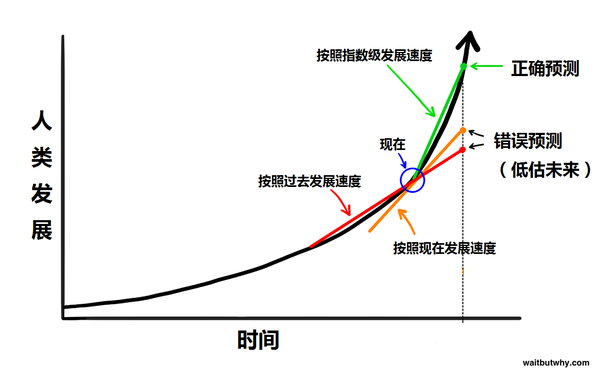
人工智能很可能导致人类的永生或者灭绝，而这一切很可能在我们的有生之年发生。这句话不是危言耸听，请耐心的看完本文再发表意见。

这是函数f(n) = n^2 + 2的图像。红点代表从0到999的数，灰色的箭头代表着如果把红点代表的数用于f(n)所得新点到原来点的连线。Python程序。

刚出了两期，葡萄牙人办的。

一个数学题的博客，特别是它的每日GIF。推荐。

本书对古今中外著名的数学故事用演义文体进行痛而不俗、深入浅出的论述。这本则属于中小学课堂学习新广角之一，也是一部世界数学简史，通过大家喜闻乐见的评书形式，风趣简明。不妨收藏一读。

PhotoMath是一款智能相机计算器。把照相机对准你的数学问题，PhotoMath就能给出答案来。要不要试一试？

机器学习的成功已经使得人们可以在不理解的情况下做出预测。而这个趋势是危险的。

圆周率日就要到了。你会怎样庆祝？人们都说，π是圆的，不是方的。这里有两个床被贴花，说明π也可能是方的。这是艺术家和数学家John Sims的作品。他专门为艺术家们写过一个可视数学课。这里是他的一个作品：树的平方根（Square Root of a Tree）。美国50个州的边界相形各异，有四四方方的，也有凹凸不规则的。知道哪个州是最规则的吗（矩形）？知道哪个州是最凹的吗？2013年10月2日一期《数学都知道》介绍过。

通常，数学一向被认为是透彻性、可靠性与有效性的化身。这使数学在人类学术中占有特殊地位。数学自明的概念、抽象的推理、确定的结论，赢得了哲学最持久的仰慕。哲学真理要立得住，就必须达到数学真理的层次。

在一个符合马尔可夫模型的稳态社会中，富人变穷人的可能与穷人变富人的可能的比例等于稳态社会中穷人与富人的比值。还是说人话吧，如果稳态社会中穷人是富人的四倍（二八原理），那么富人变成穷人的概率也要是穷人变富人概率的四倍。再换句话就是当贫富差距比例比较大的时候，若想维持社会中的贫富差距，富人变成穷人的风险要比穷人变富的概率大很多。那么稳态社会的富人就会说：我有我的资源与信息渠道，根据马太效应会越来越富，我不接受这个风险。那么好了，看上面的等式，稳态社会中穷富比不变，富变穷的风险不变，穷变富的可能也就被决定下来了，如果富变穷的可能非常小，那么穷变富的可能会比这个数还要小，要除以穷富比。换言之，稳态社会中富人如果想维持自己的个体富裕身份不变，只有通过挤压穷人变富的渠道才能完成。这样的社会只有通过集权或种性制度才能维持，在历史上似乎也长期被这种模式控制。

David Berlinski 在The Devil’s Delusion: Atheism and its Scientific Pretensions (Basic Books, 2009)一书里对达尔文主义“大不敬”，说进化论对科学的贡献（如果有的话）主要是意识形态的（it has much to offer their ideology）──这当然该遭严厉打击，我们的大学要坚决抵制西方意识形态的进化论的渗透。Gregory Chaitin 为了回应David，写书Proving Darwin：Making Biology Mathematical 。

原以为像张益唐这样潜心做研究，讲英语带口音，又不善交际的，讲课应该很一般。但看到ratemyprofessors.com（美国最流行的教师评价网）张益唐的网页，居然好评如流，平均分4.1，（最高是5）。有56个学生评价。除了一个之外，其它评价都是在张益唐出名之前写的。也有几个学生提到他的口音，但并不妨碍他们认为他是个好教师。另：张益唐现在不缺钱了

可以预见，相场模型中数学和力学问题的解决，归根结底还是要以材料为研究对象，促进材料学的发展，最终成为指导相关工艺设计的重要参考依据。从基础研究走向技术应用的路途虽然漫长，但只要不让两者从暂时的分工变成永久的脱离，坚守两者的不同人群不相互嘲讽，而是相互尊重各自的研究或应用，相互合作探讨，那么总是有希望的。

@ Gian-Carlo Rota在Discrete Thoughts (Boston: Birkh□user, 1997)中说，数学家有两种，一种是解题者（problem solver），一种是理论家（theorizer）。解题者内心保守，以为表述问题的概念是永恒不变的（The mathematical concepts required to state mathematical problems are tacitly assumed to be eternal and immutable）。理论家则是革命者，他们的成功不是解决老问题，而是让那些问题变得毫无意义。

不用相对运动概念建立平面运动刚体上两点的速度关系和加速度关系。

运用大数据分析方法，借助我们自己发明的“机器文学算法”，本文对诗仙李白、诗圣杜甫等的诗词进行了“用字习惯”分析。有些结果，与直观想像很接近；但是，确实另有一些结果比较出人意料，比如，1）如果不允□c李白使用姓氏字来写诗，那么，他连一个完整的诗句都写不成，更甭谈一首诗了；2）如果只允许李白使用姓氏字来写诗，那么，他连一首诗也写不出，但是，杜甫却能够写出三首诗来！

近年数学建模问题与结果：http://www.comap.com/undergraduate/contests/mcm/previous-contests.php，近年数学建模问题与结果的列表：http://www.comap.com/undergraduate/contests/matrix/index.html。另：龚林吉：2015年美国大学生数学建模试题，张慧铭：2015美国数学建模MCM A题翻译:Eradicating Ebola 根除埃博拉，张慧铭：2015美赛MCM B题翻译:Searching for a lost plane寻找失联的飞机，张慧铭：2015美赛MCM C题翻译:在组织中管理人力资本，张慧铭：2015美赛MCM D题翻译:这是可持续的吗？Is it sustainable?

为了能够准确地把现代通用计算机和其它各种计算机械区分开来，以计算机系统结构，亦即，现代通用计算机赖以工作的组织（逻辑）结构来定义计算机是必要的。从计算机系统结构的观点来看，能够被称之为现代通用计算机的计算机械必须同时满足下面三个必要条件：程序控制，程序内藏，程序可改。现代通用计算机自身的通用性，来源于程序控制；现代通用计算机的高速性，来源于程序内藏；现代通用计算机所能完成计算任务之多样性，来源于程序可改。巴贝奇的“解析机”的确是世界上第一台可编程通用计算机（为解析机编程的是英国诗人拜伦(G.G. Byron)的女儿、法国Lovelace伯爵夫人Ada，世界上第一位程序员；由美国国防部主导设计的通用程序设计语言Ada就是为了纪念她而命名），但它既不是程序内藏的，更不是程序可改的，故而不能被视为现代通用计算机。ENIAC的确是世界上第一台程序控制并且程序（褂讪）内藏（改良后的ENIAC）的计算机，但它不是程序可变的，故而不能被视为现代通用计算机。继续傧5c读：计算机与计算模式 (2) 何谓计算？。

数学家Jacob T. Schwartz（纽约大学Courant数学研究所数学与计算机教授）写过一篇很刺眼的文章：“The Pernicious Influence of Mathematics on Science”（文章重印见Discrete Thoughts: Essays on Mathematics, Science, and Philosophy, edited by Mark Kac, Gian-Carlo Rota and Jacob T. Schwartz, 1992），大概说数学只能玩儿简单游戏，复杂的就不行了。我过了一眼Jacob的文章，现在向大家传达精神：1）计算机死心眼儿，没想象力，头脑简单；2）即使最精确的科学也多少带著病态的近似；3）数学只能处理明确界定（well-defined）的情形，数学家把科学家的方便假定转化为公理，然后遵公理做事，把科学家也带坏了；4）因为数学无聊，没想象力，假如要适当用于科学，那么它需要证明的假定还得从更大的视野去寻找，而它自己是看不见的；5）数学没想象力，自然头脑简单，想证明一切──不管是辉煌还是荒谬，都给披上一套夺目的公式和定理的外衣；6）数学是骗人的戏法儿。如在统计力学中起著基本作用的Birkhoff各态历经定理，恰好证明了它只不过是各态历经假定上的一个无关紧要的超结构；7）数学论证巧妙隐藏了一些我们无知的东西，让我们看不到它省略的东西──这就是所谓数学的“一贯道”。如果Hardy见了Jacob对数学的批判，大概会说，看见了吧，数学本来是美好的，可惜被用坏了，用丑了。

作为科学皇后──魅力无穷的数学，竟然在一个小学生眼中成了死亡之源。而且是在武汉这样大城市里的小学生。她们的数学老师怎么啦？如何教的数学？在此情形下，多是孩子厌恶老师，转而厌恶所学内容。

陈景润张益唐可以说都算是幸运儿，他们的科研成果也可以说是：攻其一点，不及其余。多少年的艰辛努力，就攻一点，最后攻克了，他们的成果也很快得到了认可。比这两位无疑要卓越得多的伽罗华就没有那么幸运了。伽罗华开创了一个全新的数学分支，为人类数学史上的一代宗师，然他就是得不到与他同时代的那些当道的比他平庸得多的专家们的认可。为何如此？

如果用PPT的话，虽然也可一步一步显示，但总感觉节骤太快，画面停留时间短，学生跟不上或者跟得上但印像不深。

于丹心灵鸡汤的精髓可以用两个字来概括：“认命”，这是中国传统文化中“宿命论”的翻版（宿命论似乎起源于古巴比伦，现今的伊拉克），对解决问题毫无助益。数学作为思维科学，其作用无所不在，包括对人生的思考。数学工作者通常按照这样的方式思考：1、要解决什么问题或者想做什么事？2、这个问题的重要性体现在哪里或者为什么要做这件事？3、如何解决问题或者怎么做这件事？

罗伦兹认为，在大气运动过程中，即使各种误差和不确定性很小，也有可能在过程中将结果积累起来，经过逐级放大，形成巨大的大气运动。所以，长期的准确预测天气是不可能的。对初始值的极端不稳定性”，即：“混沌”，又称“蝴蝶效应”，亚马孙河流热带雨林中的蝴蝶拍拍翅膀，将使美洲几个月后出现比狂风还厉害的龙卷风！一只小小的蝴蝶，怎么可能造成巨大龙卷风呢，现实中这是根本不可能的发生的。那么，为什么“蝴蝶效应”计算机会推演出违背常识的结果呢？因为当前在电脑上演算的气象预测模型往往是有缺陷的、是有局限性的、是不完备的。

政府数据共享，目前证明，内部开放和共享是可能的，但对企业和公众开放还没有很好的案例。

个别人想抹黑数学的险恶用心是不会得逞的，正义的朋友们相信数学是美好和善良的。我怀疑S老师的数学已经被“缺心眼儿”计算机给洗脑了，已经失去了想象力，所以才会从那样可恶的角度去看数学，尽管有些话“事实上”是对的。

为什么一定要提出：定义多元向量除法?因为对应分量相除，“份量的商做商的份量”，是多元向量除法。

伯特兰罗素的墓志铭 (原文是拉丁文)：The third Earl Russell, O.M., Fellow of this College, was particularly famous as a writer on, and interpreter of, Mathematical Logic. Long appalled at human bitterness, as an old man - but with the verve of youth - he devoted himself entirely to the preservation of peace among nations, until finally, the recipient of numerous honours and a man respected throughout the world, he found rest from his labours in 1970, in his 98th year.

hand-waving argument是物理学家的习惯行为。在物理学的文献里，经常难以分辨究竟是作者认为如此还是作者证明如此。一个普通物理范畴里的问题，也会对hand waving专家构成严重挑战。

吴博士是上海交通大学的青年教师，在科学哲学、量子哲学、相对论方面具有广博知识和深刻的思考。我与他是在武汉赵国求教授组织召开的学术研讨会上认识的，并有一见如故的感觉。关于量子力学和相对论的科学基础问题，我们进行过多次交流，在观点上存在相似和不同之处。关于提出的氢原子电磁辐射耦合现象，他是理解的；但对于相对论，我们的观点和立场存在严重分歧。无论学术上的争论多么激烈，朋友之情一直是十分牢固的！！！最近，我们利用科学网博客再次对相对论的科学基础进行了争论，涉及到电磁学中的麦克斯韦方程组是否要求满足协变，这个最基本且重大的问题，同时也是我们如何理解和正确应用相对性原理的基本问题。我认为有必要写这篇博客再次重申一些基本的科学概念和定义。

网上流传著麻省老师的微积分课程视频，看了以后非常感慨。人家直接就讲导数，把极限当做工具来引出导数。不知道他们是否还另有一门极限课程。而且老师讲课非常注意突出导数和微积分的几何学意义、物理学意义、经济学意义，显得高等数学非常有用。我觉得这种课程设计和教学方式非常好，不仅易懂易学，而且可以激起学生的学习热情，明确目标和实用性。

研究形及其与数的相互关系和变化规律，发展为各种“几何学”。相对论认识到3维空间必须发展到时空弯曲的4维时空。为研讨相应的各种特性和运动规律，而创建了时空可变系多线矢，及其代数和解析矢算法则，用以表达并研讨客观存在的，现有理论尚未能解决的，各种已知有关实际问题，从而发展了相应的形与数的数学。相关连接：证明不可能有“无限长度的素数等差数列”。

本人不知道Laplace矩阵。于是搜索一番，遇到一个很不错的博客：http://blog.csdn.net/wangxiaojun911/article/details/7420965。原来Laplace矩阵不是别的，就是图(graph)的矩阵表示。

链路预测（Link Prediction）是网络科学中一个重要而有趣的基本问题，其最简单的数学形式是给定了已经观察到了网络结构，来预测可能被我们观察漏掉的，或者未来会出现的一些链路（Links）。精准的预测结果既可以指导生物学的实验──因为大部分我们观察到的生物网络，只是真实网络中很小的一部分，需要通过大量实验来确定其他的部分，还可以用来进行社交网络的好友预测──如果我们能够猜到你未来交友的趋势，这种“猜你要关注”的推荐就会变得非常精准。好的预测算法本身，还给出了很多网络演化可能机制的暗示。

作为网络的一个重要特徵度量，生成树与网络的众多结构及动态性质紧密相关，如稳定性、渗流、同步、随机游走等。本文通过递归枚举子图的方法求出了阿波罗（Apollonian）网络的生成树的精确数目和生成树熵。Apollonian网络隶属于极大平面图，并同时具备现实网络的显著特徵，如小世界，无标度，模块化，高集聚性等，因此，这项研究有重要的科学意义。研究表明，Apollonian网络的生成树性质与其它平均度相同的非无标度网络的生成树性质有明显的差异，说明了生成树与无标度等结构性质的关联性。另外，这一研究还有助于计算Apollonian网络的Laplacian矩阵的谱性质。

既然是研究slater行列式，就得追根溯源，细致考察其来龙去脉。结果发现，所谓slater determinant（行列式）其实最早是dirac给出的！早在1926年，紧随heisenburg和schrodinger之后，dirac就提出了这个行列式波函数作为全反对称系统的波函数。在这个文章里，dirac明确指出，如果电子的波函数服从全反对称条件的话，那么pauli不相容原理就成其一自然的推论。也就是在这个文章里，dirac提出了所谓的fermi-dirac分布。这个行列式最终被命名为slater行列式，大概与slater用这个行列式干了一件很漂亮的事情有关。

我已连续两年为陕西省国培学员授课：第一次是2013年12月22日，第二次为2014年12月25日。两次内容大致相同，皆是讲授数学之美，试图让更多学员真正认识数学、理解数学和享受数学。在网上偶然发现了两位学员的总结和感言，读后了解到小学数学一线教师的心声。

刷题对于数学研究作用不大，但是对考试作用很大，所以考试好的人不一定适合搞研究，适合搞研究的不一定考试好。而通过刷题才考试好的人一定不适合搞研究。

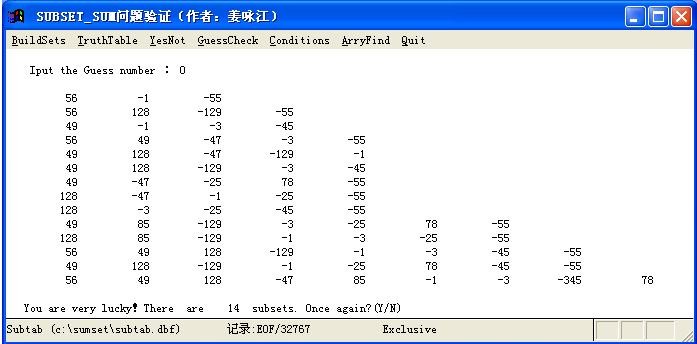
从图1可见15个元素的非空子集共有32767个，子集和为零的子集共有14个。恐怕第一个子集我们容易找到，越往下就越不容易了。这个问题涉及所谓的p与np的世界性难题。

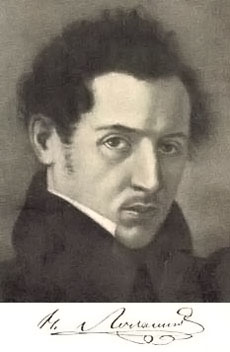
1829年2月23日一个寻常的下午，俄罗斯的喀山大学物理数学系学术会议上，罗巴切夫斯基（Nikolay Ivanovich Lobachevsky 1792-1856）有些激动而又忐忑地宣读著他的关于几何的论文──《几何学原理及平行线定理严格证明的摘要》，参加这次学术会议的学者不乏著名的数学家、天文学家、科学院院士等。然而，这位年轻的数学教授像是喝醉了，说的全是“胡话”。

当帕里比诺庄园主的小女儿在庄园里闲逛时，忽然发现墙纸上印著些奇怪的符号。好奇的大眼睛来回审视著这些符号，她开始了深思…原来庄园的女佣由于临时急用，把庄园主年轻时学习的高等数学讲义的纸页当作糊墙纸来用，应该是奥斯特罗格拉茨基所写的微积分讲义的一部分。这位名叫索菲娅的11岁小女孩居然对上面奇怪的数学符号和公式产生了浓厚的兴趣，她决定要弄懂这些符号…这个场景发生在十九世纪中叶的沙皇俄国。

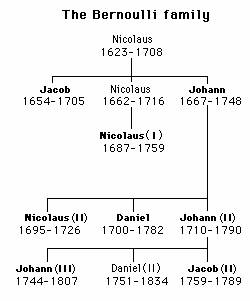
“倍儿努力”先生何许人？瑞士物理学家、数学家丹尼尔·伯努利(Daniel Bernoulli 1700～1782)是也。通用的译名念起来怎么听都有点像“不努力”，索性称呼为“倍儿努力”也许更贴切，注意要用京味儿的儿化音来读

目前坊间广泛流传的“负熵流”之说，肇始于薛定谔的“负熵”。而薛定谔的“负熵”则基于对“无序度”的研究。

众所周知，爱因斯坦几十年大统一梦的努力以失败而告终。以现在如笔者这样的马后炮观点看起来，爱因斯坦至少有两点缺失：一是低估了万有引力“桀骜不驯”的本性，二是选错了道，企图用经典场论，而不是量子场论来构建统一理论。也就是说，爱因斯坦忽略了更深入研究他自己参与创建的量子理论，也更忽略了量子理论后来几十年的发展。

感觉强烈的是生物数学的悄然兴起，俨然已成大势。研究工作紧贴实际，紧贴需求令人印象深刻。除了传统的流体力学问题，又有热门的金融数学问题，生物数学问题，还有新兴的纳米技术的数学模型，埃博拉病的传播和控制模型，气候变暖问题，交通问题等等。一个精华报告的题目是“Modelling atherosclerotic plaque formation:Boundaries, balances and bifurcation”，是关于粥样动脉硬化的课题。数学能如何帮助？

T：今天讲讲非欧几何。S：这是什么东东？

很早听老师上课传，大数学家德国人高斯(1777-1855)有个“圈子”论：人若画一个小圈子站内会觉得世界就这么大，画一个大圈站内会觉得世界很大。圈子论几乎切中绝大多数人的幸福感：圈子越小世界越小，幸福感越强，越觉得自己信息量很大，越自信、自我得很，这与“井蛙”特偶合。高斯的圈论特别适合吵吵闹闹的“知识分子”。

自72年起林家怯卩次回国讲学，每次都要解释懹τ檬??在自然科学中的作用，提醒中国国内对应用数学认识有误。2002年趁回国参加周老诞生百周年纪念大会之际明确提出中国需要发展“广义应用数学”，指出国内应用数学界所研究的只是“实用数学”。林专门用两个数学名词以示区别，为的是让国内学界澄清我们应该发展的是什么应用数学。

由于《论物质科学的关联》的成功，她成为风云人物。男性占绝对统治地位的剑桥大学的男教授们屈尊邀请她出席午餐会；她获得英国皇家天文学会等多家学术社团的名誉会员称号；虽然皇家学会一直没有接纳她，但为她塑了一尊大理石半身像，放在皇家学会大楼内。