作者介绍

刘威

东北大学秦皇岛分校控制工程学院

研究方向：智能交通；网联车辆协同控制。

魏仲洋

东北大学秦皇岛分校控制工程学院

研究方向：智能交通；网联车辆协同控制。

刘禹辰

东北大学秦皇岛分校控制工程学院

研究方向：非线性系统；车辆编队；智能交通。

高振宇

东北大学秦皇岛分校控制工程学院

研究方向：智能交通系统的控制、运行与优化；自主海洋航行器协同控制；信息物理系统。

学术成果：在 IEEE Transactions on Intelligent Transportation Systems、IEEE Transactions on Vehicular Technology、IEEE Transactions on Intelligent Vehicles、Ocean Engineering Information Sciences、International Journal of Robust and Nonlinear Control、Neurocomputing、《自动化学报》、《控制理论与应用》 等国内外控制领域权威期刊发表论文40余篇，SCI收录30篇。分别在Springer及机械工业出版社出版专著各1部。授权发明专利8项。

科研项目：主持国家自然科学基金项目1项、河北省自然科学基金项目2项 (面向项目1项、青年项目1项)、河北省教育厅高等学校研究项目1项、教育部中央高校基本科研业务费2项、东北大学科研启动费1项， 参与国家自然科学基金重点项目1项、 面上项目2项。 

学术兼职：担任自动化学会《综合智能交通专业委员会》委员、《车辆控制与智能化专业委员会》委员，担任 Journal of Automation and Intelligence、International Journal of Systems、Control & Communications 副主编。

文章亮点介绍

1. 文章设计了一种新的Nussbaum函数，用于应对执行器故障的未知时变方向。相比传统方法，新设计的Nussbaum函数振幅较小，不依赖于故障效率损失系数的精确边界值，大幅降低了控制设计中的复杂度。

2. 通过引入偏置约束函数，解决了非对称距离约束的问题，将其转化为对称问题。这种方法不仅简化了控制设计过程，还保证了系统的安全性和稳定性。

3. 为三阶车队系统提出了一种结合Nussbaum函数和对称障碍Lyapunov函数的方法，能够在设定时间内保证个体车辆稳定性和队列稳定性。

文章介绍

01、研究背景及目的

在智能交通系统 (ITS) 中，车队控制是一项重要的技术，能够显著提高交通流量、减少燃料消耗、提升驾驶安全。然而，车队中的车辆往往需要保持较小的间距以提高道路利用率，然而过小的间距增加了车辆碰撞的风险，特别是在车速较高时。为了确保行驶安全，距离约束问题成为研究的核心之一。

现有的车队控制方法主要依赖于两种常见的间距控制方法：规定性能控制 (PPC) 和障碍Lyapunov函数 (BLF) 方法。后者由于能同时满足稳定性和安全性要求，逐渐成为一种热门选择。然而，这些方法多局限于静态或已知的执行器故障模式，而现实中的执行器故障方向往往是时变且未知的。解决执行器故障问题对于车队控制的稳定性和安全性至关重要。

本文通过设计自适应固定时间容错控制器，解决车队控制中存在的时变执行器故障和距离约束问题。在此基础上，本文引入了Nussbaum函数处理未知的时变故障方向，并通过对称障碍Lyapunov函数简化控制设计过程，最终实现了车队的固定时间稳定性。

02、模型及结果分析

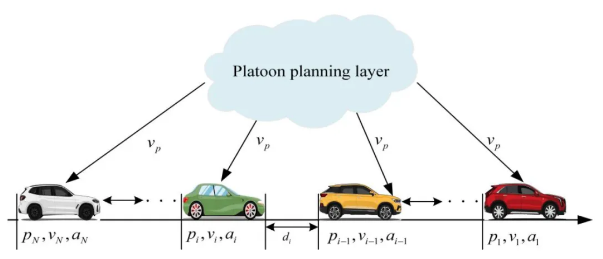
图1. 具有虚拟领导者的车辆排的交互结构

(1) 车辆动力学模型

本文首先建立了包含多个车辆的车队系统动力学模型，每辆车的模型为三阶非线性系统，状态变量包括位置、速度和加速度。该模型中引入了空气阻力、车道坡度等外部因素对车辆运动的影响：

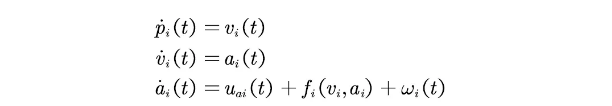
其中：

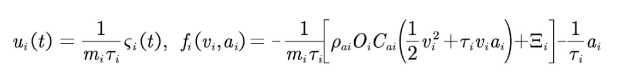
(2) 执行器故障模型

针对执行器故障问题，本文考虑了故障的时变方向和未知性。执行器故障表现为控制输入受到未知方向的干扰，具体通过效率因子和偏差故障来描述，这一模型更加贴近实际车辆的执行器工作情况：

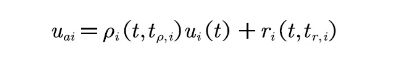
(3) 仿真结果

无故障情况下：仿真结果表明，在无执行器故障的理想情况下，本文提出的控制方法能够确保车队中的所有车辆在固定时间内达到稳定状态，车辆之间保持安全距离且不会出现碰撞；

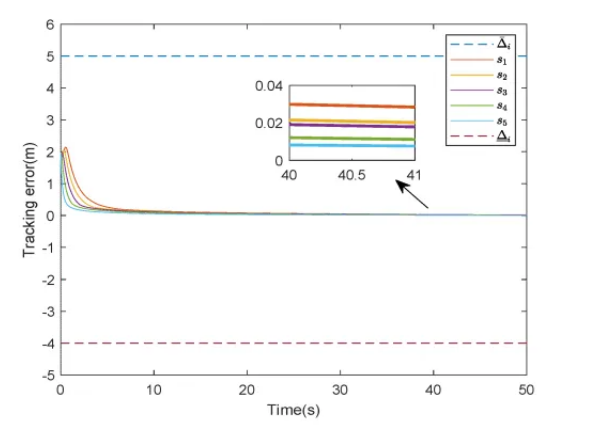
图2. 所提出算法在执行器无故障情况下控制的间距误差

故障情况下：即使在执行器故障方向未知且时变的情况下，控制器也能迅速调整控制输入，使得车队系统在短时间内恢复稳定，且确保队列的稳定性。

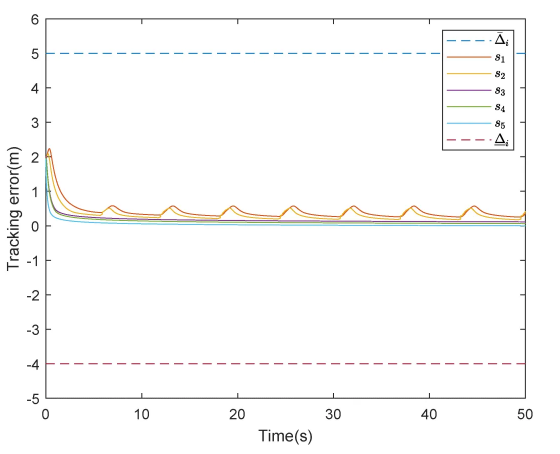
图3. 所提出算法在执行器故障情况下控制的间距误差

03、讨论与总结

本文提出了一种自适应固定时间容错控制方案，成功解决了车队控制中的时变执行器故障方向和距离约束问题。通过引入新型Nussbaum函数，控制器能够处理未知的故障方向，不依赖精确故障模型，同时结合对称障碍Lyapunov函数简化了非对称距离约束问题的处理，确保了控制器的设计简洁性和系统鲁棒性。仿真结果验证了该方法的有效性，无论在有无执行器故障的情况下，车队系统都能在固定时间内达到稳定状态，并确保个体车辆与队列整体的稳定性。在故障情况下，系统通过快速调整控制输入应对时变故障，表现出较好的鲁棒性和适应性。

原文出自 Mathematics 期刊：https://www.mdpi.com/2918740

期刊主页：https://www.mdpi.com/journal/mathematics

Mathematics 期刊介绍

主编：Francisco Chiclana, School of Computer Science and Informatics, De Montfort University, UK

期刊主题涵盖纯数学和应用数学所有领域，重点发表代数、几何和拓扑、函数插值、差分和微分方程、计算和应用数学、概率与统计、数学物理、动力系统、工程数学、数学和计算机科学、数学生物学、网络科学、金融数学、以及模糊集、系统和决策等相关领域的文章。现已被SCIE (Web of Science)、Scopus等重要数据库收录，JCR Category Rank: 21/489 (Q1)。

2023 Impact Factor：2.3

2023 CiteScore：4.0

Time to First Decision：17.1 Days

Acceptance to Publication：2.6 Days