博文
[小结] “P对NP, P vs NP, P versus NP”问题的博文汇集
||
真理越辩越明。
“什么伟大谦虚,在原则性问题上,从来没有客气过。”
物质世界是“普遍联系”和“永恒发展”的。
数学是现实世界中的“数量关系”和“空间形式”的科学。
汉语是联合国官方正式使用的 6 种同等有效语言之一。请不要歧视汉语!
Chinese is one of the six equally effective official languages of the United Nations.
Not to discriminate against Chinese, please!
[小结] “P对NP, P vs NP, P versus NP”问题的博文汇集
术语 terminology
P对NP: P vs NP, P versus NP problem
确定型图灵机: DTM, deterministic Turing machine
非确定型图灵机: NTM, non-deterministic Turing machine
集合论: set theory
策梅洛-弗兰克尔集合论: ZF, Zermelo–Fraenkel set theory
幂集: power set
幂集公理: axiom of power set
数学基础: foundations of mathematics
无穷: infinity
无穷公理: axiom of infinity
由 ZF 里的“幂集公理”可以发现:NTM 相当于 DTM 的幂集。
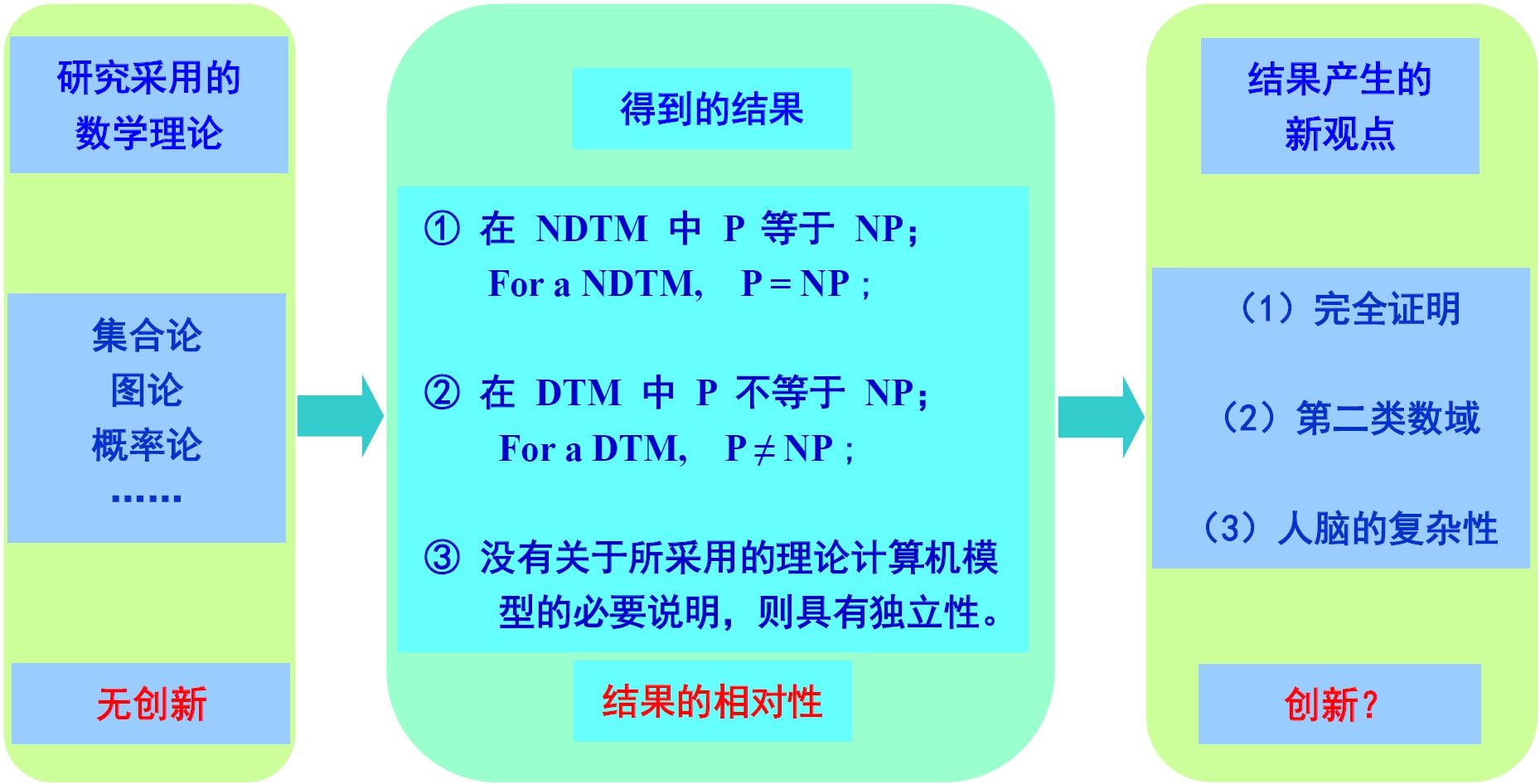
真正的“P对NP”问题和无穷没有任何关系。
The mainstream “P vs. NP” problem itself has nothing to do with infinity.

一、“P对NP”问题及其意义
请看:
[1] 2023-06-22,NP完全性/NP-completeness/许道云,中国大百科全书,第三版网络版[DB/OL]
https://www.zgbk.com/ecph/words?SiteID=1&ID=207239&Type=bkzyb&SubID=81689
[2] Stephen Cook. The importance of the P versus NP question [J]. Journal of the ACM, 2003, 50(1): 27-29.
doi: 10.1145/602382.602398
https://dl.acm.org/doi/abs/10.1145/602382.602398
[3] P vs NP, The Millennium Prize Problems, Clay Mathematics Institute
https://www.claymath.org/millennium/p-vs-np/
[4] 2022-01-20,时间复杂性类/time complexity class/许道云,中国大百科全书,第三版网络版[DB/OL]
https://www.zgbk.com/ecph/words?SiteID=1&ID=208077&Type=bkzyb&SubID=81685
[5] 2022-01-20,非确定多项式时间NP类/nondeterministic polynomial time class NP/许道云,中国大百科全书,第三版网络版[DB/OL]
https://www.zgbk.com/ecph/words?SiteID=1&ID=207012&Type=bkzyb&SubID=81685
一本汉译专著,比英文版内容更齐全:

(美)加里(Garey, M.R.),(美)约翰逊(Johnson, D.S.)著; 张立昂 沈泓 毕源章 译 吴云增 校. 计算机和难解性,NP完全性理论导引 [M]. 北京: 科学出版社, 1987-01。
二、发表的论文
[1] A non-canonical example to support that P is not equal to NP. Transactions of Tianjin University, 2011, 17(6): 446-449.
doi: 10.1007/s12209-011-1593-5
https://link.springer.com/article/10.1007/s12209-011-1593-5
[2] 第二类计算机构想. 中国电子科学研究院学报, 2011, 6(4): 368-374.
doi: 10.3969/j.issn.1673-5692.2011.04.009
https://d.wanfangdata.com.cn/periodical/dzkxjspl201104009
[3] 密码学与非确定型图灵机. 中国电子科学研究院学报, 2008, 3(6): 558-562.
http://qikan.cqvip.com/Qikan/Article/Detail?id=28856183&from=Qikan_Search_Index
[4] 人脑有多复杂?[J]. 百科知识, 1997, 7(总第216期): 39-40.
https://www.cnki.com.cn/Article/CJFDTotal-BKZS199707022.htm
[5] 人类智能模拟的“第2类数学(智能数学)”方法的哲学研究 [J]. 哲学研究, 1999, (4): 44-50.
https://www.cnki.com.cn/Article/CJFDTOTAL-ZXYJ199904005.htm
三、“P对NP”问题的博文汇集
[1] 2023-07-11,[请教,讨论] P对NP(十):一些相关的说明(研究思路、过渡参考资料等)
https://blog.sciencenet.cn/blog-107667-1394993.html
[2] 2023-07-10,[请教,讨论] P对NP(九):请您看看,您还有哪些批评或疑问?
https://blog.sciencenet.cn/blog-107667-1394865.html
[3] 2023-07-09,[请教,讨论] P对NP(八):“P对NP”为什么这么难?
https://blog.sciencenet.cn/blog-107667-1394724.html
[4] 2023-07-08,[请教,讨论] P对NP(七):“形转换”与立体图、平面图
https://blog.sciencenet.cn/blog-107667-1394594.html
[5] 2023-07-07,[请教,讨论] P对NP(六):无穷化版本与连续统假设CH
https://blog.sciencenet.cn/blog-107667-1394463.html
[6] 2023-07-05,[讨论] P对NP(五):宇宙“热寂”之前,“幂集公理”不会有太大的毛病?
https://blog.sciencenet.cn/blog-107667-1394169.html
[7] 2023-07-04,[请教] P对NP(四):相关要点小结(问答式)
https://blog.sciencenet.cn/blog-107667-1394027.html
[8] 2023-06-29,[请教] P对NP(三):“NP完全性, NP-completeness”之后
https://blog.sciencenet.cn/blog-107667-1393466.html
[9] 2023-06-28,[补充扼要说明] “P对NP, P vs NP”问题的“1+3”种证明与无穷
https://blog.sciencenet.cn/blog-107667-1393320.html
[10] 2023-06-27,[请注意] “P对NP, P vs NP”问题与“无穷 infinity”无关
https://blog.sciencenet.cn/blog-107667-1393194.html
[11] 2023-02-11,[随笔] “P对NP, P vs NP, P versus NP” Problem 问题:问题与求解方法
https://blog.sciencenet.cn/blog-107667-1375792.html
[12] 2023-01-18,[立此存照] 假如有人宣称证明了“P≠NP”,似乎只能证明他们不懂“什么是数学证明”
https://blog.sciencenet.cn/blog-107667-1372500.html
[13] 2023-01-17,[说明] 我对“P对NP”的所有研究,使用的都是现有的主流数学理论
https://blog.sciencenet.cn/blog-107667-1372343.html
[14] 2022-06-10,[请教] P对NP(二):结果的相对性与“1+3”种证明
https://blog.sciencenet.cn/blog-107667-1342404.html
[15] 2016-10-03,感谢“中国科学院科学智慧火花”:丘奇-图灵论题(Church-Turing Thesis),可能误导了 “P vs NP” 的研究
https://blog.sciencenet.cn/blog-107667-1006444.html
[16] 2016-09-27,平等的相对性与欺骗性(P vs NP):卡片机傻拍2016(132)
https://blog.sciencenet.cn/blog-107667-1005335.html
[17] 2015-12-24,感谢“中国科学院科学智慧火花”:某些 NPI 可能是处在相变边界的 NPC
https://blog.sciencenet.cn/blog-107667-945568.html
[18] 2015-05-22,The kernel of "P vs NP Problem": Axiom of power set!
https://blog.sciencenet.cn/blog-107667-892400.html
[19] 2012-03-23,[请教] P对NP:请***教授等专家指教(一) (一般背景知识汇报,无穷化版本下的“P对NP”)
https://blog.sciencenet.cn/blog-107667-550859.html
[20] 2011-12-05,TTU论文《A non-canonical example to support that P is not equal to NP》已经刊出
https://blog.sciencenet.cn/blog-107667-515297.html
[21] 2011-09-15,A FULL PROOF to the P versus NP problem “P对NP(P versus NP, P vs NP)”问题的一个“完全证明”
https://blog.sciencenet.cn/blog-107667-486692.html
[22] 2011-09-06,My report and papers on "the P versus NP problem" (P vs NP)
https://blog.sciencenet.cn/blog-107667-483639.html
[23] 2010-08-13,[请教]“P vs NP Problem”为什么这么困难?
https://blog.sciencenet.cn/blog-107667-352731.html
[24] 2019-08-10,[求证] 1967年朗兰兹 Robert Phelan Langlands 写给韦伊的信里说
https://blog.sciencenet.cn/blog-107667-1193149.html
[25] 2019-11-14,[求助] 什么是发表?什么是当前国际科技界承认的发表?
https://blog.sciencenet.cn/blog-107667-1206144.html
2023-07-19 后补,进一步请看:
[1] 2023-07-19,[新术语] 宇宙“均寂”(均匀地寂灭)与“幂集公理”
https://blog.sciencenet.cn/blog-107667-1395932.html
附录:一些近年的参考文献
[1] Lance Fortnow. Fifty years of P vs. NP and the possibility of the impossible [J]. Communications of the ACM, 2022, 65(1): 76–85.
doi: 10.1145/3460351
[2] Jorge A. Ruiz-Vanoye, Ocotlán Díaz-Parra, Francisco Rafael Trejo-Macotela, Julio Cesar Ramos-Fernández. Editorial: P versus NP problem from formal languages theory view [J]. International Journal of Combinatorial Optimization Problems and Informatics, 2021, 12(1): 1-8. Jan-April 2021
https://webdesignwaterloo.net/all-p-problems-are-np-problesm-scholarly-articles
[3] Luciana S. Buriol, Celina Figueiredo, Mauricio G. C. Resende, Eduardo Uchoa. The guide to NP-completeness is 40 years old: an homage to David s. Johnson [J]. Pesquisa Operacional, 2020, 40: e236329, 1-11
doi: 10.1590/0101-7438.2020.040.00236329
https://www.scielo.br/j/pope/a/Cw4K8K374SySpJdNdx9kPLx/?lang=en
[4] Juraj Hromkoviˇc, Peter Rossmanith. What one has to know when attacking P vs. NP [J]. Journal of Computer and System Sciences, 2020, 107: 142-155. February 2020
doi: 10.1016/j.jcss.2019.06.004
https://www.sciencedirect.com/science/article/pii/S0022000019300558
[5] Igor L. Markov. Limits on fundamental limits to computation [J]. Nature, 2014, 512((7513): 147-154.
doi: 10.1038/nature13570
https://www.nature.com/articles/nature13570
[6] Lance Fortnow. The Status of the P Versus NP Problem [J]. Communications of the ACM, 2009, 52(9): 78-86.
doi: 10.1145/1562164.1562186
https://m-cacm.acm.org/magazines/2009/9/38904-the-status-of-the-p-versus-np-problem/fulltext
参考资料:
[1] 2022-07-13,策梅洛-弗兰克尔集合论/Zermelo-Fraenkel set theory/杜国平,中国大百科全书,第三版网络版[DB/OL]
https://www.zgbk.com/ecph/words?SiteID=1&ID=229361&Type=bkzyb&SubID=104156
[2] 2023-01-18,数学基础/foundations of mathematics/何浩平,中国大百科全书,第三版网络版[DB/OL]
https://www.zgbk.com/ecph/words?SiteID=1&ID=456822&Type=bkzyb&SubID=137849
同时发展出的公理集合论成为了事实上的数学基础。
20世纪初数学基础研究的结果,是数学家们在实践中接受了公理化的集合论作为经典数学的基础。
E.F.F. 策梅洛、A.A.弗伦克尔(Adolf Abraham Fraenkel)等人发展出的ZFC(策梅洛-弗伦克尔-选择公理)公理集合论,是今天通行的公理集合论。ZFC公理集合论是万有理论,能够推导出经典数学的所有理论。
[3] ZFC. Encyclopedia of Mathematics. Zermelo–Fraenkel set theory with the axiom of choice
https://encyclopediaofmath.org/wiki/ZFC
[4] Turing machine. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Turing_machine
[5] Nondeterministic Turing machine. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Nondeterministic_Turing_machine
[6] Power set. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Power_set
[7] Church thesis. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Church_thesis
[8] Infinity, axiom of. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Infinity,_axiom_of
感谢您的指教!
感谢您指正以上任何错误!
感谢您提供更多的相关资料!
https://blog.sciencenet.cn/blog-107667-1395804.html
上一篇:[小资料] 梵高的“卧室”一个画了三幅(Van Gogh’s Bedrooms)
下一篇:[新术语] 宇宙“均寂”(均匀地寂灭)与“幂集公理”