地球内部的压强有多大？

中国科学技术大学，龚明

游泳的时候，我们可以感受到来自水的压力；潜水越深，压力也就越大。类似的，如果我们对一块砖头施加足够大的压力，它会被粉碎。这也是为什么山峰不能超过几十千米的原因。那么，我们自然会问，在地心处，其压强有多大？ 这个问题可能让无数孩子和科学家着迷 --- 我们回想一下一百多年前凡尔纳的小说《地心游记》，以及近二十年拍摄的相关电影就清楚了。目前人类能探测地球的最深处也就10千米左右，和地球的6400千米的半径相比，这只是地壳表面薄薄的一层。我们对地幔、地核的性质了解就更少了。我们进一步可能会继续问，地球内部是固体，还是液体，以及其温度有多高等等。这些问题都很重要，但这篇文章我们中关注一个问题，即地球内部的压强到底有多大？我们只需要用最简单的力学知识，就可以了解这一点。

首先，让我们假设地球内部和水一样，其压强随着深度满足阿基米德公式 \begin{equation*} P(0) = \rho g R. \end{equation*} 其中密度$\rho = 5.5 \times 10^3$ kg/m$^3$，加速度$g = 9.8$ N/kg，半径 $R=6371$ km。我们还可以利用$g = G M/R^2$，其中地球质量$M = 4\pi R^3 \rho/3$，那么得到\begin{equation*}P(0) = {4\pi G \rho^2 R^2\over 3}. \end{equation*}这里万有引力常数$G =6.67 \times 10^{-11}$ $m^{3}$ kg$^{-1}$ s$^{-2}$。代入参数直接计算可以得到地心处的压强\begin{equation*} P(0) = 343 \text{ GPa}. \end{equation*}这是一个巨大的压强，但目前可以在实验室实现； 比如最大的金刚石对顶砧实验可以实现超过500 GPa的压强。不过这个估计，忽略了一个细节，即重力和深度有密切关系。所以上面的估计其实是不太准确的。为此，我们不妨假设地球密度是均匀的，但是压强和深度有关，所以我们有\begin{equation*} dF =  (P(r) - P(r+dr)) dS = G (4\pi r^3\rho/3) \rho dS dr /r^2. \end{equation*} 这个方程其实利用了在$r$处压力和重力处处平衡，得到 \begin{equation*} P(0) = {2\pi G \rho^2 R^2\over 3}. \end{equation*} 这个结果是上面的粗糙估计的一半，所以我们有\begin{equation*} P(0) = 171.5 \text{ GPa}. \end{equation*}

第二个估算也不太准确，它忽略了很多重要的因素，比如在地下，随着温度升高，压强也增大。这个结论可以从热力学最基本的公式$PV = NRT$可以得到 --- 假设对固体它也定性成立。同时，我们也忽略了密度的影响。随着压力增大，原子之间间距减小，密度会增大。考虑这些因素，压强可能在二者之间，也可能比二者都大。的确，我们查资料就可以看到，这个压强在 360 - 370 GPa，和我们的估计相差不大。这么大的压强，所有固体的晶体结构都被破坏掉了，原子呈现出完全不同的样子。此外，地心处温度很高，原子最可能形成液体的状态，但这种液体的物理性质，一定和地球表面的液体性质完全不同。既然是液体，显然越重的元素越应该处于地球的核心。很多科学家提出，地心应该是液态铁构成的，这种元素的运动，可能是地磁场起源的重要原因。这个神秘的状态，目前是高压物理的研究重点，在将来科学家可能可以在实验上实现它们。可见，尽管今天的科学已经取得了很大的进步，我们对脚下的土地，依旧有太多不了解的地方。

（地球内部结构，图片来自网络）

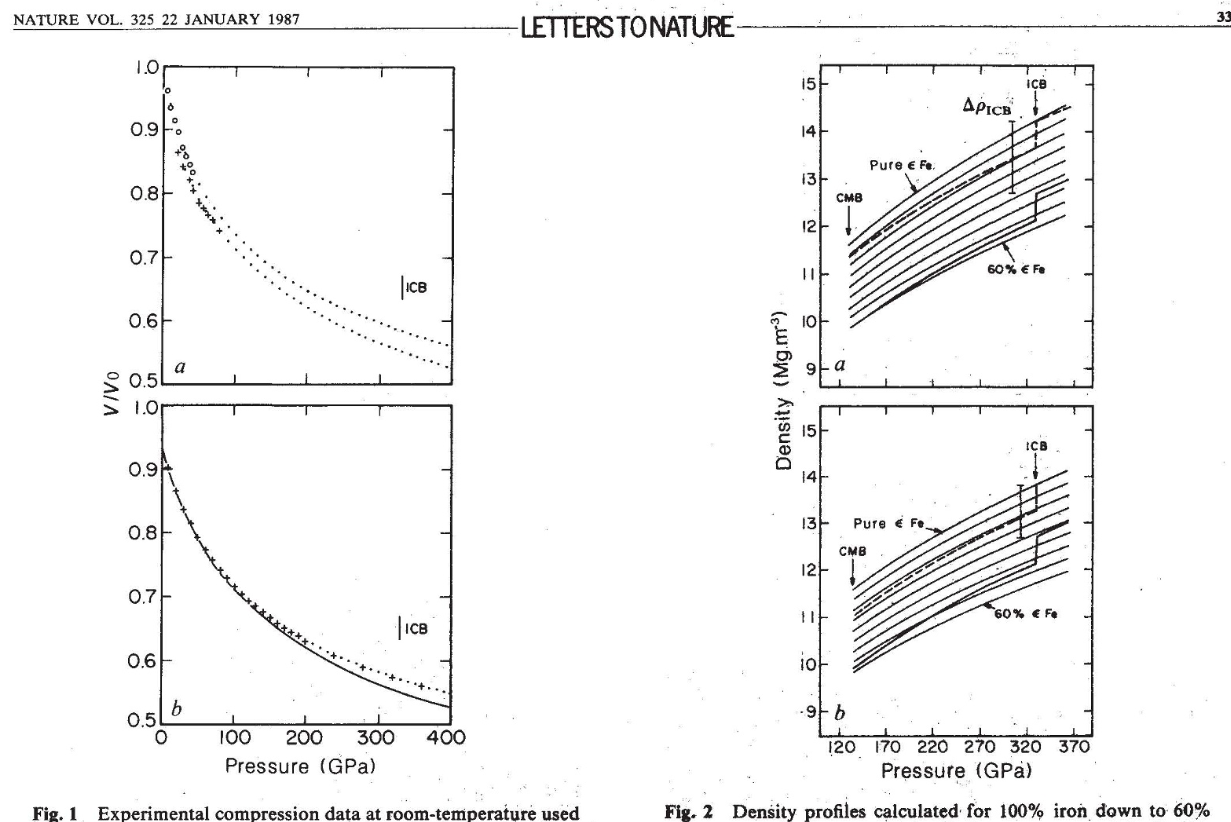
（固体体积和密度和压强的关系，来自1987年发表的论文。在地球内部，压强很大，物质的密度也很大）

注：这个问题是高中物理竞赛题的一个改版。在物理竞赛中有一个很有名的题目，即如果一个隧道穿越地球，计算一个物体自由落体运动的周期。其关键点在于，随着深度不同，重力加速度$g(r)$也不同。这个题目也是根据凡尔纳的《地心游记》所设想出的一条假想隧道而设计出来的。本文的简单的估算，可以让我们对地球内部的性质有一个大概的了解，而所用的知识，无非是最简单的经典力学知识而已。