[敬请读者注意] 本人保留本文的全部著作权利。如果哪位读者使用本文所描述内容，请务必如实引用并明白注明本文出处。如果本人发现任何人擅自使用本文任何部分内容而不明白注明出处，恕本人在网上广泛公布侵权者姓名。敬请各位读者注意，谢谢！

悖论集锦(2) –- 作为逻辑学中最大难题的蕴涵悖论问题（下） 

程京德

“逻辑学是一门研究论证与推理之正确性的基础性学问，其目的为建立和建全用于判断各种论证与推理之正确性的一般标准。”[1]  “逻辑学是最最重要的学问，没有任何其它学问比逻辑学更重要，因为逻辑学是任何其它学问之基础。”[2] “逻辑学之古老的、有趣的、有效的用途之一就是用来辨识、分析、解决各种悖论问题。”[3] “但是，实际上，逻辑学自身也有悖论！” “只要任何逻辑系统中被发现有与我们人类思维直觉相悖的‘悖论’问题，那么，我们就应该并且也必须去解决它们，这是逻辑学作为最最基本的规范性学问义不容辞的‘学科责任’！” [3] 

实质蕴涵悖论的解决方案 – 严格蕴涵及现代模态逻辑 

因为刘易斯在二十世纪初提出并定义了“严格蕴涵(strict implication)”概念并且构造了一系列最初的现代模态逻辑系统，所以通常被逻辑学界认为是现代模态逻辑的创始人 [81,89-102]；而作为现代模态逻辑的先驱，麦柯尔在十九世纪末二十世纪初就明确地提出了用模态概念“必然”来定义作为条件句表达的“蕴涵”；有逻辑学家考证，麦柯尔的模态逻辑系统等价于现代模态逻辑系统T [69,77-81]。

实际上，受到麦柯尔的影响，刘易斯的工作的最初目的就是改造经典数理逻辑里的实质蕴涵，试图找到一个可以替代实质蕴涵的新逻辑联结词来更准确地表达条件句 [81,89-102]。刘易斯认为，实质蕴涵的问题在于没有表达出条件句中的必然性，因此他引入了表达“不可能”的模态算子“~”来定义被用来表达条件句的蕴涵关系，并称之为“严格蕴涵”（刘易斯用“-3”[俗称“刘易斯鱼钩”]来表达）: A-3B =_df~(Aand notB)，并且构造了以“严格蕴涵”为原始联结词(primitive connective)的模态逻辑系统 S1,S2,S3,S4,S5[81,89-102]。

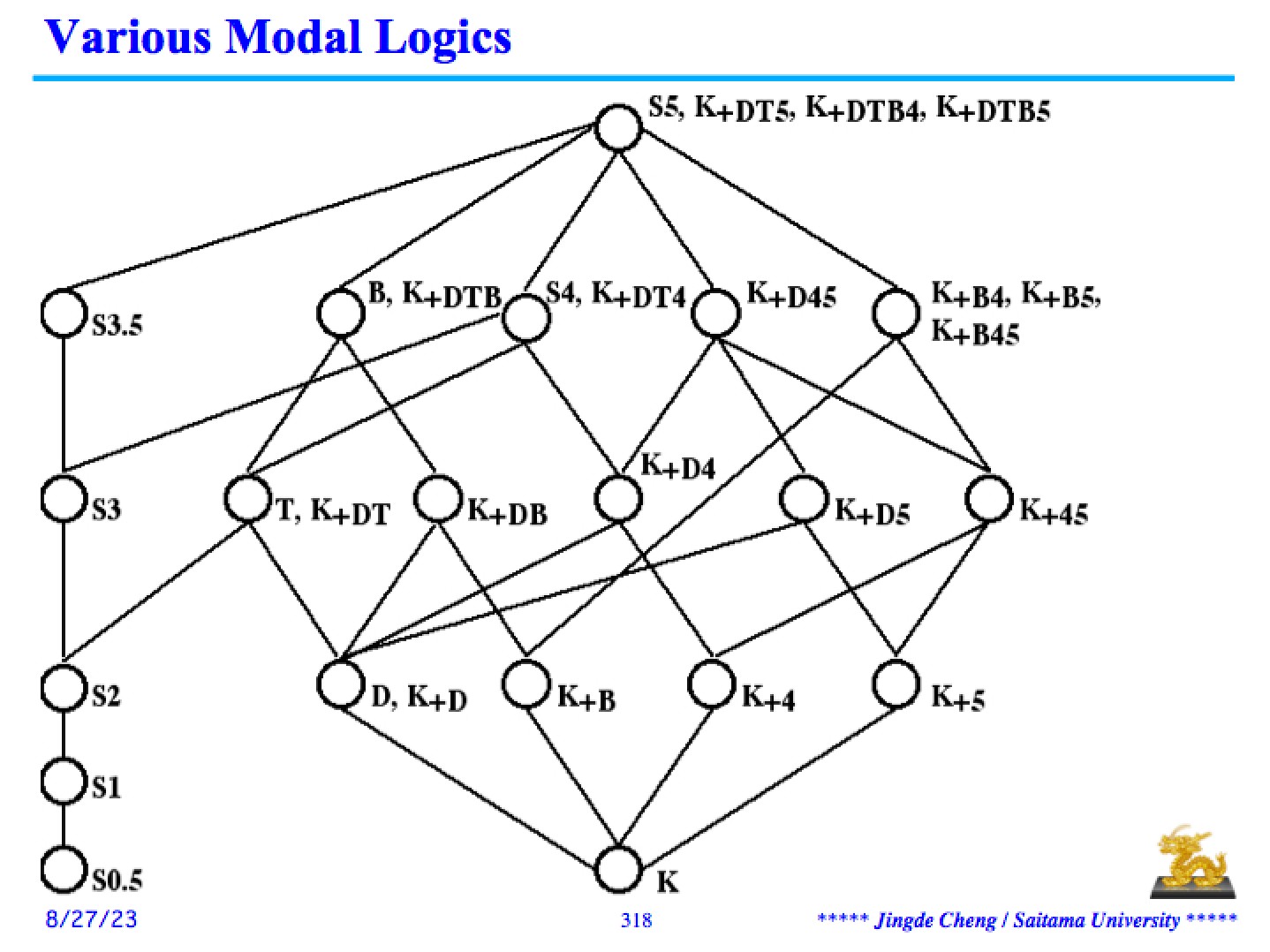
如果用现代模态逻辑表达“必然”的模态算子“□”和表达“可能”的模态算子“◇”来定义“严格蕴涵”，那么则为: A-3B =_df□(A->B), A-3B =_dfnot◇(Aand notB)[97-102]。所有的规范模态逻辑系统（包括刘易斯的S4和S5，但是不包括 S1,S2,S3）都是经典数理逻辑的保存扩张；如果在目标语言中添加模态算子，在演绎系统中添加推理规则必然化规则，并且添加若干公理，那么依照在规范模态逻辑系统的逻辑定理集合之间的偏序关系，各个规范模态逻辑系统形成如下图所示的偏序格 [97-102]。

因为在刘易斯的模态逻辑系统中，“严格蕴涵”是被用来表达条件句的原始联结词，并且推理规则分离规则(Modus Ponens)中用来表达条件句的也是“严格蕴涵”，实质蕴涵仅仅不过是可以用“否定”及“联言”或者用“否定”及“选言”定义的一个真值函数，所以，经典数理逻辑里那些实质蕴涵悖论在刘易斯的模态逻辑系统中就不再可以被视为表达有效推理的逻辑定理了，亦即，被刘易斯的模态逻辑系统排除掉了。请注意，如果在规范模态逻辑中，“实质蕴涵”被用来表达条件句的原始联结词，并且推理规则分离规则(Modus Ponens)中用来表达条件句的也是“实质蕴涵”的话，那么所有的规范模态逻辑系统都是经典数理逻辑的保存扩张，所以，并不能说实质蕴涵悖论被规范模态逻辑排除掉了。

尽管实质蕴涵悖被刘易斯的模态逻辑系统排除掉了，但是在刘易斯的几个模态逻辑系统当中，仍然遗留了一些“严格蕴涵悖论(paradoxes of strict implication)”[4-23,68,81,103-105]，比如：

□A->(B-3A)[相当于经典数理逻辑中的 A->(B->A)] 

□notA->(A-3B) [相当于经典数理逻辑中的 notA->(A->B)] 

(notA and A)-3B [相当于经典数理逻辑中的 (notA and A)->B] 

B-3(notA or A) [相当于经典数理逻辑中的 B->(notA or A)] 

刘易斯模态逻辑中的严格蕴涵悖论，(notA and A)-3B 和 B-3(notA or A)，以和经典数理逻辑中的实质蕴涵悖论，(notA and A)->B 和 B->(notA or A)，完全相同的形式出现，故而被一些逻辑学家称为最典型最难排除的蕴涵悖论。

在这两类蕴涵表达式（(notA and A)->B和B->(notA or A)，(notA and A)-3B 和 B-3(notA or A)）中，蕴涵之前件与后件之间可以不共享任何命题变量，因此可以是绝对毫不相干的。那么，按照我们前面对“蕴涵悖论”的一般性定义（“如果一个条件句的蕴涵表达式中，条件句的前件和后件之间不存在有必然的相关关系，那么我们称这样的蕴涵表达式为‘蕴涵悖论’”），这两类蕴涵表达式应该属于蕴涵悖论。

1955年，日本逻辑学家杉原丈夫提出了判别一个形式逻辑系统是否含有蕴涵悖论的第一个一般性判别标准：“对于含有蕴涵联结词的形式系统，如果逻辑式A被系统中的每个逻辑式所蕴涵，则A是最弱的公式；如果逻辑式A蕴涵每个逻辑式，则A是最强逻辑式。如果一个形式逻辑系统包含有最弱逻辑式或最强逻辑式，那么它就是含有蕴涵悖论的”[7]。 

依照杉原标准，因为经典数理逻辑和刘易斯模态逻辑都包含有最弱逻辑式(notA or A)和最强逻辑式(notA and A)，所以都是含有蕴涵悖论的。

实质蕴涵悖论和严格蕴涵悖论的解决方案 – 相关蕴涵及相关逻辑 

1956年，德国逻辑学家阿克曼(Wilhelm Ackermann,1896-1962)指出，用一个外延真值函数联结词来表达条件句是有问题的，应该用一个原始内涵联结词来表达条件句 [5,6]；这在逻辑学史上是一个极其具有革新性的思想，也是相关逻辑这个领域的发端 [5-23]。

阿克曼提出一个新的内涵逻辑联结词，称为“Strengen Implikation(rigorous implication,严密蕴涵)”（在本文中用“=>”来表达），用其来表达条件句，并且说到，“严密蕴涵，我们写为“A=>B”，应该表达这样一个事实： 在A和B之间存在有一种逻辑联系，B的内容是A的内容的一部分。这与A或B的假真无关。因此，人们会拒绝逻辑式A=>(B=>A)的有效性，因为它允许从A推出 B=>A，而A的真值与B和A之间是否存在有逻辑联系无关。(Rigorous implication, which we write as A=>B, should express the fact that a logical connection holds between A and B, that the content of B is part of that of A, or however one wishes to express it.  That has nothing to do with the truth of falsity of A or B.  Thus one would reject the validity of the formula A=>(B=>A), since it permits the inference from A of B=>A, and since the truth of A has nothing to do with whether a logical connection holds between B and A.)”[5,7,22]。阿克曼提出的对表达条件句的原始内涵逻辑联结词的思想，后又被 von Wright，Geach，Smiley 三位逻辑学家分别归纳和陈述，现在被称为“The von-Wright-Geach-Smiley criterion for entailment”，简称“WGS criterion”，是关于条件句表达的重要标准 [7]。

阿克曼构筑了以“严密蕴涵”为初始内涵联结词的形式逻辑系统π',这是逻辑学史上第一个完整的相关逻辑系统。π’从其逻辑定理中成功地完全排除了实质蕴涵悖论和严格蕴涵悖论 [5,6]。

美国逻辑学家安德森(Alan Ross Anderson)和贝尔纳普(Nuel Dinsmore Belnap, Jr.)以及他们的学生们从上世纪五十年代到七十年代在相关逻辑领域做了一系列的工作。他们提出了原始内涵联接词“必然归结(entailment)”的概念，并且将阿克曼的相关逻辑π’重构为等价的相关逻辑系统“system E of entailment”，提出了原始内涵联接词“相关蕴涵(relevant implication)”的概念并构造了相关逻辑系统“system R of relevant implication”（以及其它一些相关逻辑系统）[7-23]。这些相关逻辑系统都从其逻辑定理中成功地完全排除了实质蕴涵悖论和严格蕴涵悖论 [7-23]。

各个相关逻辑系统完全排除实质蕴涵悖论和严格蕴涵悖论的理论保证源于“相关性原理(The relevance principle)”：一个条件句形式的相关逻辑定理之前件与后件之间必然共享至少一个命题变量。相关性原理在形式上保证了在相关逻辑中作为逻辑定理的条件句命题的前件与后件之间的必然相关性，这正是所有相关逻辑系统必然满足的本质特征 [7-23]。正是因为所有相关逻辑系统的逻辑定理都必然地满足相关性原理，其条件句形式逻辑定理的前件后件之间都共享至少一个命题变量，所以那些前件与后件之间毫不相关的、被称之为最典型最难排除的蕴涵悖论就都被从相关逻辑系统中排除掉了。

然而，是否严密蕴涵、必然归结、相关蕴涵已经完美地准确表达了充分条件关系，相关性原理已经完美地限制了所有的蕴涵悖论，传统的相关逻辑已经彻底解决了条件句表达这一难题了呢？如果依照本文前面给出的“蕴涵悖论”之一般性定义（“如果一个条件句的蕴涵表达式中，条件句的前件和后件之间不存在有必然的相关关系，那么我们称这样的蕴涵表达式为‘蕴涵悖论’”），那么显然，满足相关性原理的相关逻辑已经排除掉“全部”蕴涵悖论，似乎可以说蕴涵悖论问题已经解决了。但是，如同我们已经提及的，上述“蕴涵悖论”之一般性定义并未覆盖到“相关蕴涵悖论”。

相关蕴涵悖论及其解决方案

由于相关性原理仅仅要求在一个条件句形式相关逻辑定理的前件与后件之间必须共享至少一个命题变量，它仅仅保证了该条件句的前件后件之间的必然相关，却没有保证前件中的所有成分与后件中的所有成分都必然相关。因此，在一个条件句形式相关逻辑定理中，其前件可能会含有与后件毫不相干的成分，或者其后件可能会含有与前件毫不相干的成分。

让我们来考虑下面几个例子：

(A and B)=>A, 

(A and B and …)=>A, 

(A and B)=>B, 

(A and B and …)=>B, 

(A and B)=>((A and C)=>B), 

(A and B)=>((A and C and …)=>B) 

这些条件句形式命题都是相关逻辑的逻辑定理（都满足相关性原理），因此把具体命题代入其命题变量都应该得到（在相关逻辑系统内的）真命题。但是，在这些逻辑定理的前件中都包含有与后件不相关的合取項。比如，把具体命题“雪是白的”，“1+1=2”，“1+1=3”代入命题变量A，B，C，那么会得到：

(雪是白的 and 1+1=2)=>雪是白的，

(雪是白的 and 1+1=2 and …)=>雪是白的，

(雪是白的 and 1+1=2)=>1+1=2，

(雪是白的 and 1+1=2 and …)=>1+1=2，

(雪是白的=>1+1=2)=>((雪是白的 and 1+1=3) =>1+1=2)，

(雪是白的=>1+1=2)=>((雪是白的 and 1+1=3 and …)=>1+1=2)

显然，如果把上面这些例子中的相关的蕴涵联结词“=>”都视为充分条件关系“如果…，那么…”之表达，那么得到的条件句在含义上就很怪异可笑了，因为按照通常的常识和经验来看，这些条件句的前件里有一部分与后件毫不相干，甚至即便某些成分是假命题或者后件之否定也无妨。

让我们再考虑下面几个例子：

A=>(A or B), 

A=>(A or B or …), 

B=>(A or B), 

B=>(A or B or …), 

(A=>B)=>(A=>(B or C)), 

(A=>B)=>(A=>(B or C or …)) 

这些条件句形式命题也都是相关逻辑的逻辑定理（都满足相关性原理），因此把具体命题代入其命题变量也都应该得到（在相关逻辑系统内的）真命题。但是，在这些逻辑定理的后件中都包含有与前件不相关的析取项。如果把具体命题“雪是白的”，“1+1=2”，“1+1=3”代入命题变量A，B，C，也会得到在含义上很怪异可笑的条件句。

从这些实例可以看出，尽管传统相关逻辑已经排除了那些传统的实质蕴涵悖论及严格蕴涵悖论，但是在它们的逻辑定理集合当中也还仍然存在着一些条件句形式逻辑定理，从我们通常使用充分条件关系的意义来看是不自然的、怪异可笑的。如果将传统相关逻辑中的相关蕴涵联结词就视为是充分条件关系，而把相关逻辑中的逻辑定理都视为有效的推理形式，那么从正确推理的角度来看，传统相关逻辑的许多逻辑定理仍然表现出类似于“实质/严格蕴涵悖论”的特性。这一情形，与把经典数理/模态逻辑中的“实质/严格蕴含”视为是充分条件关系，而把经典数理/模态逻辑中的逻辑定理都视为有效的推理形式时所产生的“实质/严格蕴含悖论”问题完全类似。这个事实揭示了，尽管“相关蕴涵”比“实质/严格蕴涵”更恰当地表达了充分条件关系概念，但是类似于“实质/严格蕴涵”的情形，“相关蕴涵”也还没有完美地准确表达充分条件关系  [106,107]。

笔者于上世纪90年代前期发现并指出了传统相关逻辑中的上述问题，命名相关逻辑系统中的那些有问题的逻辑定理为“合取蕴涵悖论(conjunction-implicational paradox)”和“析取蕴涵悖论(disjunction-implicational paradox)”[106,107]。在一个合取蕴涵悖论的前件中包含有不必要的、不需要的、不相干的合取项，在一个析取蕴涵悖论的后件中包含有不必要的、不需要的、不相干的析取项，或者两者皆而有之。

为了建立起能够支持相关推论的条件句逻辑演算，笔者提出了排除合取蕴含悖论和析取蕴含悖论的强相关逻辑（strong relevant logic, strong relevance logic）系统。强相关逻辑要求，对于每一个表示有效的推理形式的条件句形式逻辑定理来说，其前件中不得包含不必要的、不需要的、不相干的合取项，并且其后件中不得包含不必要的、不需要的、不相干的析取项。强相关逻辑在相关逻辑满足相关性原理的基础上，进一步满足“强相关性原理(The strong relevance principle)”：“条件句形式逻辑定理中的每一个命题变量必须作为前件成分和后件成分各出现至少一次”。作为传统相关逻辑的改良，强相关逻辑排除了传统相关逻辑中的合取蕴含悖论和析取蕴含悖论，使得在一个基于满足强相关性原理的强相关逻辑的有效推论之前提中不会出现与其结论无关的合取项，结论中也不会出现与其前提无关的析取项[106,107]。

如前所述，本文前面给出的“蕴涵悖论”之一般性定义（“如果一个条件句的蕴涵表达式中，条件句的前件和后件之间不存在有必然的相关关系，那么我们称这样的蕴涵表达式为‘蕴涵悖论’”）并未覆盖到“相关蕴涵悖论”。如何更一般地定义蕴涵悖论？强相关逻辑中是否还遗留有其它蕴涵悖论？强相关逻辑中的“强相关蕴涵”是否已经恰如其分地表达了条件句？这些还都是未解决的问题。

结语：完全解决蕴涵悖论问题的重要意义 

本文至此已经介绍了蕴涵悖论问题的历史背景和现状，可以说，蕴涵悖论问题至今还未完全解决，还需要继续调查和研究。那么，完全解决蕴涵悖论问题的重要意义何在？

从逻辑学来说，如果把条件句视为逻辑学的最核心概念，那么条件句概念的清晰准确定义，条件句概念在形式逻辑系统中的清晰准确表达，就是逻辑学中最大的难题 [4]。可以说，没有蕴涵悖论问题的完全解决，就不会有条件句概念的清晰准确定义和表达。如同笔者多次强调的，完全解决蕴涵悖论问题是逻辑学作为最最基本的规范性学问义不容辞的‘学科责任’！[3] 

从逻辑学的应用来说，哲学、数学、自然科学、社会科学，都需要逻辑学的基础支撑，条件句在所有（没有例外）的文学、哲学、社会科学、逻辑学、数学、自然科学、工程技术等各个领域以及我们人类日常生活言谈交流中都起到必不可少、不可或缺的基本作用，条件句概念的清晰准确定义和表达当然就是极其重要的。

以当下在全世界最热的人工智能领域为例。笔者个人的观点是，逻辑学及其应用还并未被人工智能领域的研究工作者准确清晰地认识清楚，其原因就是逻辑学自身还未能为人工智能领域提供足够的基础理论支撑。美国计算机科学家 Newell(A. Newell, 1927-1992, 1975年图灵奖获得者), Shaw(J.C. Shaw, 1922-1991) 和 Simon(H.A. Simon, 1916-2001, 1975年图灵奖获得者, 1978 年诺贝尔经济学奖获得者)在 1955-1956 年开发了一个称为“逻辑理论家(Logic Theorist)”的自动演绎证明程序（被称为第一个真正的人工智能程序），自动地判定一个给定经典命题演算命题的真伪 [108]。逻辑理论家成功地自动证明了怀德海和罗素的名著“PM”中命题演算部分的 38 个定理 [108-110]。华裔美国逻辑学家王浩(H. Wang, 1921-1995)在 1958 年用汇编语言开发了三个针对经典一阶谓词演算的自动演绎证明程序，在 IBM704 计算机上用不到 9 分钟的计算时间自动证明了“PM”中一阶谓词演算部分的全部定理（350条以上）[67,111]。逻辑理论家和王浩的自动演绎证明程序是基于经典数理逻辑工作的，结果，从那时开始时至今日，在人工智能领域，众多人士把经典数理逻辑的局限性（尤其是蕴涵悖论问题）认为是逻辑学的局限性，尽管现代模态逻辑及相关逻辑早已突破了经典数理逻辑的局限性。近年来，伴随着对实现人工通用智能(AGI)的期待，为人工智能寻求和建立统一的一般基础理论的呼声越来越高。笔者相信，人工智能的统一的一般基础理论一定是建立在完全解决了蕴涵悖论问题的逻辑理论之上的。 

参考文献

[1] 程京德，“逻辑学是什么”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年1月25日。

[2] 程京德，“逻辑学之重要性（及对其在中国被轻视之原因初探）”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年1月27日。

[3] 程京德，“悖论集锦 (1) -- 逻辑学中也有悖论意味着什么？”微信公众号“数理逻辑与哲学逻辑”，科学网博客，2024年1月20日，“悖论集锦 (1) -- 逻辑学中也有悖论意味着什么？”（增补版），微信公众号“数理逻辑与哲学逻辑”，2024年1月25日。

[4] 程京德，“条件句：逻辑学中的最核心概念及最大难题”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年1月29日。

[5] W. Ackermann, “Begrundung Einer Strengen Implikation,” The Journal of Symbolic Logic, Vol. 21, pp. 113-128, 1956 (in German). 

[6] D. Hilbert and W. Ackermann, “Grundzuge der theoretischen Logik,” 4 Auflage, Springer-Verlag, 1959, 6 Auflage, Springer-Verlag, 1972 (in German). [Ackermann added a section about his work on relevant logic in the 4th edition of this book.] 

[7] A. R. Anderson and N. D. Belnap Jr., “Entailment: The Logic of Relevance and Necessity,” Vol. I, Princeton University Press, Princeton, 1975. 

[8] A. R. Anderson， N. D. Belnap Jr., and J. M. Dunn, “Entailment: The Logic of Relevance and Necessity,” Vol. II, Princeton University Press, Princeton, 1992. 

[9] M. R. Diaz, “Topics in the Logic of Relevance,” Philosophia Verlag, Munchen, 1981. 

[10] R. Routley, V. Plumwood, R. K. Meyer, and R. T. Brady, “Relevant Logics and Their Rivals, Part I, The Basic Philosophical and Semantical Theory,” Ridgeview, Atascadero, California, 1982. 

[11] R. Brady (Ed.), “Relevant Logics and Their Rivals, Volume II, A Continuation of the Work of Richard Sylvan, Robert Meyer, Val Plumwood, and Ross Brady,” Ashgate Publishing, Aldershot, 2003. 

[12] J. Norman and R. Sylvan (Eds.), “Directions in Relevant Logic,” Kluwer Academic, Dordrecht, 1989. 

[13] S. Read, “Relevant Logic: A Philosophical Examination of Inference,” Basil Blackwell, Oxford, 1988, 2012. 

[14] E. D. Mares, “Relevant Logic: A Philosophical Interpretation,” Cambridge University Press, Cambridge, 2004. 

[15] G. Priest, “An Introduction to Non-Classical Logic - From If to Is, Second Edition,” Part I Propositional Logic - Chapter 1 Classical Logic and the Material Conditional, Part I Propositional Logic - Chapter 10 Relevant Logics, Part II Quantification and Identity - Chapter 24 Relevant Logics, Cambridge University Press, Cambridge, 2008. 

[16] J. M. Dunn, “Relevance Logic and Entailment,” in D. Gabbay and F. Guenthner (eds.), “Handbook of Philosophical Logic,” Vol. III, pp. 117-224, D. Reidel, Dordrecht, 1986. 

[17] J. M. Dunn and G. Restall, “Relevance Logic,” in D. Gabbay and F. Guenthner (Eds.), “Handbook of Philosophical Logic, 2nd Edition,” Vol. 6, pp. 1-128, Kluwer Academic, Dordrecht, 2002. 

[18] E. D. Mares and R. K. Meyer, “Relevant Logics,” in L. Goble (Ed.), “The Blackwell Guide to Philosophical Logic,” pp. 280-308, Blackwell, Oxford, 2001. 

[19] E. D. Mares, “Relevance Logic,” in D. Jacquette (Ed.), “A Companion to Philosophical Logic,” pp. 609-627, Blackwell, Oxford, 2002. 

[20] G. Restall, “Relevant and Substructural Logics,” in D. M. Gabbay and J. Woods (Eds.), “Handbook of the History of Logic,” Vol. 7, Elsevier B.V., Amsterdam, 2006. 

[21] K. Bimbo, “Relevance Logics,” in D. Jacquette (Ed.), “Philosophy of Logic,” pp. 723-789, Elsevier B. V., Amsterdam, 2007. 

[22] A. Aberden and S. Read， “Philosophy of Alternative Logics,” in L. Haaparanta (Ed.), “The Development of Modern Logic,” Oxford University Press, Oxford, 2009.

[23] E. D. Mares, “Relevance Logic,” The Stanford Encyclopedia of Philosophy, Center for the Study of Language and Information (CSLI), Stanford University, 1998, 2020. 

[24] D. Edgington, “Indicative Conditionals,” The Stanford Encyclopedia of Philosophy, Center for the Study of Language and Information (CSLI), Stanford University, 2001, 2020. 

[25] F. von Kutschera, “Indicative Conditionals,” Theoretical Linguistics, Vol. 1, pp. 257-269, 1974. 

[26] E. C. Traugottet al. (Eds), “On Conditionals,” Cambridge University Press, Cambridge, 1986. 

[27] F. Jackson, “Conditionals,” Basil Blackwell, Oxford, 1987. 

[28] F. Jackson (Ed.), “Conditionals,” Oxford University Press, Oxford, 1991.

[29] G. Crocco et al. (Eds.), “Conditionals: From Philosophy to Computer Science,” Clarendon Press, Oxford, 1995.

[30] D. Edgington, “On Conditionals,” Mind, Vol. 104, pp. 235-329, 1995. 

[31] M. Woods, “Conditionals,” Clarendon Press, Oxford, 1997. 

[32] D. Edgington, “Conditionals,” in L. Goble (Ed.), The Blackwell Guide to  Philosophical Logic, Blackwell, Oxford, 2001.

[33] D. H. Sanford, “If P, Then Q: Conditionals and the Foundations of Reasoning, Second Edition,” Routledge, London and New York, 1989, 2003. 

[34] J. Bennett, “A Philosophical Guide to Conditionals,” Clarendon Press, Oxford， 2003.

[35] A. S. Gillies, “Epistemic Conditionals and Conditional Epistemics,” Noûs, Vol. 38, No. 4, pp. 585-616, 2004.

[36] N. Rescher, “Conditionals,” MIT Press, Cambridge, 2007. 

[37] Kai von Fintel, “Conditionals,” in K. von Heusinger, C. Maienborn, and P. Portner (Eds.), “Semantics: An International Handbook of Meaning,” Mouton De Gruyter, 2011. 

[38] R. Declerckand S. Reed, “Conditionals: A Comprehensive Empirical Analysis,” Walter de Gruyter, 2012. 

[39] W. L. Harper, G. A. Pearce, and R. Stalnaker, “IFS: Conditionals, Belief, Decision, Chance and Time,” Springer, 2012. 

[40] M. Mandelkern, “If P Then P!” The Journal of Philosophy, Vol. 118, Issue 12, pp. 645-679, 2021. 

[41] L. Walters and J. Hawthorne (Eds.), “Conditionals, Paradox, and Probability: Themes from the Philosophy of Dorothy Edgington,” Oxford University Press, Oxford, 2021. 

[42] S. Kaufmann, D. E. Over, and G. Sharma, “Conditionals: Logic, Linguistics and Psychology,” Springer, 2023. 

[43] W. B. Starr, “Counterfactuals,” The Stanford Encyclopedia of Philosophy, Center for the Study of Language and Information (CSLI), Stanford University, 2019. 

[44] A. R. Anderson, “A Note on Subjunctive and Counterfactual Conditionals.” Analysis, Vol. 11, pp. 35-38, 1951. 

[45] E. W. Adams, “Subjunctive and Indicative Conditionals,” Foundations of Language, Vol. 6, No. 1, pp. 89-94, 1970. 

[46] D. K. Lewis, “Counterfactuals,” Blackwell, Oxford, 1973. 

[47] F. Jackson, “Classifying Conditionals,” Analysis, Vol. 50, No. 2, pp. 134-147, 1990. 

[48] B. Weatherson, “Indicative and Subjunctive Conditionals,” Philosophical Quarterly, Vol. 51 pp. 200-216, 2001.

[49] T. Williamson, “Indicative versus Subjunctive Conditionals, Congruential versus Non-Hyperintensional Contexts,” Philosophical Issues, Vol. 16, 2006. 

[50] G. Gomes, “Three Types of Conditionals and Their Verb Forms in English and Portuguese,” Cognitive Linguistics, Vol. 19, No. 22, pp. 219–240, 2008. 

[51] K. von Fintel, “Subjunctive Conditionals,” in G. Russell and D. G. Fara  (Eds.), “The Routledge Companion to Philosophy of Language,” Routledge, New York， 2012. 

[52] M. Ippolito, “Subjunctive Conditionals: A Linguistic Analysis,” MIT Press, Cambridge, 2013. 

[53] J. Khoo, “On Indicative and Subjunctive Conditionals,” Philosophers' Imprint, Vol. 15, No. 32, pp. 1-40, 2015. 

[54] P. Egre and H. Rott, “The Logic of Conditionals,” The Stanford Encyclopedia of Philosophy, Center for the Study of Language and Information (CSLI), Stanford University, 2021. 

[55] E. Adams, “The Logic of Conditionals,” Inquiry: An Interdisciplinary Journal of Philosophy, Vol. 8, Issue 1-4, pp. 166-197, 1965. 

[56] E. W. Adams, “The Logic of Conditionals: An Application of Probability to Deductive Logic,” D. Reidel, Dordrecht, 1975. 

[57] W. B. Starr, “A Uniform Theory of Conditionals,” Journal of Philosophical Logic, Vol. 43, pp. 1019-1064, 2014. 

[58] S. Haack, “Philosophy of Logics,” Cambridge University Press, Cambridge, 1978. 

[59] S. Read, “Thinking About Logic - An Introduction to the Philosophy of Logic,”Oxford Unversity Press, Oxford, 1995. 

[60] I. M. Copi and C. Cohen, “Introduction to Logic,” 1953, 1961 (I. M. Copi), 1968, 1972, 1978, 1982, 1986, 1990, 1994, 1998, 2002, 2005, 2008 (I. M. Copi and C. Cohen), Routledge, 2011 (with K. D. McMahon) (14th Edition), 2018 (with V. Rodych) (15th Edition). 

[61] P. J. Hurley, “A Concise Introduction to Logic,” Wadsworth, 1982, 1985, 1988, 1991, 1993, 1997, 1999, 2003, 2005, 2008, Cengage Learning, 2012, 2014, 2016 (with L. Watson) (13th Edition). 

[62] W. Kneale and M. Kneale, “The Development of Logic,” Clarendon Press, Oxford,  1962, 1984 (Paperback Edition with Corrections); 《逻辑学的发展》（张家龙,洪汉鼎 译），商务印书馆, 1985. 

[63] N. Rescher, “Avicenna on the Logic of ‘Conditional’ Propositions,” Notre Dame Journal of Formal Logic, Vol. IV, No. 1, pp. 48-58, 1963. 

[64] R. Strobino, “Ibn Sina’s Logic,” The Stanford Encyclopedia of Philosophy, Center for the Study of Language and Information (CSLI), Stanford University, 2018. 

[65] S. Chatti, “Avicenna (Ibn Sina): Logic,” The Internet Encyclopedia of Philosophy.  

[66] J. van Heijenoort (Ed.), “From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931,” Harvard University Press, Cambridge, Massachusetts, 1967. 

[67] 王浩，“数理逻辑通俗讲话” [第一章为数理逻辑100年]，科学出版社，1981.

[68] 王宪钧, “数理逻辑引论” [第三篇为数理逻辑发展简述]，北京大学出版社，1982, 1998. 

[69] 张家龙，“数理逻辑发展史 - 从莱布尼茨到哥德尔”，社会科学文献出版社，1993.

[70] F. L. G. Frege, “Begriffsschrift(a formulalanguage, modeled on that of arithmetic, for pure thought),”1879. 

[71] G. Peano, “Arithmetices Principia: Nova Methodo Exposita(The Principles of Arithmetic, Presented by a New Method),” 1889. 

[72] B. Russell, “Towards the “Principles of Mathematics”, 1900-1902,” in G. H. Moore (Ed.), “The Collected Papers of Bertrand Russell,” Vol. 3, Routledge, London, 1993. 

[73] B. Russell, “The Principles of Mathematics”, George Allen & Unwin Ltd, London, 1903.  

[74] A. N. Whitehead and B. A. W. Russell, “Principia Mathematica,” Vol.1, 1910(1 ed.), 1925(2 ed.), Vol.2, 1912(1 ed.), 1927(2 ed.), Vol.3, 1913(1 ed.), 1927(2 ed.), Cambridge University Press. 

[75] H. MacColl, “Symbolical Reasoning,” Mind, Vol. 5, No. 17, pp. 45-60, 1880. 

[76] H. MacColl, “Symbolic Logic and Its Application,” Longmans, Green, & Co., London, 1906. 

[77] S. Rahmanand J. Redmond, “Hugh MacColl - An Overview of His Logical Work With Anthology,” College Pubns, 2007 [This book includes a reprint of MacColl's main writings on logic].

[78] S. Read, “Hugh MacColl and the Algebra of Strict Implication,” in M. Astroh and S. Read (Eds.), “Hugh MacColl and the Tradition of Logic,” Nordic Journal of Philosophical Logic, Vol. 3, No. 1, pp. 59-83, 1998. 

[79] M. Astroh and S. Read, “A Survey of the Life of Hugh MacColl (1837-1909),” in A. Moktefi and S. Read (dir.), “Hugh MacColl after One Hundred Years,” Philosophia Scientiæ, Vol. 15, No. 1, pp. 7-29, 2011. 

[80] R. Ballarin, “Modern Origins of Modal Logic,”The Stanford Encyclopedia of Philosophy, Center for the Study of Language and Information (CSLI), Stanford University, 2010, 2021. 

[81] 周礼全，“模态逻辑引论” [第十一章为模态逻辑简史]，上海人民出版社，1986.

[82] “Paradoxes of Material Implication,” The Oxford Dictionary of Philosophy. 

[83] J. L. Mackie “Truth, Probability and Paradox,” Oxford University Press, 1973. 

[84] R. Brandom, “Semantic Paradox of Material Implication,”Notre Dama Journal of Formal Logic, Vol. 22, No. 2, pp. 129-132, 1981.  

[85] C. R. Ceniza, “Material Implication and Entailment,”Notre Dama Journal of Formal Logic, Vol. 29, No. 4, pp. 510-519, 1988.  

[86] D. K. Johnston, “The Paradox of Indicative Conditionals,” Philosophical Studies, Vol. 83, pp. 93-112, 1996. 

[87] F. Paoli, “Implicational Paradoxes and the Meaning of Logical Constants,” Australasian Journal of Philosophy, Vol. 85, Issue 4, pp. 553-579, 2007. 

[88] S. Reza, “Material Implication, Paradox of Material Implication and its Criticism,” SSRG International Journal of Humanities and Social Science, Vol. 9, Issue 5, pp. 25-29, 2022. 

[89] C. I. Lewis, “Implication and the Algebra of Logic”, Mind, Vol. 21, No. 84, pp. 522-531, 1912. 

[90] C. I. Lewis, “The Calculus of Strict Implication”, Mind, Vol. 23, No. 1, pp. 240-247, 1914. 

[91] C. I. Lewis, “The Issues Concerning Material Implication”, Journal of Philosophy, Psychology and Scientific Methods, Vol. 13, Issue 14, pp. 350-356, 1917. 

[92] C. I. Lewis, “A Survey of Symbolic Logic,” University of California Press, Berkeley, 1918.

[93] C. I. Lewis, “Strict Implication - An Emendation”, Journal of Philosophy, Psychology and Scientific Methods, Vol. 17, Issue 11, pp. 300-302, 1920. 

[94] C. I. Lewis and C. H. Langford, “Symbolic Logic,” Century, London, 1932; 2nd Edition, Dover, New York, 1959. 

[95] E. Dayton, “Clarence Irving Lewis (1883—1964),” The Internet Encyclopedia of Philosophy.

[96] B. Hunter, “Clarence Irving Lewis,” The Stanford Encyclopedia of Philosophy, Center for the Study of Language and Information (CSLI), Stanford University, 2007, 2021. 

[97] J. Garson, “Modal Logic,” The Stanford Encyclopedia of Philosophy, Center for the Study of Language and Information (CSLI), Stanford University, 2000, 2023. 

[98] G. E. Hughes and M. J. Cresswell, “An Introduction to Modal Logic,” Methuen, London, 1968. 

[99] G. E. Hughes and M. J. Cresswell, “A Companion to Modal Logic,” Methuen, London, 1984.

[100] G. E. Hughes and M. J. Cresswell, “A New Introduction to Modal Logic,” Routledge, London, 1996. 

[101] B. F. Chellas, “Modal Logic - A Introduction,” Cambridge University Press, Cambridge, 1980. 

[102] 程京德，“哲学逻辑(2) – 模态逻辑”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年8月30日。

[103] T-C. Tang, “A Paradox of Lewis’s Strict Implication,” Bulletin of the American Mathematical Society, Vol. 42, pp. 707-709, 1936. 

[104] J. H. Woods, “Non-Paradoxical Paradoxes?” Notre Dame Journal of Formal Logic, Vol. 8, No. 4, pp. 346-352, 1967.

[105] I. Narita, “The Paradoxes of Strict Implication,” Logos Architekton. Journal of Logic and Philosophy of Science, Vol. 4, No. 1-2. pp. 61-72, 2010.

[106] 程京德，“相关推论与强相关逻辑”，科技导报，Vol. 34, No. 7, pp. 39-47, 2016. 

[107] 程京德，“强相关逻辑及其应用（上）、（中）、（下）”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年6月18日、2023年8月8日、2023年8月12日。

[108] A. Newell, J. Shaw, and H. Simon, “Empirical Explorations with the Logic Theory Machine,” in “Proceedings of West Joint Computer Conference,” pp. 218-239, 1957. 

[109] M. Davis, “The Early History of Automated Deduction,” in A. Robinson and A. Voronkov (Eds.), “Handbook of Automated Reasoning,” pp. 5-15, Elservier Science Publishers, 2001. 

[110] 程京德，“自动定理发现”，科学网博客，2015年2月23日。

[111] H. Wang, “Toward Mechanical Mathematics,” IBM Journal of Research and Development, Vol. 4, pp. 2-22, 1960.

微信公众号“数理逻辑与哲学逻辑”