博文
71、体温信号总体经验模式分解(eemd)研究(二)
|||
71、体温信号总体经验模式分解(eemd)研究(二)
上篇博文写了“体温信号总体经验模式分解”中,同时分解出组数最多的17Gimf。这篇看看其它情况。在分解出10000组17Gimf的同时时,分解组数第二的是16Gimf,大约为6000多组。由于不明原因,也许是误操作,丢失了大部分数据。剩下的数据稍加补充,凑成了一个整数2100组。看看它的总体合成imf各分量周期-能量情况:
figure(2);
W=1080;
H=720;
fg=figure(2);
set(fg,'position',[70,50,W,H]);
set(gca,'position',[0.035,0.06,0.95,0.88]);
hold on
aaimf=zeros(16,95196);
for i=1:210
aimf=zeros(16,95196);
for j=1:10
k=(i-1)*10+j;
imf=ST16(k).imf;%ST16为存有2100组16Gimf的结构变量
aimf=aimf+imf;
end
aimf=aimf/10;
AL(i).imf=aimf;
%下面计算该组aimf的正交指数
s = 0;
for j = 1:17
for k =1:17
if j~=k
fj=aimf(j,:);
fk=aimf(k,:);
fc=(fj*conj(fk)')/(x*x');
s = s + abs(fc);
end
end
end
AL(i).ort=s/2;
aort(i)=s/2;
aaimf=aaimf+aimf;
end
aaimf=aaimf/210;
AAL16.imf=aaimf;
for i=1:210
for j=1:15
imff=AL16(i).imf(j,:);
[mn,mx,ze]=extr(imff);
z9=ze(end);
z1=ze(1);
zl=length(ze);
zq=2*( z9-z1)/(zl-1);
AL16(i).zq(j)=zq;
nl=imff*imff';
AL16(i).nl(j)=nl;
plot(log(zq),log(nl),'.g')
end
end
title('十合2100合16Gimf各分量周期-能量图')
for j=1:15
imff=AAL16.imf(j,:);
[mn,mx,ze]=extr(imff);
z9=ze(end);
z1=ze(1);
zl=length(ze);
zqj=2*( z9-z1)/(zl-1);
zq(j)=zqj;
nlj=imff*imff';
nl(j)=nlj;
plot(log(zq),log(nl),'or')
plot(log(zq),log(nl),'hr')
end
AAL16.zq=zq;
AAL16.nl=nl;
%下面计算该组aaimf的正交指数
s = 0;
for j = 1:16
for k =1:16
if j~=k
fj=aaimf(j,:);
fk=aimf(k,:);
fc=(fj*conj(fk)')/(x*x');
s = s + abs(fc);
end
end
end
AAL16.ort=s/2;
aaort=s/2;
另外,原始(未加噪)的体温信号
x=TW793312的emd分解:
[imf0,ort0,v]=emd(x);
得到的是1组16Gimf。
for j=1:15
imff=imf0(j,:);
[mn,mx,ze]=extr(imff);
z9=ze(end);
z1=ze(1);
zl=length(ze);
zq=2*(z9-z1)/(zl-1);
zq0(j)=zq;
nl=imff*imff';
nl0(j)=nl;
figure(2)
hold on
plot(log(zq),log(nl),'xb')
end
如下图:

图71-1 十合2100合及原分析信号16Gimf各分量周期-能量图
首先可以看到,虽然同为16Gimf,但原始未加噪信号之imf各分量周期-能量点,与总体合成后的imf各分量周期-能量点的分布,有很大差距。说明emd的总体合成计算是及其必要的。
另外,十合、2100合16Gimf各分量的周期-能量点的聚散性,与17Gimf基本上是一样的。不多说。
其余剩下的14Gimf、15Gimf、18Gimf、19Gimf组数分别为10、781、1486、21组。统一将其叠加取均合成,各得1组imf。求各组及原始分析信号imf0、原万合17Gimf、2100合16Gimf各分量之周期、能量,得各组的周期向量zq0、zq14、zq15、zq16、zq17、zq18、zq19.,能量向量nl0、nl14、nl15、nl16、nl17、nl18、nl19。
绘zq-nl图:
figure(5);
W=1080;
H=720;
fg=figure(5);
set(fg,'position',[70,50,W,H]);
set(gca,'position',[0.035,0.06,0.95,0.88]);
hold on
zq=zq0;%zq14、zq15、zq16、zq17、zq18、zq19
nl=nl0;%nl14、nl15、nl16、nl17、nl18、nl19。
plot(log(zq),log(nl),'o--b')
title('不同分量个数的各合成imf组的周期-能量图')
得:
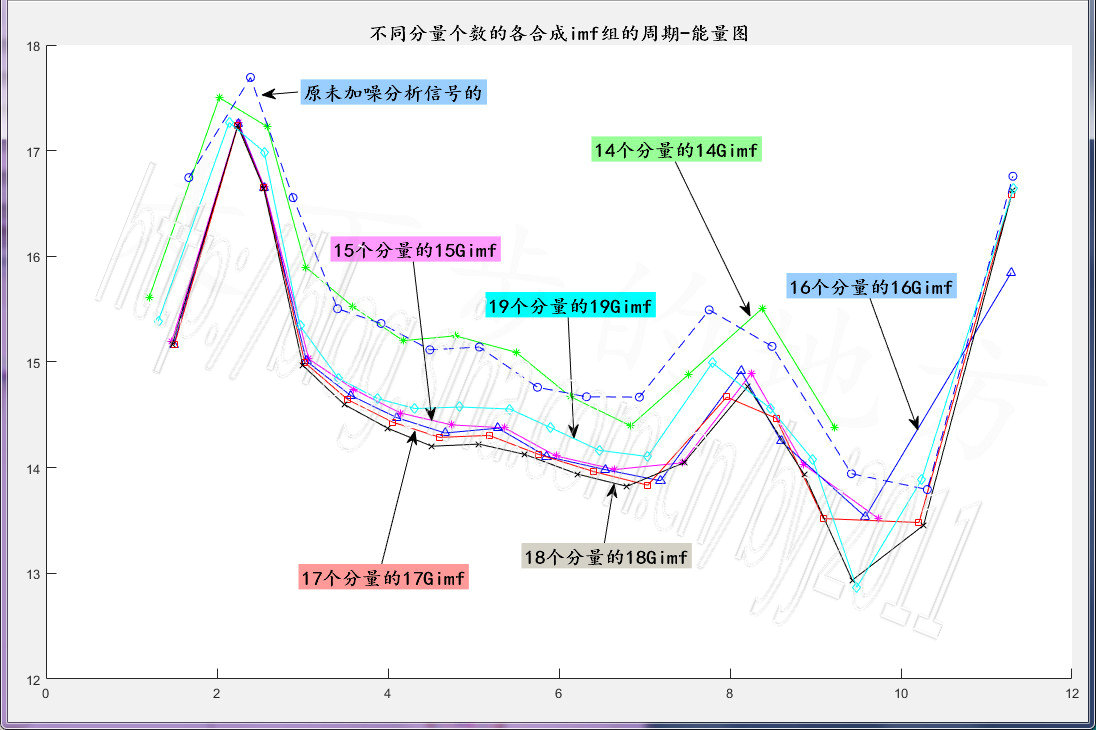
图71-2 原始信号imf0及各Gimf最大合imf各分量之周期-能量图
14Gimf周期-能量图与原分析信号imf0周期能量图极接近,可能跟14Gimf合成的组数10组太少有关。
此图仅作为资料保存。
各Gimf各分量周期:
zq1412=zq14/12;
zq14365=zq1412/365.2422;
zq1512=zq15/12;
zq15365=zq1512/365.2422;
zq1612=zq16/12;
zq16365=zq1612/365.2422;
zq012=zq0/12;
zq0365=zq012/365.2422;
zq1712=zq17/12;
zq17365=zq1712/365.2422;
zq1812=zq18/12;
zq18365=zq1812/365.2422;
zq1912=zq19/12;
zq19365=zq1912/365.2422;
zq14=[zq14,zq1412,zq14365];
zq15=[zq15,zq1512,zq15365];
zq16=[zq16,zq1612,zq16365];
zq0=[zq0,zq012,zq0365];
zq17=[zq17,zq1712,zq17365];
zq18=[zq18,zq1812,zq18365];
zq19=[zq19,zq1912,zq19365];

图71-3 14Gimf、15Gimf、16Gimf各分量平均周期

图71-4 原体温分析信号之imf各分量平均周期

图71-5 17Gimf、18Gimf、19Gimf各分量平均周期
上面7栏中,第1列为“时辰”,第2列为“天”,第3列为“年”。
可以看出,14Gimf、15Gimf的数据是不能用的,因为连18年(多)这个大能量长周期都没有。而这个长周期,无论在图形中还是在上上篇博文自相关函数分析中都是已经确定无疑的。
其余各周期数据,目前暂且只能放在这里,在日后其它方法分析周期时作为佐证资料。
各合16Gimf各正交指数(向量)之均值、标准差
mort=mean(ort);
sort=std(ort);
maort=mean(aort);
saort=std(aort);
maaort=aaort;
saaort=0;

图71-6 原体温信号imf0及各合16Gimf正交指数
ort0是原体温信号imf0的正交指数,ort是初次分解的16Gimf长度为2100的正交指数向量,
aort为十合16Gimf长度为210的正交指数向量,aaort为2100合16Gimf之正交指数。
mort0、mort、maort、maaort;sort0、sort、saort、saaort分别是上述4个正交指数(向量)
的均值与标准差。
与上篇博文数据比较,可以看出16Gimf正交指数较17Gimf正交指数略小,
意即前者分解质量较后者略优。
上面是16Gimf正交指数
下面把初次分解的14Gimf、15Gimf、16Gimf、17Gimf、18Gimf、19Gimf之正交指数都调出来放在一起,加以比较:
for i=1:10
ort14(i)=ST14_10(i).ort;
end
for i=1:781
ort15(i)=ST15_781(i).ort;
end
for i=1:1486
ort18(i)=ST18_1486(i).ort;
end
for i=1:21
ort19(i)=ST19_21(i).ort;
end
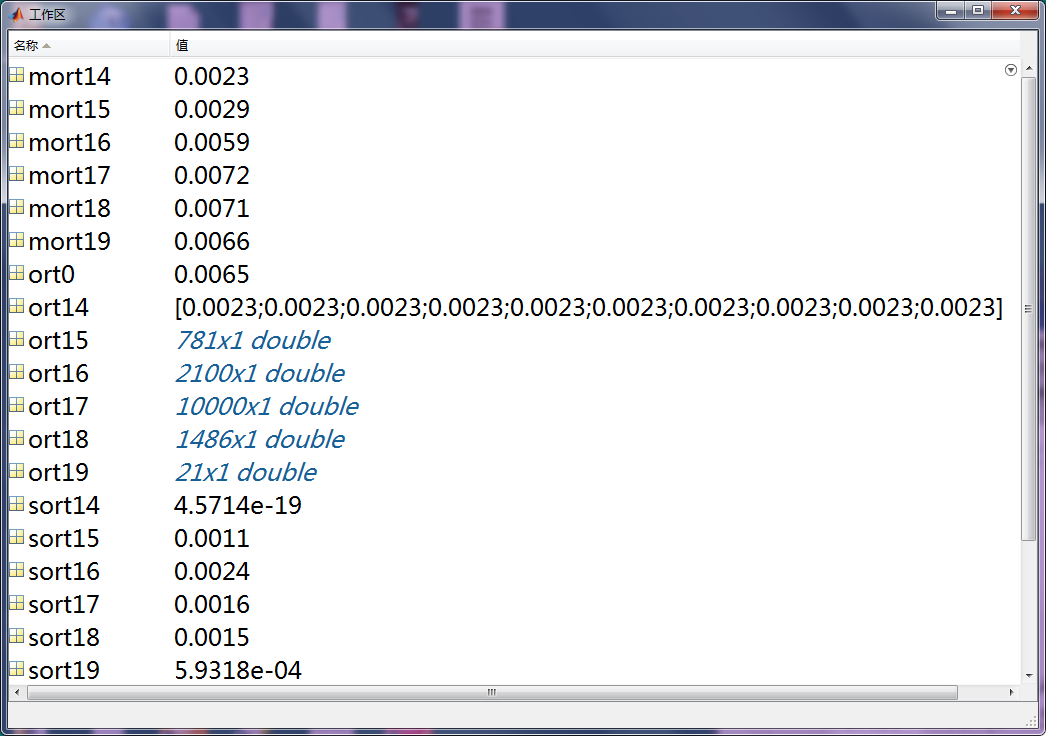
图71-7 各Gimf正交指数
上表中,ort0是原体温分析信号imf0之正交指数,ort14、ort15、ort16、ort17、ort18、ort19分别是
14Gimf、15Gimf、16Gimf、17Gimf、18Gimf、19Gimf之正交指数(向量)。
向量名前加“m”的是其均值,加“s”的是其标准差。
可以很容易看出,分解出组数最多的17Gimf,其正交指数最大,意即分解质量最差。
https://blog.sciencenet.cn/blog-825323-1226179.html
上一篇:70、体温信号总体经验模式分解(eemd)研究(一)
下一篇:72、续说《“双盲试验”的盲区》