博文
70、体温信号总体经验模式分解(eemd)研究(一)
|||
70、体温信号总体经验模式分解(eemd)研究(一)
我在博文《51、根据imf分量个数分组_我的eemd方法(一)》谈了eemd分组分解方法。现在继续研究eemd。
令输入
x=TW793312(:)';%体温分析信号,行向量。
nstd=0.1;
n=10000;
进行分解。
原分析信号x:imf0=emd(x),得到的imf0是一组16个分量(含残余项。下同)的imf,
但经过加噪处理的信号xr:
lx=length(x);
sd=std(x);
r=randn(1,lx);
ran=r*sd*nstd;
xr=x+ran;
经过试运行后,确认得到分量个数最多的分解,是17个分量的分解。
因此分解次数n=10000次是针对17个分量的分解而言。
由于n=10000太大,分做了10次运行,每次运行n=1000次,10次运行花了4天3夜。另外由于系统不稳、不熟、失误而丢失数据,总共花了将近10天(夜)才完成这项任务。
程序:
function [ST,ST3,ST2,ST1,ST_1,ST_2,ST_3]=imfstr(x,nstd,n);
lx=length(x);
sd=std(x);
dv=17;% dv=size(imf,1);分解所得imf个数
i=1;
ST=[];
ST3=[];
ST2=[];
ST1=[];
ST_1=[];
ST_2=[];
ST_3=[];
m3=1;
m2=1;
m1=1;
m_1=1;
m_2=1;
m_3=1;
while i<=n
r=randn(1,lx);
ran=r*sd*nstd;
xr=x+ran;
[imf o v]=emd(xr);
%分解所得imf个数等于原分析信号分解所得imf个数时
if size(imf,1)==dv;
ST(i).imf=imf;
ST(i).ort=o;
ST(i).ran=ran;
i=i+1;
%分解所得imf个数比原分析信号分解所得imf个数多出3个时
elseif size(imf,1)>=dv+3;
ST3(m3).imf=imf;
ST3(m3).ort=o;
ST3(m3).ran=ran;
m3=m3+1;
%分解所得imf个数比原分析信号分解所得imf个数多出2个时
elseif size(imf,1)==dv+2;
ST2(m2).imf=imf;
ST2(m2).ort=o;
ST2(m2).ran=ran;
m2=m2+1;
%分解所得imf个数比原分析信号分解所得imf个数多出1个时
elseif size(imf,1)==dv+1;
ST1(m1).imf=imf;
ST1(m1).ort=o;
ST1(m1).ran=ran;
m1=m1+1;
%分解所得imf个数比原分析信号分解所得imf个数少出1个时
elseif size(imf,1)==dv-1;
ST_1(m_1).imf=imf;
ST_1(m_1).ort=o;
ST_1(m_1).ran=ran;
m_1=m_1+1;
%分解所得imf个数比原分析信号分解所得imf个数少出2个时
elseif size(imf,1)==dv-2;
ST_2(m_2).imf=imf;
ST_2(m_2).ort=o;
ST_2(m_2).ran=ran;
m_2=m_2+1;
%分解所得imf个数比原分析信号分解所得imf个数少出3个时
elseif size(imf,1)<=dv-3;
ST_3(m_3).imf=imf;
ST_3(m_3).ort=o;
ST_3(m_3).ran=ran;
m_3=m_3+1;
end
end
end
为了叙述方便,以后我把16个分量的imf称作“16Gimf”,17个分量的imf称作“17Gimf”。。。余类推。
将16Gimf的数量记做“n16Gimf”,17Gimf的数量记做“n17Gimf”。。。余类推。
在n=10000次的目标下,最后得到的结果是:
n19Gimf=9;
n18Gimf=702;
n17Gimf=10000;
n16Gimf=6386;
n15Gimf=354;
n14Gimf=3;
下面只看10000组17Gimf。我把10组,100组、1000组、10000组 17Gimf 加和取均得到的17Gimf分别称为十合17Gimf、百合17Gimf、千合17Gimf、万合17Gimf。研究的目的有三个个:1,看imf各分量的“周期-能量”点在加和取均过程中的聚散性;2,看imf各分量的“异常极值点(大于0的极小值与小于0的极大值)”在加和取均过程中的位置聚散性与数量变化趋势。3,看各合之imf组的正交指数变化情况。
下面函数ALf=ALST(ST)中,输入 ST 是存有1000组17Gimf的结构变量,输出 ALf 是存有100组的十合17Gimf的结构变量:
function ALf=ALST(ST);
Lx=size(ST(1).imf,2);
for h=1:10
STh=ST((h-1)*100+1:(h-1)*100+100);
for i=1:10
BL(i).imf=zeros(17,Lx);
for j=1:10
k=(i-1)*10+j;
BL(i).imf=BL(i).imf+STh(k).imf;
end
AL(i).imf=BL(i).imf/10;
end
ALf((h-1)*10+1:(h-1)*10+10)=AL;
end
下面函数中,输入x是原体温分析信号,ALf是存有100组十合17Gimf的结构变量,
输出AL是存有100组十合17Gimf及其异常极值点、各分量周期-能量信息及各组正交指数的结构变量;
AAL 是存有10组百合17Gimf及其异常极值点、各分量周期-能量信息及各组正交指数的结构变量;
AAAL 是存有1组千合17Gimf及其异常极值点、各分量周期-能量信息及各组正交指数的结构变量;
ALp、AALp、AAALp分别是100组十合17Gimf、10组百合17Gimf、1组千合17Gimf的第JJ分量中异常极值点平均数
function [AL,ALp,AAL,AALp,AAAL,AAALp]=A123L(x,ALf);
x=x(:)';%行向量
Lx=length(x);% 95196;
zs=zeros(1,Lx);
figure(20);
W=1080;
H=720;
fg=figure(20);
set(fg,'position',[70,50,W,H]);
set(gca,'position',[0.035,0.06,0.95,0.88]);
figure(25);
W=1080;
H=720;
fg=figure(25);
set(fg,'position',[70,50,W,H]);
set(gca,'position',[0.035,0.06,0.95,0.88]);
figure(30);
W=1080;
H=720;
fg=figure(30);
set(fg,'position',[70,50,W,H]);
set(gca,'position',[0.035,0.06,0.95,0.88]);
%以下提取ALf各种参数,并作图
JJ=12;%选定十合17Gimf的第JJ个分量。
ALp=0;%十合17Gimf第JJ分量的异常极值点数。
for i=1:100
aimf=ALf(i).imf;
for j=1:16
imff=aimf(j,:);
[mn,mx,zr]=extr(imff);%输出分别为极小值、极大值、过零点
mnd=length(mn);%极小值个数
mxd=length(mx);%极大值个数
mnxd=mnd+mxd;%极值个数
AL(i).mnxd(j)=mnxd;%极值个数存档
mnz=find(imff(mn)>0);%大于零的极小值
mnzd=length(mnz);%大于零的极小值个数
mxf=find(imff(mx)<0);%小于零的极大值
mxfd=length(mxf);%小于零的极大值个数
AL(i).mnzc{j}=mn(mnz);%大于零的极小值位置存档
AL(i).mxfc{j}=mx(mxf);%小于零的极大值位置存档
mzfd=mnzd+mxfd;%异常极值总数
AL(i).mzfd(j)=mzfd;%异常极值总数存档
mdt=mzfd/mnxd;%异常极值占极值总数比例
AL(i).mdt(j)=mdt;%存档
z9=zr(end);%最后一个过零点位置
z1=zr(1);%第一个过零点位置
zl=length(zr);%过零点数量
zq=2*( z9-z1)/(zl-1);%imff周期
AL(i).zq(j)=zq;%周期存档
nl=imff*imff';%imff的能量。
AL(i).nl(j)=nl;%能量存档。
figure(20)
hold on
plot(log(zq),log(nl),'.g')%此imff的周期-能量点
figure(25)
hold on
plot(j,AL(i).mdt(j),'.g')%此imff的异、常极值点数比
end
ALp=ALp+AL(i).mzfd(JJ);%各组17Gimf的第JJ分量异常极值个数累计
mnz=AL(i).mnzc(JJ);%各组imf的第JJ分量大于零极小值调出
mnz=cell2mat(mnz);%转换
mxf=AL(i).mxfc(JJ);%各组imf的第JJ分量小于零极大值调出
mxf=cell2mat(mxf);%转换
AL(i).imf=ALf(i).imf;
imff=AL(i).imf(JJ,:);%imfJJ分量调出
figure(30)
hold on
plot(mnz,imff(mnz),'.g')%打印出100组十合17Gimf的第JJ分量大于零的极小值
hold on
plot(mxf,imff(mxf),'.g')%打印出100组十合17Gimf的第JJ分量小于零的极大值
hold on
plot(zs)
%下面计算该组aimf的正交指数
s = 0;
for j = 1:17
for k =1:17
if j~=k
fj=aimf(j,:);
fk=aimf(k,:);
fc=(fj*conj(fk)')/(x*x');
s = s + abs(fc);
end
end
end
AL(i).ort=s/2;
end
ALp=ALp/100;0组十合17Gimf第JJ分量的异常极值点数平均。
%以下将AL中的100组十合17Gimf累加平均,得到10组百合17Gimf,存于AAL
for i=1:10
AAL(i).imf=zeros(17,Lx);
for j=1:10
k=(i-1)*10+j;
AAL(i).imf=AAL(i).imf+AL(k).imf;组十合17Gimf累加
end
AAL(i).imf=AAL(i).imf/10;%平均,得到1组百合17Gimf,存于AAL。
end
% AAL存了10组百合17Gimf。
%以下提取AAL各种参数,并作图
AALp=0;
for i=1:10
aaimf=AAL(i).imf;
for j=1:16
imff=aaimf(j,:);
[mn,mx,zr]=extr(imff);
mnd=length(mn);%极小值个数
mxd=length(mx);%极大值个数
mnxd=mnd+mxd;
AAL(i).mnxd(j)=mnxd;%极值个数之和
mnz=find(imff(mn)>0);%大于零的极小值
mnzd=length(mnz);%大于零的极小值个数
mxf=find(imff(mx)<0);%小于零的极大值
mxfd=length(mxf);%小于零的极大值个数
AAL(i).mnzc{j}=mn(mnz);%大于零的极小值位置
AAL(i).mxfc{j}=mx(mxf);%小于零的极大值位置
mzfd=mnzd+mxfd;%异常极值总数
AAL(i).mzfd(j)=mzfd;%异常极值总数存档
mdt=mzfd/mnxd;%异常极值占极值总数比例
AAL(i).mdt(j)=mdt;
z9=zr(end);
z1=zr(1);
zl=length(zr);
zq=2*( z9-z1)/(zl-1);
AAL(i).zq(j)=zq;
nl=imff*imff';
AAL(i).nl(j)=nl;
figure(20)
hold on
plot(log(zq),log(nl),'*b')
figure(25)
hold on
plot(j,mdt,'*b')
end
AALp=AALp+AAL(i).mzfd(JJ);% 10组百合17Gimf的第12分量异常极值个数累加。
mnz=AAL(i).mnzc(JJ);%各组imf的第12分量大于零极小值调出
mnz=cell2mat(mnz);%转换
mxf=AAL(i).mxfc(JJ);%各组imf的第12分量小于零极大值调出
mxf=cell2mat(mxf);%转换
imff=AAL(i).imf(JJ,:); % 17Gimf第12分量调出
figure(30)
hold on
plot(mnz,imff(mnz),'*b')%打出10组百合17Gimf的第12分量大于零的极小值
hold on
plot(mxf,imff(mxf),'*b')%打出10组百合17Gimf的第12分量小于零的极大值
plot(zs)
%下面计算该组aaimf的正交指数
s = 0;
for j = 1:17
for k =1:17
if j~=k
fj=aaimf(j,:);
fk=aaimf(k,:);
fc=(fj*conj(fk)')/(x*x');
s = s + abs(fc);
end
end
end
AAL(i).ort=s/2;
end
AALp=AALp/10;%得到10组百合17Gimf的第12分量的异常极值点数平均值
%以下将AAL中的10组百合17Gimf累加平均,得到1组千合17Gimf,存于AAAL
AAAL.imf=zeros(17,Lx);
for i=1:10
AAAL.imf=AAAL.imf+AAL(i).imf;
end
AAAL.imf=AAAL.imf/10;
%以下提取AAAL各种参数,并作图
aaaimf=AAAL.imf;
for j=1:16
imff=aaaimf(j,:);
[mn,mx,zr]=extr(imff);
mnd=length(mn);%极小值个数
mxd=length(mx);%极大值个数
mnxd=mnd+mxd;
AAAL.mnxd(j)=mnxd;%极值个数之和
mnz=find(imff(mn)>0);%大于零的极小值
mnzd=length(mnz);%大于零的极小值个数
mxf=find(imff(mx)<0);%小于零的极大值
mxfd=length(mxf);%小于零的极大值个数
AAAL.mnzc{j}=mn(mnz);%大于零的极小值位置
AAAL.mxfc{j}=mx(mxf);%小于零的极大值位置
mzfd=mnzd+mxfd;%异常极值总数
AAAL.mzfd(j)=mzfd;%异常极值总数存档
mdt=mzfd/mnxd;%异常极值占极值总数比例
AAAL.mdt(j)=mdt;
z9=zr(end);
z1=zr(1);
zl=length(zr);
zq=2*( z9-z1)/(zl-1);%imff周期
AAAL.zq(j)=zq;%周期存档
nl=imff*imff';%imff的能量。
AAAL.nl(j)=nl;%能量存档。
figure(20)
hold on
plot(log(zq),log(nl),'^k')
figure(25)
hold on
plot(j,mdt,'^k')
end
imff=aaaimf(JJ,:);
[mn,mx,zr]=extr(imff);
mnz=find(imff(mn)>0);
mxf=find(imff(mx)<0);
AAALp=length(mnz)+length(mxf);
figure(30)
hold on
plot(mn(mnz),imff(mn(mnz)),'^k')
plot(mx(mxf),imff(mx(mxf)),'^k')
plot(zs)
%下面计算该组aaaimf的正交指数
s = 0;
for j = 1:17
for k =1:17
if j~=k
fj=aaaimf(j,:);
fk=aaaimf(k,:);
fc=(fj*conj(fk)')/(x*x');
s = s + abs(fc);
end
end
end
AAAL.ort=s/2;
end
上面所得到的AAAL是存有1组千合17Gimf的结构变量。它由存有1000组原初17Gimf的结构变量ST所得。
最初分解了10000组17Gimf,因此有10个这样的ST变量,记为ST01、ST02、ST03、ST04、ST05、ST06、ST07、ST08、ST09、ST10。分别作同样运算,得到10个这样的AAAL结构变量,分别记为AAAL01、AAAL02、
AAAL03、AAAL04、AAAL05、AAAL06、AAAL07、AAAL08、AAAL09、AAAL10。
令AAAL=[AAAL01,AAAL02,AAAL03,AAAL04,AAAL05,AAAL06,AAAL07,AAAL08,AAAL09,AAAL10];
以下函数输入此AAAL,输出AAAAL含1组万合17Gimf,及其各分量之异常极值点信息。
AAAALp是其指定的第JJ分量的异常极值点个数。x是原体温分析信号。
function [AAAAL,AAAALp]=A34L(x,AAAL);
x=x(:)';
Lx=length(x);
z=zeros(1,Lx);
%以下将10组AAAL的千合17Gimf累加平均,得到1组万合17Gimf,
%存于AAAAL中。
AAAAL.imf=zeros(17,Lx);
for i=1:10
AAAAL.imf=AAAAL.imf+AAAL(i).imf;
end
AAAAL.imf=AAAAL.imf/10;
%以下提取AAAAL各种参数,并作图
aaaaimf=AAAAL.imf;
for j=1:16
imff=aaaaimf(j,:);
[mn,mx,zr]=extr(imff);
mnd=length(mn);%极小值个数
mxd=length(mx);%极大值个数
mnxd=mnd+mxd;
AAAAL.mnxd(j)=mnxd;%极值个数之和
mnz=find(imff(mn)>0);%大于零的极小值
mnzd=length(mnz);%大于零的极小值个数
mxf=find(imff(mx)<0);%小于零的极大值
mxfd=length(mxf);%小于零的极大值个数
AAAAL.mnzc{j}=mn(mnz);%大于零的极小值位置
AAAAL.mxfc{j}=mx(mxf);%小于零的极大值位置
mzfd=mnzd+mxfd;%异常极值总数
AAAAL.mzfd(j)=mzfd;%异常极值总数存档
mdt=mzfd/mnxd;%异常极值占极值总数比例
AAAAL.mdt(j)=mdt;
z9=zr(end);
z1=zr(1);
zl=length(zr);
zq=2*( z9-z1)/(zl-1);%imff周期
AAAAL.zq(j)=zq;%周期存档
nl=imff*imff';%imff的能量。
AAAAL.nl(j)=nl;%能量存档。
figure(20)
hold on
plot(log(zq),log(nl),'or')%^b
plot(log(zq),log(nl),'pr')
figure(25)
hold on
plot(j,mdt,'or')% log()*b
plot(j,mdt,'pr')
end
imff=AAAAL.imf(12,:);
[mn,mx,zr]=extr(imff);
mnz=find(imff(mn)>0);
mxf=find(imff(mx)<0);
AAAALp=length(mnz)+length(mxf);
figure(30)
hold on
plot(mn(mnz),imff(mn(mnz)),'or')%^b
plot(mn(mnz),imff(mn(mnz)),'pr')
plot(mx(mxf),imff(mx(mxf)),'or')%^b
plot(mx(mxf),imff(mx(mxf)),'pr')
plot(z)
%下面计算该组aaaaimf的正交指数
s = 0;
for j = 1:17
for k =1:17
if j~=k
fj=aaaaimf(j,:);
fk=aaaaimf(k,:);
fc=(fj*conj(fk)')/(x*x');
s = s + abs(fc);
end
end
end
AAAAL.ort=s/2;
end
如前所述,我一共分解了10000组17Gimf,分成了10部分,每部分1000组17Gimf,分别存在结构变量ST01、ST02......ST10中。对每个ST施行上述运算,每起运算可以得到一组长度分别为100、10、1的十、百、千合的AL、AAL、AAAL17Gimf,每组17Gimf对应1个正交指数。
提取每部分ST中的ort数据:
ST=ST01;%ST02、ST03。。。
for i=1:1000
ort(i)=ST(i).ort;
end
得到10段长度各为1000的ort(ort01、ort02。。。)
提取AL17Gimf中的ort:
AL=AL01;%AL02、AL03。。。
for i=1:100
aort(i)=AL(i).ort;
end
得到10段长度各为100的aort。
提取AAL17Gimf中的ort:
AAL=AAL01; % AAL02、AAL03。。。
for i=1:10
aaort(i)=AAL(i).ort;
end
得到10段长度各为10的aaort。
提取AAAL17Gimf中的ort:
aaaort=AAAL17.ort;
得到10个aaaort。
将上面10段(个)ort、aort、aaort、aaaort合并,得到长度分别为10000、1000、100、10的ort、
aort、aaort、aaaort.
再将AAAAL17Gimf中的ort提取:
aaaaort=AAAAL.ort;
计算各正交指数向量的方差、标准差:
mort=mean(ort);
sort=std(ort);
maort=mean(aort);
saort=std(aort);
maaort=mean(aaort);
saaort=std(aort);
maaaort=mean(aaaort);
saaaort=std(aaaort);
maaaaort=aaaaort;
saaaaort=0;
现在可以贴图了:

图70-1 十百千万合17Gimf各分量的周期-能量图
可以看出:1、随着合成组数的增加,各分量的周期-能量点逐步向1点聚集。
2,有3个(组)分量的能量特别大:第2(3)分量、第12(13)分量与第16分量。
它们与我上一篇博文中的“图69-4 自相关函数emd分解各分量周期-能量关系图”
的特征是一致的,只是imf分量的个数、序数不一样而已。
具体的周期数据,待下一篇与14、15、16、18、19Gimf一起分析。
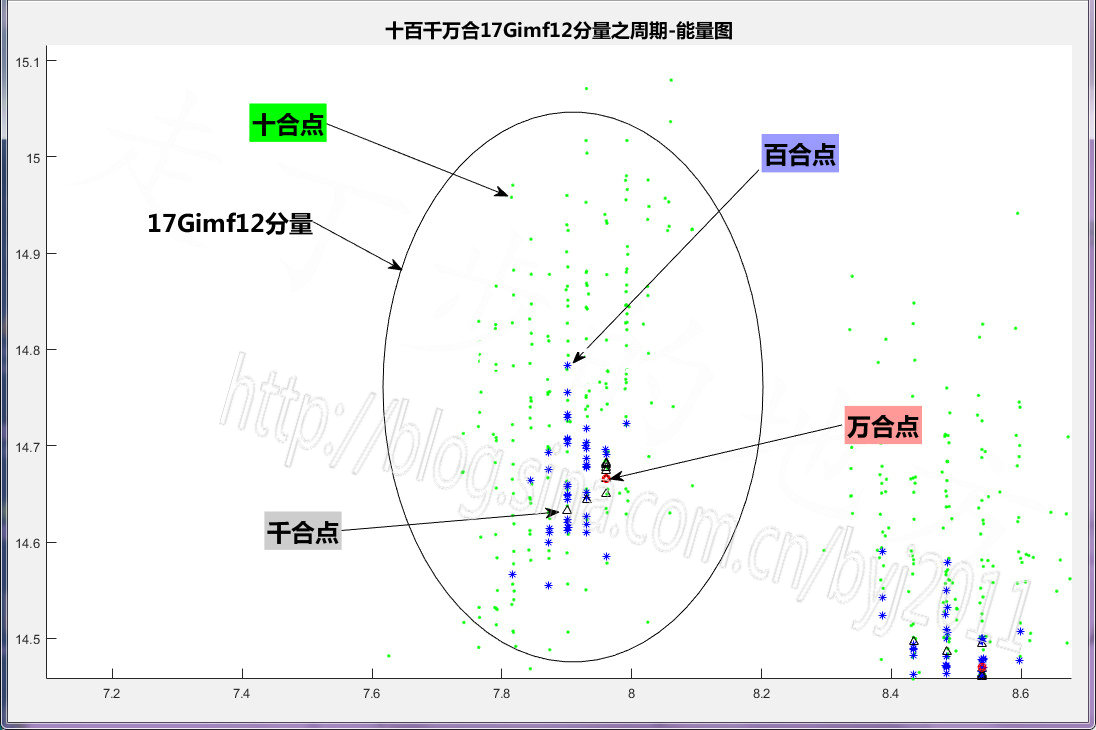
图70-2 上图局部放大图
可以看出,周期-能量点主要在纵轴能量方向聚集,而在横轴周期方向是向右
侧某一极限值收敛,而且是“有级、跳跃性”的。

图70-3 十百千万合17Gimf各分量异常极值点占总极值点数比例
变化比较复杂。1,在短周高频分量中,占比受合成次数影响较小,而在长周低频分量中,
受合成次数影响很大。合成次数越少占比越大,合成次数越多占比越小。
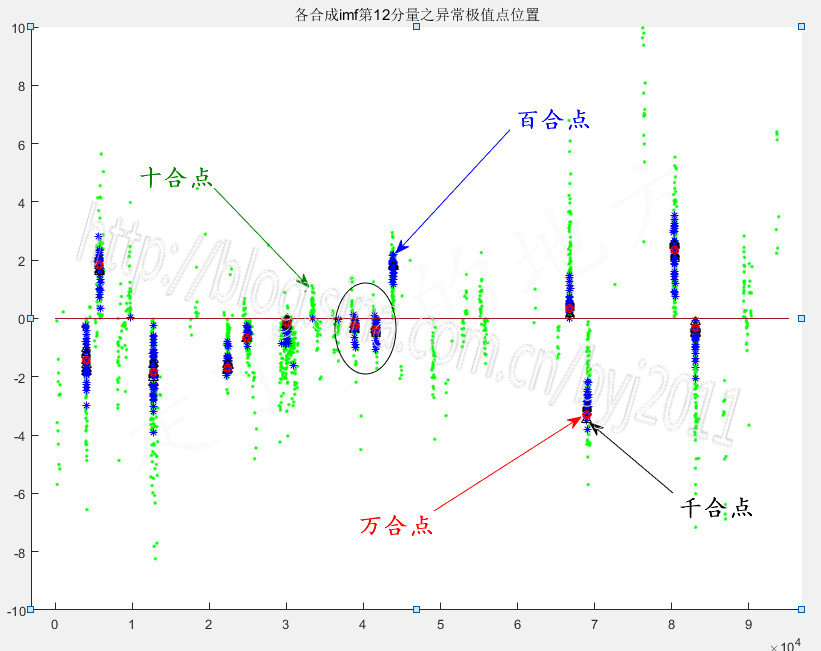
图70-4 十百千万合17Gimf第12分量的异常极值点数量与位置
特点分析:1、随着合成次数的增加,异常极值点会向某一些位置聚集
2、在幅值方向上的收敛是连续的,在时间上的收敛是分级(离散)的。
3、在时间点上,聚集的位置最后会固定在几处,而最初的一些位置会被完全“抛弃”。
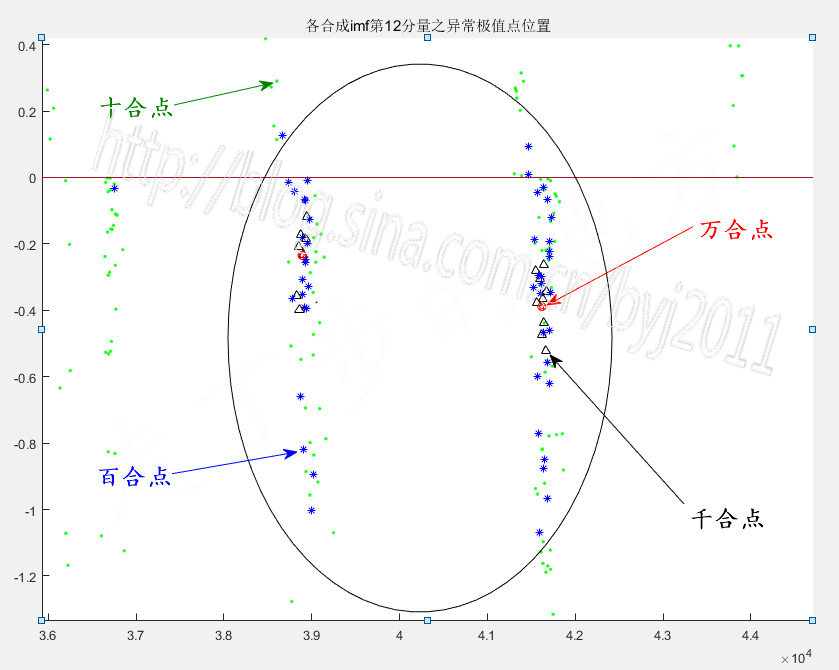
图70-5 上图放大
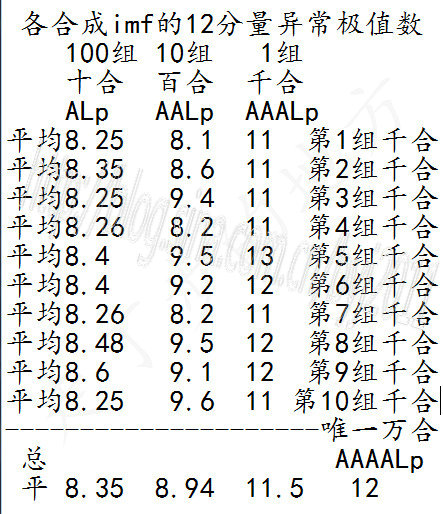
图70-6 十百千万合17Gimf第12分量的异常极值点平均数
从此表可以确定,增加imf的总体合成组数,其各分量中异常极值点数量不但不会减少,而且还会增加。因此通过增加合成组数的方法,是不可能得到严格的imf(无异常极值点)的。
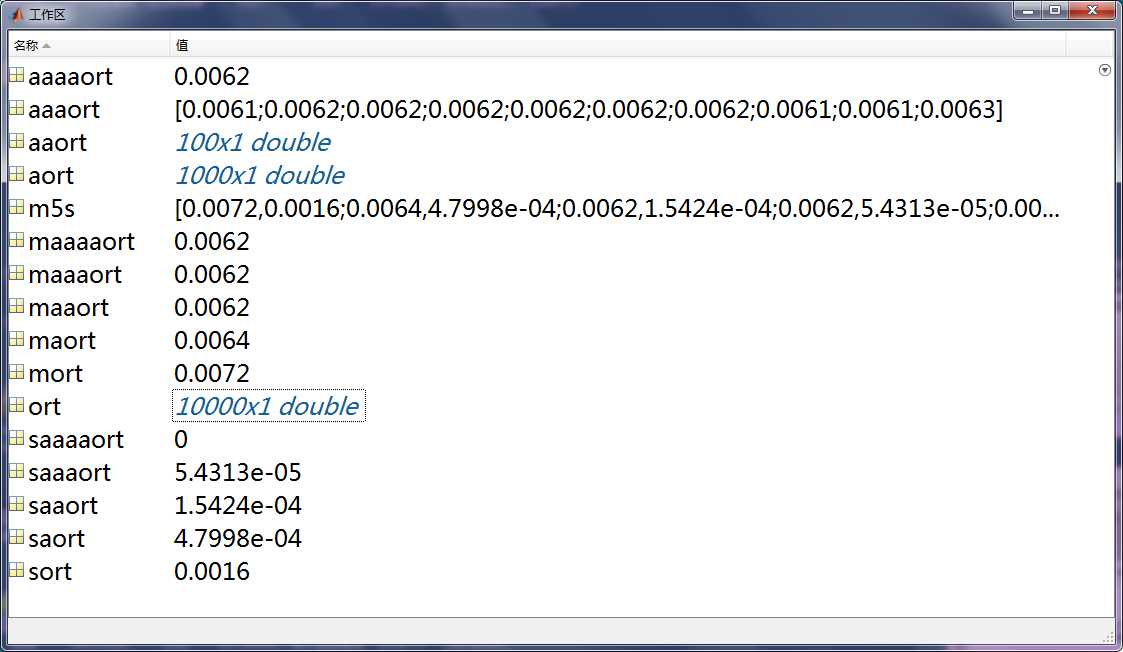
图70-7 各合17Gimf之正交指数向量及其均值、标准差。
ort、aort、aaort、aaaort、aaaaort、分别是初次分解、十、百、千、万合17Gimf正交指数向量。
mort、maort、maaort、maaaort、maaaaort、分别是上述正交指数的均值;
sort、saort、saaort、saaaort、saaaaort、分别是上述正交指数的标准差。
m5s是将上面10个变量合在一起,以方便截图查看更精确的数据。下图即该截图。
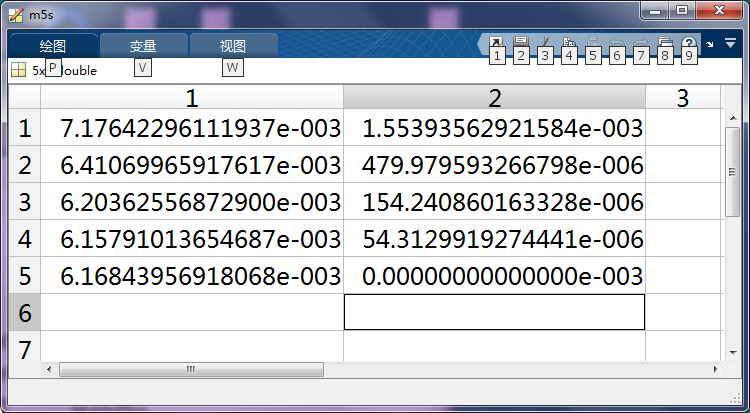
图70-8 各合17Gimf正交指数的均值、标准差(长数据)
第1、2、3、4、5行分别为万组初次分解、千组十合、百组百合、十组千合、一组万合17Gim正交指数的
均值与标准差。
第1列为均值,第2列为标准差
可以看出从第1~第4行的正交指数均值都是递减的。第5行略有增加,但由于数据太少,从第4行右侧的标准差来看,完全可以断定属于随机误差。因此可以得出结论:随着参加叠加合成的imf组数的增加,合成所得imf组的正交指数是递减的,且远小于0.
最后,来看看得到的唯一的一组万合17Gimf各分量图形
imf=AAAAL.imf;
lx=95196;%size(imf,2);
zs=zeros(1,lx);
W=1080;
H=720;
m=6;
n=3;
k=17;
fg=figure(1);
set(fg,'position',[80,50,W,H]);
for i=1:m
for j=1:n
p=j+(i-1)*n;
if p<=k
s(p)=subplot(m,n,p);%
set(s(p),'position',[0.025+(j-1)/n,0.005+(m-0.95*(0.999^i)*i)/m,0.92/n,0.72/m]);
x=imf(p,:);
plot(x)
hold on
plot(zs,'k--')
mx=max(x);
mn=min(x);
xn=mx-mn;
axis([fix(-0.1*lx) fix(1.1*lx) mn-0.1*xn mx+0.1*xn])
end
end
end
title('万合17Gimf各分量图')
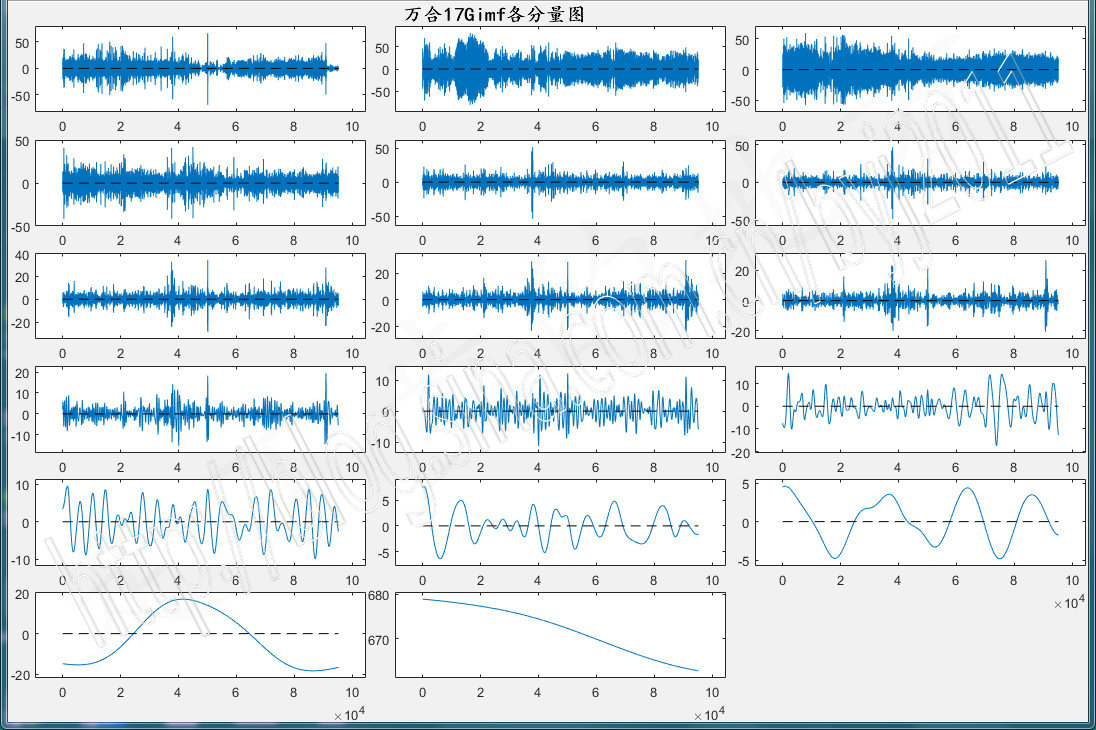
图70-9 万合17Gimf各分量
看看各分量周期:
zq=AAL.zq';
zq12=zq/12;
zq365=zq12/365.2422;
ZQ=[zq,zq12,zq365];
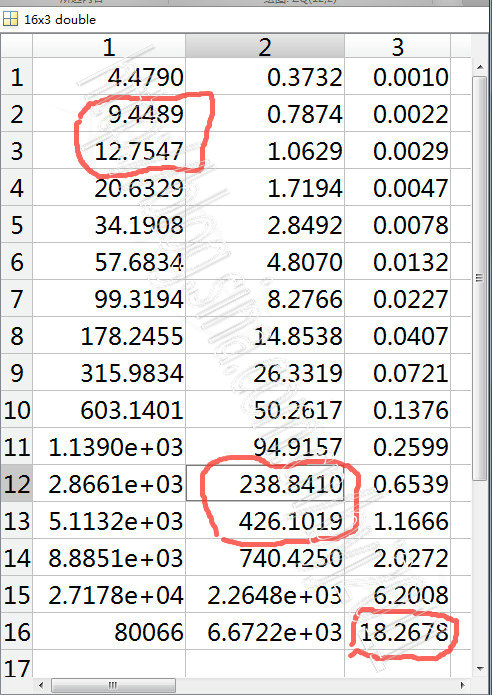
图70-10 万合17Gimf各分量周期
图中红圈标示的是图70-1中3组5个高能量分量的周期。
可以看出,第1组两个周期,正好位于“时干周期10时辰”与“时支周期12时辰”两侧,
第2组两个周期,正好位于“月干周期10个月约300天”与“月支周期1年约365天”两侧,
虽然具体数字还有差距,但我相信这绝不是偶然的。内在原因需要进一步探索。
此数据经过这样大规模imf总体合成,结果的随机性已经极低了,它更多反映的是信号系统(人体)
内在的固有结构特征。
最后看看第12分量及其异常极值点大图
imf=AAAAL.imf;
lx=95196;%size(imf,2);
zs=zeros(1,lx);
W=1080;
H=720;
imf12=imf(12,:);
fg=figure(2);
set(fg,'position',[80,50,W,H]);
set(gca,'position',[0.03,0.05,0.95,0.90]);
plot(imf12)
hold on
plot(zeros(1,95196))
mnzc12=cell2mat(AAAAL.mnzc(12));
mxfc12=cell2mat(AAAAL.mxfc(12));
plot(mnzc12,imf12(mnzc12),'or')
plot(mxfc12,imf12(mxfc12),'or')
title('万合17Gimf第12分量及其异常极值点图')
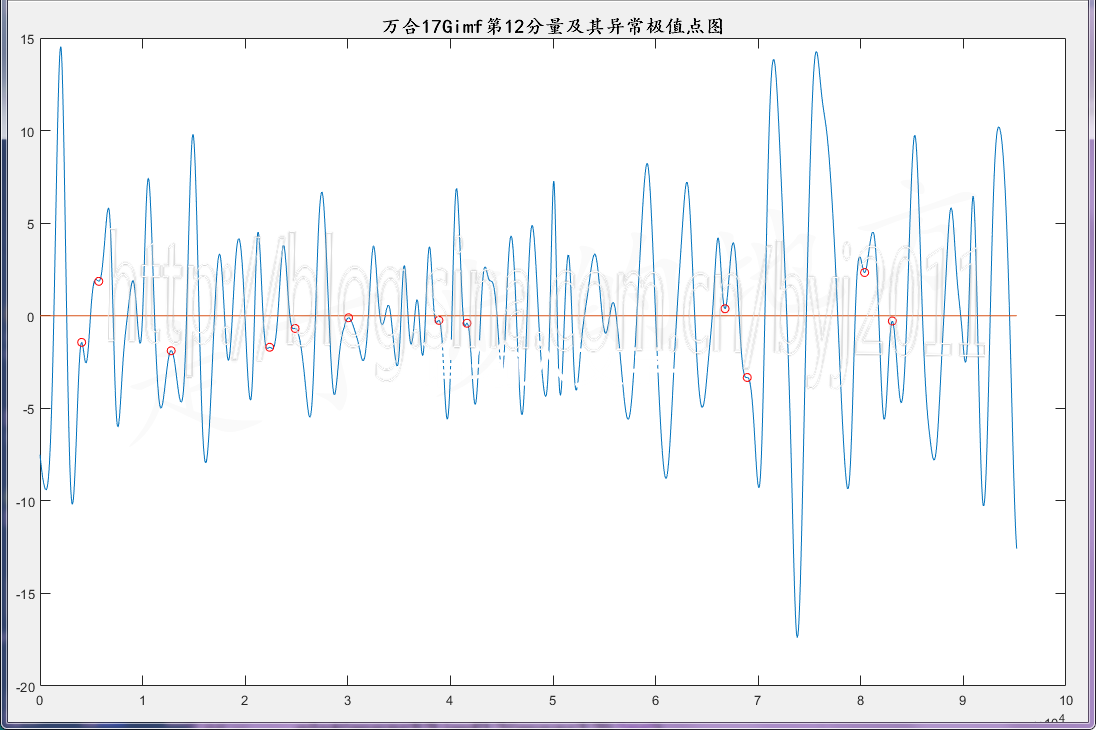
图70-11 万合17Gimf第12分量及其异常极值点图
经过10000次的总体合成,这些异常极值点的位置都已经具有很大的必然性了。它反映的是人体的一些固有特征。在物理系统中,异常极值点是表示系统输出在复平面上的反转。对人体来说,这种“反转”也是有生理学意义的。中医中本来就有呃逆、气逆、逆动、逆乱、逆症。。。等概念。此“异常极值点”说不定就与此有关。总之这些信息可以处理到此为止,只需留待以后作“模式识别”。
https://blog.sciencenet.cn/blog-825323-1226168.html
上一篇:69、长期精密体温数据自相关函数周期分析
下一篇:71、体温信号总体经验模式分解(eemd)研究(二)