博文
[请注意] “P对NP, P vs NP”问题与“无穷 infinity”无关
||
“人是社会关系的总和,人不能脱离社会而存在。”
汉语是联合国官方正式使用的 6 种同等有效语言之一。请不要歧视汉语!
Chinese is one of the six equally effective official languages of the United Nations.
Not to discriminate against Chinese, please!
[请注意] “P对NP, P vs NP”问题与“无穷 infinity”无关
核心:“P对NP”问题与“无穷”之间无任何关系
术语:
P对NP: P vs NP, P versus NP
确定型图灵机: DTM, deterministic Turing machine
非确定型图灵机: NTM, non-deterministic Turing machine
集合论: set theory
无穷: infinity
康托: Georg Cantor, Georg Ferdinand Ludwig Philipp Cantor
无穷公理: axiom of infinity
策梅洛-弗兰克尔集合论: ZFC, Zermelo–Fraenkel set theory with the axiom of choice
一、“P对NP”问题与“无穷”无关
“P对NP”的一个准确介绍,请看“P vs NP”, The Millennium Prize Problems, Clay Mathematics Institute。这里不再解释。
NTM 相当于 DTM 的幂集,都是有穷的。
请注意:
“P对NP”是有穷情况下的问题。该问题与“无穷”无关。
因此,在研究“P对NP”时,根本不用考虑“对无穷公理(The axiom of infinity)的任何反对意见”。
换言之,“P对NP”和“无穷”之间没有关系。真正的“风马牛不相及”。
“君处北海,寡人处南海,唯是风马牛不相及也。”完全不必“不虞君之涉吾地也,何故?”【您住在北方,我住在南方,双方相距遥远,即使马、牛奔驰,也不会跑到对方的境内。没想到您进入了我们的国土,这是什么缘故?】
https://so.gushiwen.cn/mingju/juv_0fcce49cf6e8.aspx
二、“P对NP“与 SCIENCE 期刊的两次 125问题
2.1 《科学》期刊 2005年第一次 125 问题
SCIENCE, VOLUME 309|ISSUE 5731|1 JUL 2005
https://www.science.org/toc/science/309/5731
其中第 19 个问题是:
What Are the Limits of Conventional Computing? 常规计算的极限是什么?
2.2 2021年上海交大携手《科学》杂志向全球发布125个科学问题
这是2005年以后,《科学》杂志第二次向全球发布的125个科学问题。
https://news.sjtu.edu.cn/mtjj/20210412/145693.html
与“P对NP”有关的问题有 4 个以上:
Information Science 信息科学
1. Is there an upper limit to computer processing speed? 1.计算机处理速度是否有上限?
Artificial Intelligence 人工智能
3. Is there a limit to human intelligence? 3.人类智力是否有极限?
7. Can quantum artificial intelligence imitate the human brain? 7.量子人工智能可以模仿人脑吗?
Physics 物理学
17. What is the optimum hardware for quantum computers? 17.量子计算机的最佳硬件是什么?

上面的例子,可以“通俗”地说明“P对NP”的价值了吧?
三、对“无穷公理的任何反对意见”,目前都是“非主流”
尽管康托“被”迫害成精神病,但是,由于道德楷模希尔伯特(David Hilbert)的维护,集合论却发展成为数学的基础:“ZFC公理集合论是万有理论,能够推导出经典数学的所有理论。”
https://www.zgbk.com/ecph/words?SiteID=1&ID=456822&Type=bkzyb&SubID=137849
希尔伯特用坚定的语言向他的同代人宣布:“没有任何人能将我们从康托尔所创造的伊甸园中驱赶出来。 Aus dem Paradies, das Cantor uns geschaffen, soll uns niemand vertreiben können. No one shall expel us from the Paradise that Cantor has created.”
对“无穷公理(The axiom of infinity)的任何反对意见”,目前都是“非主流”。这是个数学常识。
您有权怀疑或反对“无穷公理(the axiom of infinity)”,但一定要清楚:这是“非主流”的。
实际上,为了发展“集合论”,怕是将来不得不重新思考“无穷”了:我一直觉得“康托无穷级数第一序列”有点不对劲。这也使我只使用“康托无穷级数第二序列”。
自然有人反对“对角线方法”,反对“实无穷”,反对……
您有权利反对!但和“P对NP”无关。
您有权利反对!大概率将来我也“怀疑”。
但是,
请不要忘记:我们是地球人!“三体人”怎么看待“无穷”,目前和我们地球人没有直接的关系。
2023-06-28 后补,进一步请看:
[1] 2023-06-28,[补充扼要说明] “P对NP, P vs NP”问题的“1+3”种证明与无穷
https://blog.sciencenet.cn/blog-107667-1393320.html
参考资料:
[1] P vs NP, The Millennium Prize Problems, Clay Mathematics Institute
https://www.claymath.org/millennium/p-vs-np/
[2] 2022-01-20,时间复杂性类/time complexity class/许道云,中国大百科全书,第三版网络版[DB/OL]
https://www.zgbk.com/ecph/words?SiteID=1&ID=208077&Type=bkzyb
[3] 2023-04-11,康托尔,G./Georg (Ferdinand Ludwig Philipp) Cantor/王宪钧 撰、程钊 修订,中国大百科全书,第三版网络版[DB/OL]
https://www.zgbk.com/ecph/words?SiteID=1&ID=182825&Type=bkzyb&SubID=61733
[4] 2022-07-13,策梅洛-弗兰克尔集合论/Zermelo-Fraenkel set theory/杜国平,中国大百科全书,第三版网络版[DB/OL]
https://www.zgbk.com/ecph/words?SiteID=1&ID=229361&Type=bkzyb&SubID=104156
[5] 2023-01-18,数学基础/foundations of mathematics/何浩平
https://www.zgbk.com/ecph/words?SiteID=1&ID=456822&Type=bkzyb&SubID=137849
同时发展出的公理集合论成为了事实上的数学基础。
20世纪初数学基础研究的结果,是数学家们在实践中接受了公理化的集合论作为经典数学的基础。
[6] 2022-01-20,冯•诺伊曼-博内斯-哥德尔公理系统/von Neumann-Bernays-Gödel axiomatic system/杜国平
https://www.zgbk.com/ecph/words?SiteID=1&ID=229203&Type=bkzyb
公理化集合论系统之一,简称NGB系统,又称GB系统。
NGB系统是一致的,当且仅当ZF系统是一致的,即两者具有相对一致性。就仅表达集合的命题而言,NGB系统和ZF系统是等价的。
[7] 2022-04-21,十九世纪数学/mathematics in 19th century/袁向东
https://www.zgbk.com/ecph/words?SiteID=1&ID=182506&Type=bkzyb&SubID=61733
[8] Complexity theory. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Complexity_theory
[9] NP. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/NP
[10] Infinity. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Infinity
[11] Axiomatic set theory. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Axiomatic_set_theory
[12] ZFC. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/ZFC
[13] Infinity, axiom of. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Infinity,_axiom_of
[14] SCIENCE, 2005-01-07, Special Issue 125th Anniversary, 01 JULY 2005, VOL 309, ISSUE 5731
https://science.sciencemag.org/content/309/5731
[15] SCIENCE, 2021-04-11, 125 questions: Exploration and discovery, In honor of Shanghai Jiao Tong University’s 125th Anniversary
https://www.sciencemag.org/collections/125-questions-exploration-and-discovery
[16] 《科学通报》, 季铮锋, 夏盟佶. What are the limits of conventional computing? 计算的极限,2016 年第 61 卷第 4-5 期:404 ~ 408.
https://www.sciengine.com/CSB/doi/10.1360/N972015-01363
[17] 柳渝,2023-05-21,关于康托尔理论的争议
https://blog.sciencenet.cn/blog-2322490-1388860.html
相关链接:
[1] 2021-05-15,《科学》杂志的两个 125个科学问题(2005,2021)
https://blog.sciencenet.cn/blog-107667-1286678.html
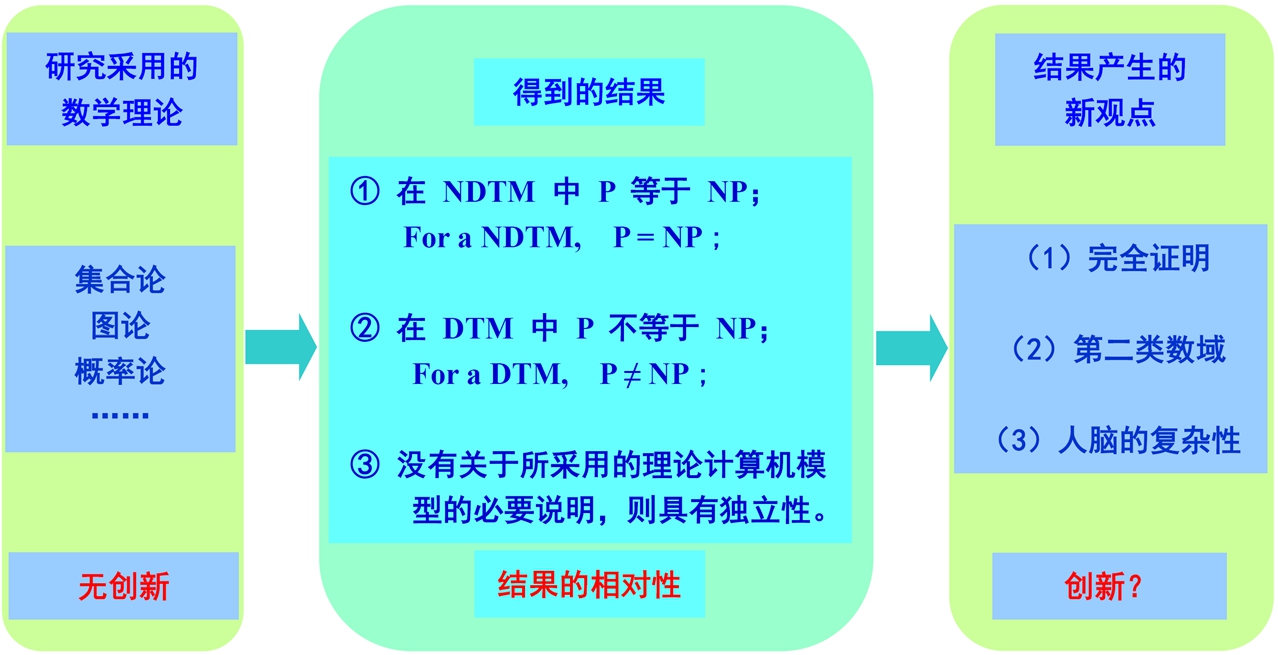
[2] 2022-06-10,[请教] P对NP(二):结果的相对性与“1+3”种证明
https://blog.sciencenet.cn/blog-107667-1342404.html
[3] 2023-02-11,[随笔] “P对NP, P vs NP, P versus NP” Problem 问题:问题与求解方法
https://blog.sciencenet.cn/blog-107667-1375792.html
[4] 2023-01-17,[说明] 我对“P对NP”的所有研究,使用的都是现有的主流数学理论
https://blog.sciencenet.cn/blog-107667-1372343.html
[5] 2015-05-22,The kernel of "P vs NP Problem": Axiom of power set!
https://blog.sciencenet.cn/blog-107667-892400.html
[6] 2012-03-23,[请教] P对NP:请***教授等专家指教(一)
https://blog.sciencenet.cn/blog-107667-550859.html
[7] 2011-12-05,TTU论文《A non-canonical example to support that P is not equal to NP》已经刊出
https://blog.sciencenet.cn/blog-107667-515297.html
[8] 2011-09-15,A FULL PROOF to the P versus NP problem
https://blog.sciencenet.cn/blog-107667-486692.html
[9] 2011-09-06,My report and papers on "the P versus NP problem" (P vs NP)
https://blog.sciencenet.cn/blog-107667-483639.html
[10] 2020-08-17,小忆“第2类数学(智能数学)”的提出
https://blog.sciencenet.cn/blog-107667-1246726.html
[11] 2010-08-27,11年前的记忆:人脑复杂性的估计及其哲学意义
https://blog.sciencenet.cn/blog-107667-356704.html
[12] 2023-01-13,[???] 为什么在“四色问题 The four colour theorem”上长期不肯吱声?
https://blog.sciencenet.cn/blog-107667-1371830.html
感谢您的指教!
感谢您指正以上任何错误!
感谢您提供更多的相关资料!
https://blog.sciencenet.cn/blog-107667-1393194.html
上一篇:[笔记,思考] 反射太阳能给地球降温
下一篇:[补充扼要说明] “P对NP, P vs NP”问题的“1+3”种证明与无穷