博文
量子化学与奥本海默
||
量子化学与奥本海默
近来,由于电影《奥本海默》的上映,各网站和科普公众号上关于奥本海默的文章颇多,其议题大多在与原子弹有关的政治或人性。我没有看此电影,对于奥本海默的了解也不多,只是想说一说与奥本海默有关的一门学科——量子化学。
在化学的各个分支学科中,量子化学是比较晚起的。所谓量子化学,就是用量子力学的理论和方法去解决化学问题。建立于20世纪20年代的量子力学,给与化学这门比较古老的科学以革命性的变化。
原子和分子理论是化学的最基础的理论,但是,在量子力学建立以前,人们一直弄不清楚原子到底是怎样能够组合成为分子的。有人相信存在一种“化学力”,以使原子组合成分子,但是什么是化学力,谁也说不清楚。
量子力学建立以后,人们知道了,由于原子由原子核和电子组成,它们都是微观粒子,它们的运动应当服从量子力学的运动规律,所以,原子-分子体系的运动状态应当是薛定谔方程的解。
定态薛定谔方程是一个与体系的坐标有关的二阶微分方程。对于化学体系,不失一般性,反应可由如下方程式所示:
A + B = C + D
其中A、B、C、D是四个由原子组成的广义的分子,四个分子所含有的原子个数不全为零。其中A+B为反应物体系,C+D为产物体系。
由于原子由原子核和电子组成,而化学反应前后原子核和电子的个数不会发生变化。所以,这个化学反应,从微观的角度看,只是反应体系中的那些原子核和电子的位置即坐标发生了变化。当两个原子核相距足够远的距离,我们就认为它们不在同一个分子里了。
我们研究的体系实际上就是A+B体系中所含有的原子核和电子。
为了叙述的方便,我们随便举一个例子。假定A分子为甲烷CH4,有5个原子核和16个电子,B分子为氯原子,有1个原子核和17个电子,这样,体系共有6个原子核(4个氢核、1个碳核、1个氯核)和33个电子所组成。为了确定一个粒子的空间位置,需要有3个坐标变量(往往称有三个自由度)。6个核,需要18个坐标变量;33个电子,需要99个坐标变量。
这样,我们要解的薛定谔方程中共有6个核的坐标变量,33个电子的坐标变量。在薛定谔方程每一个粒子的动能算符部分,还与粒子的质量有关,而这6个核的质量分成三种,33个电子的质量倒都是一样的。在方程的势能部分,有核与电子的吸引作用,电子与电子之间的排斥作用以及核与核之间的排斥作用。我们看到,即使是这样简单的一个化学反应,体系的薛定谔方程就非常复杂。
解偏微分方程的主要方法是分离变量法。这个方法是把含有多个变量的偏微分方程化为多个只含单变量的常微分方程。但是这里的势能函数中原子核坐标与电子坐标交织在一起,使得这个方程不能严格地分离变量。
1927年,德国哥廷根大学23岁的罗伯特·奥本海默(Robert Oppenheimer)和他的导师马克斯·玻恩(Max Born)发表了一篇论文,提出一个解决此问题的方法。
这个方法的基本出发点是,由于核的质量远远大于电子的质量,而质量的差别,表示着粒子运动速度变化的难易程度。
我们从事体育活动比如打篮球,都知道小个子队员一般都比大个子灵活。因为质量小意味着运动的惯性小,容易转身而改变运动速度(包括大小和方向)。原子核的质量比电子的质量要大几千到几万倍甚至更多。即使是最轻的核,氢原子的核,只有一个质子,其质量是电子质量的1836倍。其他原子都比氢原子核质量大得多,例如碳原子核,则通常是氢原子核的12倍(即电子质量的2.2万倍),氧核是氢核的16倍(电子的接近3万倍),银核则接近氢的108倍(电子的近20万倍)等等。
如此巨大的质量差距,使得电子的移动速度的变化会较原子核快很多。这一速度变化差异的结果是,对于原子核位置的微小变化,电子都能迅速调整以适应这种变化。因此可以近似地认为电子是在静止原子核的势场中运动。也就是说,人们可以先把各原子核固定在某一个位置(称为核构型),在这核构型下,求解关于电子运动的薛定谔方程,得到该构型下的电子波函数。
由此,可以实现原子核坐标与电子坐标的近似变量分离,将求解整个体系的波函数的复杂过程分解为求解电子波函数和求解原子核波函数两个相对简单的过程。
这个方法,被称为玻恩-奥本海默近似。当然,要具体地了解这个近似方法的数学表示,必须去看专门的教科书。
为了较为清楚地说明这个过程,我们看一个最简单的例子,氢分子的解离反应H2→H+H
对于氢分子体系,有两个氢原子,这样体系中有两个核和两个电子。这里,确定核构型的变量只有一个,就是两个核之间的距离。
先插进来说一个问题,我们上面说过一个粒子应当有3个坐标即3个自由度,两个粒子应当有6个自由度。怎么这里只剩下一个变量了呢?因为我们在这里只研究氢分子本身的性质,分子在空间平动(有3个自由度)不影响其性质;这个分子的两个核在一直线上,分子在空间转动(对线性分子有2个自由度)也基本上不影响其性质。所以影响其性质的自由度只剩下一个,就是两个核之间的距离。
现在固定两个核之间的距离为某一个值,即固定其核构型。在这个核构型下,求解电子的定态薛定谔方程,可得到在这个构型下的各个可能的电子能量值(称为能量本征值)和与其对应的电子运动波函数。
换一个核间距,再求解这个构型下的各个能量本征值和与其对应电子运动波函数。
当把核间距从小到大所有的核构型下的薛定谔方程都求解出来之后,就得到了体系电子能量与核间距之间的函数关系。由于只有一个变量,函数值在二维的平面直角坐标系下表现为一根曲线。考虑到两个核之间是有排斥能的,把这个核-核排斥能与电子能量加在一起,就可以得到如下的曲线(横轴为核间距,纵轴为能量)。下图只画出来能量最低的两条曲线。
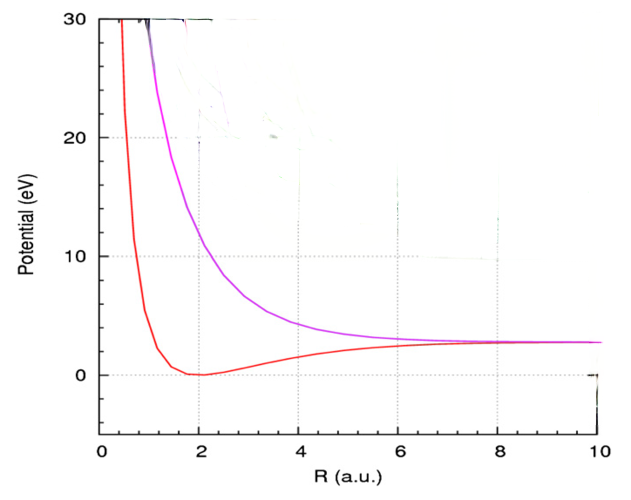
其中最低的那个状态称为基态,较高的是第一激发态。
由于曲线的值在求解核坐标的薛定谔方程时,是该方程的势能函数,所以该曲线被称为氢分子的势能曲线。
由图可见,氢分子基态势能曲线有一个最小值。使得体系处在能量最小值处的核间距就是氢分子基态的平衡核间距,也就是通常所说的氢分子的键长,处在这个核间距的氢分子具有最低的能量,也就是最稳定。从这个图上,我们能够很清晰地看出由基态氢分子解离为两个氢原子即化学反应H2→H+H过程中的能量变化。
从最简单的氢分子体系,到一般的分子体系,其求解方程的过程与上面所说的氢分子体系完全相似,不过就是变量的个数即空间的维数增加了而已。
假定体系总共有N个原子,这个体系的核构型,将有3N-6个核坐标变量(每一个核3个坐标,共计3N个坐标,再去除表示体系质心平动的3个坐标和体系转动的3个坐标)。解出每一种构型下电子运动的薛定谔方程,可以得到它们的能量本征值和电子运动波函数。把全部构型的能量本征值都求出,分别再加上核-核排斥能,就得到了核运动的薛定谔方程中的势能。由于共有3N-6个核坐标变量,势能可以表示为3N-5维空间的一个超曲面,被称为体系的势能面。
势能面上每一个对于所有的3N-6个坐标都取极小值的点,就对应于体系的一个平衡构型。对3N-7个坐标取极小值而对一个坐标取极大值的点,就对应于体系的一个过渡态。人们可以根据势能面上的这些特点,去判断化学反应的机理,即从反应物到产物所经由的可能路径。
求解电子运动的薛定谔方程,得到体系势能面上各特殊点的能量以确定体系的平衡构型和过渡态等信息,是用量子化学方法计算化学反应的重要内容。
至于从势能面出发求解核运动的薛定谔方程,则是另一个也非常艰巨的任务。它构成了量子力学分子反应动力学的重要内容。
这些过程一般都在玻恩-奥本海默近似的框架内进行。各种实验手段都证明,在体系的两个量子态相距得不很近的情况下,玻恩-奥本海默近似是一个非常好的近似方法,由此得到的理论计算值与实验值有很好的符合。
由于量子化学和分子反应动力学的理论研究和计算一般都在玻恩-奥本海默近似下进行,所以,这方面的书籍往往一开始就会介绍玻恩-奥本海默近似。
奥本海默在23岁时就能够对学科发展作出这样重要的贡献,是非常了不起的。他可以说是生逢其时,20世纪初的三十年正好是物理学科发生重大变革的年代,许多年轻的科学家在这个年代展示了他们的才华,成就了他们的不朽功绩。奥本海默也正好在这场大变革的中心学习和工作。他的导师又是为量子力学的建立作出卓越贡献的大物理学家玻恩。这真是所谓时势造英雄。当然,最根本的还是奥本海默自己的努力。
https://blog.sciencenet.cn/blog-612874-1402431.html
上一篇:说“人生最大的投资是你的孩子”
下一篇:什么是学术意见?
全部作者的精选博文
- • 杂说蔬菜(2)白菜
- • 杂说蔬菜(1)序
- • 杂说几个与里有关的字(2)
- • 杂说几个与里有关的字(1)
- • 杂说“里”
- • 灶与炉
全部作者的其他最新博文
- • 杂说蔬菜(2)白菜
- • 杂说蔬菜(1)序
- • 杂说几个与里有关的字(2)
- • 杂说几个与里有关的字(1)
- • 杂说“里”
- • 康铃康铃马来哉