博文
湍流最初产生的位置
|
本文是一篇科普文章,本文目的是为了向读者展示,通过预测湍流最初产生的位置来说明,自纳维-斯托克斯方程建立200年以来,在所有的关于湍流转捩、湍流产生以及完全发展的湍流维持的理论中,只有能量梯度理论是唯一正确的理论。纳维-斯托克斯方程是描述湍流的正确方程,奇点是层流转捩到湍流的唯一途径。
(一)湍流研究一般分为两个研究方向
(1)研究一个光滑的层流是怎样变为湍流的。100多年来,人们认为湍流是层流失稳引起的,所以这个研究方向被命名为:流动稳定性和湍流转捩。
(2)研究完全发展的湍流的特性及维持机理。包括湍流结构、能谱标度律、能量传递过程、阻力特性、统计规律,等。
流动失稳与湍流转捩不是一回事,过去,在国内外的教科书中都是混淆不清,没有叙述清楚。对于湍流研究的初学者必须注意到这个问题。湍流转捩:意思是流动从层流流动变成了湍流流动。流动失稳:意思是一种流动失去了稳定性,发生了状态的改变,从一种流动状态变成了另一种流动状态。作者认为,一个光滑的层流流动,在流动失稳后,可能变为湍流,也可能变为另一种层流,并不是层流失稳一定会变为湍流。教科书和文献中对海森堡1924和林家翘1944的研究工作都没有交代清楚,他们得到的平面Poiseuille 层流流动(线性)失稳,失稳后是另一种层流,并不是湍流。海森堡1924和林家翘1944预测的平面Poiseuille流动线性失稳的结果是基本正确的。而文献中说的林家翘先生(1944)的工作预测了湍流的产生是错误的,这个问题是以前人们对湍流的认识程度局限性所造成的。但是,在21世纪的今天,人们已经清楚认识到线性失稳不能导致湍流,所以应该纠正过来。不能人云亦云,继续写到教科书中去。
在湍流转捩的研究中,不仅要(a)预测湍流转捩的临界条件,(b)给出湍流转捩的物理学概念,(c)还要给出湍流产生的最初位置。对于湍流转捩,以前的各种理论研究都是仅仅集中在临界条件上,即预测临界雷诺数。就说临界雷诺数吧,没有哪一个理论预测能够与实验一致,包括线性稳定性理论、非线性稳定性理论、弱非线性稳定性理论、二次失稳理论、瞬态增长理论,等。湍流转捩并不是方程特征值为正的问题。混沌理论只是一种想法和模糊的定性解释,而且也没有解释清楚,更不能预测湍流临界雷诺数。
对于湍流转捩的物理学概念,即湍流转捩是怎么发生的,以前的理论都没有给出确切并且合乎实际的解释,原因是其机理都不知道。而对于湍流产生的最初位置,很少有人探讨过,而这恰恰是非常重要的,尤其对湍流控制。所有上面这些三个目标要求,只有能量梯度理论都做到了,也都成功了【1】。因此,能量梯度理论是一个颠覆性的理论。
(二)湍流最初产生的位置的理论预测
从雷诺在1883年在曼彻斯特做的圆管流动实验,确认了流动有层流、转捩流和湍流以来,已经过去了140年。通过100多年来的研究,人们已经逐渐认识到,湍流产生最初先从一个局部位置开始,例如边界层流动中是层流中先有湍流斑的出现,然后湍流斑增大及增多,最后发展为完全发展的湍流。湍流斑只是一个表面现象,深层次的物理机理必须通过Navier-Stokes方程来揭示【2,3】。层流转捩为湍流这个现象,其原理与固体力学中是类似的,比如就像一座桥梁,遭到破坏时,首先是先从某一个局部位置开始破坏,此处是安全系数最小的位置。此处有可能是产生了裂纹、材料缺陷,或者疲劳,等等。流体力学中,而对于湍流产生是此位置出现了奇点【1-3】。
在湍流研究领域,预测湍流最初产生的位置至关重要,比如工程应用中的湍流预防(或延迟)和控制。由于100多年来,湍流产生的机理不知道,所以就没有任何理论或方法可以预测这样的流动中最危险的位置。
窦华书教授提出了能量梯度理论【1-10】,用来研究湍流产生和湍流转捩。据此得到,湍流产生的必要和充分条件是流场中出现Navier-Stokes方程的奇点。那么就可以根据奇点的出现,来精确预测湍流最初产生的位置,从而对湍流进行控制。据此,对各种流动得到的湍流最初产生的位置,如图1中红色标记所示。(a)plane Poiseuille flow; (b) pipe Poiseuille flow; (c) plane Couette flow; (d) boundary layer flow; (e) circular jet; (f) wake behind circular cylinder; (g) mixing layer; (h) Taylor-Couette flow.
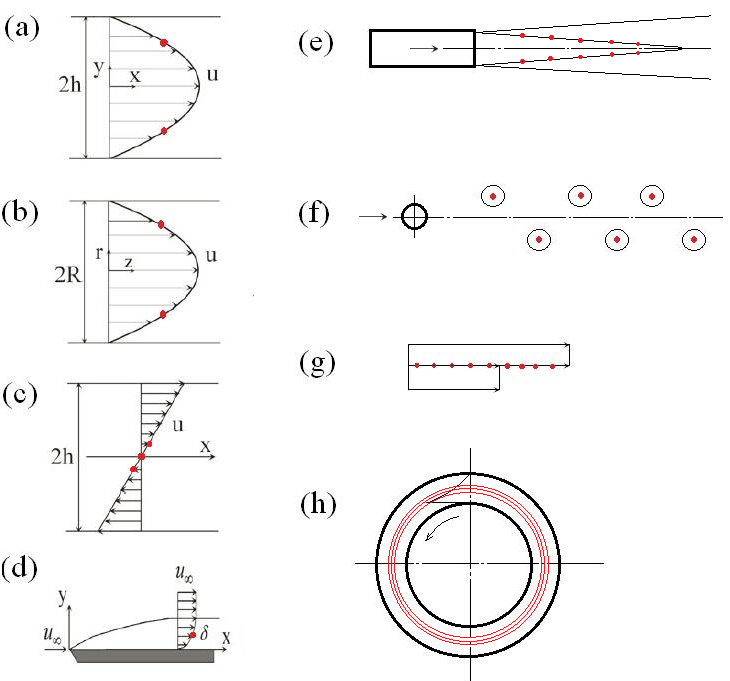
图1 能量梯度理论预测的湍流最初产生的位置 (红色标记所示)【1】。理论预测与实验结果完全一致。此图是能量梯度理论完全正确的最有力的证据之一。
对这些流动,预测的湍流产生的位置与实验数据以及DNS计算结果获得了完好的一致(图1)。没有发现任何反例。这是自纳维-斯托克斯方程建立,200年以来,第一次有人从理论上精确地预测了湍流最初产生的位置,这也是唯一的一个预测湍流产生位置的理论。在此之前,在国际国内,没有任何人、没有任何理论、或者任何方法,可以用来精确预测湍流产生的位置。对于实验和计算中展示的湍流最初产生的位置,一直没有引起湍流研究学者的足够注意,文献中也没有人给出合理的解释。
对湍流最初产生的位置,理论上有了这样的预测,我们就可以对湍流发生进行精准地控制。在固体力学里,对最危险位置可以增加加强筋,或者替换为高强度的材料。同理,在流体力学里,找到了湍流最初转捩的位置,我们就可以采用各种稳定性方法,对湍流产生进行干涉和控制。只要能延迟奇点产生,就能够延迟湍流产生。比如,降低速度亏损,以延迟奇点发生。
需要指出,一个层流最初失稳的位置,与后面湍流最先产生的位置,在有些情况下,并不一定是同一个位置。根据能量梯度理论,层流最初失稳的位置,是能量梯度函数K为最大值的位置。湍流最先产生的位置,一定是奇点产生的位置。
(三)压力驱动流动和剪切驱动流动中湍流产生的位置非常不同
对于壁面流动中的压力驱动流动,实验发现,流道的中心线上的湍流强度几乎为零,如pipe Poiseuille flow和plane Poiseuille flow(图1a,b), 以及弯曲管道内的Dean flow。而对于壁面流动中的剪切驱动流动,实验发现,流道的中心线上的湍流强度非常大,几乎与壁面附近的最大值是同一数量级,而且流道中心线位置是湍流最初产生的位置,如plane Couette flow和两个旋转同轴圆柱间的Taylor-Couette flow(图1c,h),以及图2所示。这种压力驱动流动和剪切驱动流动之间的现象的差别,是窦华书的能量梯度理论所精确预测到的,而没有任何其他湍流或流动稳定性方面的理论可以进行预测或者解释。图2所示的流道中心处的湍流转捩现象,在1997年就已经在实验和计算中发现了,可是20多年来,没有人给出合理解释。
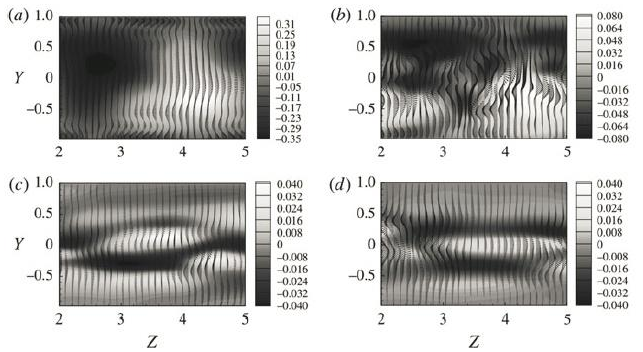
图2 平面Couette流动流道中心线(Y=0)附近湍流首先产生(Cherubini and De Palma 2015)。With the time increase, the flow evolves from (a) to (b), (c), and (d) in transitional flow.
压力驱动流动和剪切驱动流动中湍流产生的位置的巨大差异,来自于能量输入的不同。因为湍流的产生和维持,实际上是一个能量过程(输入、传递、消耗),只有考虑能量及做功变化的理论,才能真正描述湍流,这就是能量梯度理论得以成功的根本原因【1】。然而,其他的描述湍流的理论,都没有考虑这些因素。
平面Couette流动也是壁面流动,根据前面讨论,由于流道中心产生了高水平大尺度的湍流结构,很明显,用壁面湍流模型来预测平面Couette流动是不符合实际情况的。这就是为什么k-epsilon湍流模型来预测平面Couette流动失败的原因,k-epsilon湍流模型没有考虑壁面区以外的湍流结构。
因此,能量梯度理论预测及实验及数值模拟结果已经确认,压力驱动流动中湍流最初产生的位置,在两侧的中心线和壁面之间的位置。剪切驱动流动中湍流最初产生的位置,在流道中心线附近。
对于平面Couette流动和Taylor-Couette流动,湍流最先在流道中心产生,而不是在壁面附近,这是许多人都没有想到的,也无法解释。可是,这是事实【1】。绝大多数做流体力学研究的人,大多数做湍流研究的人,读到这里,各位许多人也是第一次听说吧?这不怪大家,毕竟湍流研究太难了!作者最初也没有想到,这是经过作者和他的合作者以及他指导的研究生做的DNS以及LES计算、实验观察和能量梯度理论分析预测,得到的真实且互相一致的结果 。精确的公式推导和基本原理,请见专著【1】的第4,5,6和9章。
最后指出,用能量梯度理论来研究湍流,不像教科书和文献中那样分为壁面湍流和自由湍流(说什么壁面湍流的机理是什么,自由流湍流的机理是什么),这里不分壁面湍流和自由湍流,因为它们的机理是相同的,是唯一的,都是Navier-Stokes方程的奇点导致的(奇点引起湍流猝发,上抛和下掠),是根据Navier-Stokes方程精确推导出来的,推导过程没有任何近似。壁面湍流和自由湍流的流动结构,如果进行高精度的精细的数值计算和数据分析,发现也是完全相同的,即发卡涡类似的结构【1】,壁面并不能对湍流结构改变起多大影响,毕竟壁面不是湍流产生与否的关键内在因素。换一个角度思考,如果像有些文献里讲的那样壁面是湍流产生的关键因素,那么自由流动里就不应该有湍流了,但事实不是如此。作者首次指出,壁面湍流和自由湍流的机理是相同的,湍流产生机理是唯一的,是Navier-Stokes方程的奇点所控制的 【1】。这已经得到实验和计算结果的验证。
事实胜于雄辩。一个新的理论正确与否,一是要基于第一性原理,二是要以事实为依据;只有与所有情况下的实验数据相一致的理论,才有可能是可靠的理论。做科研,就要有创新,就要有突破,就要敢于挑战和破解百年难题!
参考文献
1. Dou, H.-S., Origin of Turbulence-Energy Gradient Theory, 2022, Springer.
https://link.springer.com/book/10.1007/978-981-19-0087-7 (全书下载地址).
2. Dou, H.-S., Singularity of Navier-Stokes equations leading to turbulence, Adv. Appl. Math. Mech., 13(3), 2021, 527-553. https://doi.org/10.4208/aamm.OA-2020-0063 (AAMM); 或者
https://arxiv.org/abs/1805.12053v10 (Arxiv) (通过物理学推导出奇点)
3. Dou, H.-S., No existence and smoothness of solution of the Navier-Stokes equation, Entropy, 2022, 24, 339.
https://doi.org/10.3390/e24030339 (通过数学推导出奇点)
4.窦华书教授在纳维-斯托克斯方程问题上取得新进展,浙江理工大学官网新闻, 2021。
https://news.zstu.edu.cn/info/1033/41169.htm (此学校网页白天能打开,晚上打不开)
或者 https://mp.weixin.qq.com/s/8letL1Z5XiFf-6Lw4GLe5Q 或者
https://mp.weixin.qq.com/s/mnkwE67OPbGwHccqrePRrQ
5. 窦华书,一个力学公理的建立揭开了湍流的秘密, https://blog.sciencenet.cn/blog-3057857-1383011.html
6. 窦华书,千禧年大奖难题之一纳维-斯托克斯方程的解的存在性与光滑性的证明, 科学网博文,2022年5月。
https://blog.sciencenet.cn/home.php?mod=space&uid=3057857&do=blog&id=1337452
7. 窦华书,我是怎样创立能量梯度理论的? https://mp.weixin.qq.com/s/tujupDNxbClLCFXGBKJVIA
8. 窦华书:湍流及流动稳定性的公理、推论和定理, https://blog.sciencenet.cn/blog-3057857-1372119.html
9. 窦华书教授成功破解了百年湍流难题[转载], https://blog.sciencenet.cn/blog-3057857-1364433.html
10. 世界物理学百年难题——“湍流”之谜已被破解,文镁科技,2023年9月。
https://mp.weixin.qq.com/s/zx4Zi59i01arqwhtHrMSng
https://blog.sciencenet.cn/blog-3057857-1420133.html
上一篇:湍流是波
下一篇:研究湍流后来改行的世界著名科学家