博文
逻辑学对于发现与预测的重要性 -- 兼论美国国家三院特设委员会的数字孪生基础研究需求报告  精选
精选
||
[敬请读者注意] 本人保留本文的全部著作权利。如果哪位读者使用本文所描述内容,请务必如实引用并明白注明本文出处。如果本人发现任何人擅自使用本文任何部分内容而不明白注明出处,恕本人在网上广泛公布侵权者姓名。敬请各位读者注意,谢谢!
逻辑学对于发现与预测的重要性 -- 兼论美国国家三院特设委员会的数字孪生基础研究需求报告
程京德
“逻辑学是一门研究论证与推理之正确性的基础性学问,其目的为建立和建全用于判断各种论证与推理之正确性的一般标准。” [1] “逻辑学是最最重要的学问,没有任何其它学问比逻辑学更重要,因为逻辑学是任何其它学问之基础。” [2] “俗话说,逻辑学是“讲道理”的学问,并且,逻辑学要讲的是“一般的道理”,要追究的是不依赖于具体事物、放之四海而皆准的“一般的准则”。逻辑学有着其它学问所不具备的应用广泛性,恰恰是因为其一般性。这是逻辑学作为一门学问最最本质的特征。” [2]
“发现”是找出或揭示前所未知事物的过程。对于任何发现,在发现过程结束之前,所发现的事物及其真实性都是未知的(否则就完全用不着发现了)。
推理是从给定前提得出新结论的唯一途径。 因为在发现过程中被发现的事物及其真实性在发现过程完成之前是未知的,所以,没有不需要求助于推理的发现过程,发现必须求助于推理。由于任何发现过程都没有完全明确的清晰目标,因此任何发现过程必须遵循的唯一规范标准就是从前提推理出正确的结论,亦即,任何正确的有效的发现必须基于正确的推理。
“预测”是基于特定知识提前猜出未来(所以也当然是前所未知)事件之发生的过程。对于任何预测,在预测过程结束之前,预测出的事件及其发生时间都是未知的。预测可以被认为是涉及时间或时序的发现。
推理是从给定前提下得出新结论的唯一途径。 因为在预测过程中被预测出的事件及其发生在预测过程完成之前是未知的,所以,没有不需要求助于推理的预测过程,预测必须求助于推理。由于任何预测过程都没有完全明确的清晰目标,因此任何预测过程必须遵循的唯一规范标准就是从前提推理出正确的结论,亦即,任何正确的有效的预测必须基于正确的推理。
既然发现与预测都要基于正确的推理,而逻辑学是为推理提供正确性标准的学问,所以,逻辑学对于发现与预测的重要性就当然是不言而喻的了。如果没有逻辑学提供推理正确性标准作为最最基本的规范标准,那么人类社会科学与技术发展中的许多发现与预测都是不可能的,人类社会的文化、科学、技术都不可能发展到今天这样的高度。
因为有各种各样的推理,所以也有为各种各样的推理提供正确性标准的各种各样的逻辑系统 [3-6]。从是否合理地为发现与预测提供了正确性标准的角度来说,强相关逻辑是最合理的逻辑系统 [7-10]。
联合国教科文组织(UNESCO)在1988年修订的科学技术领域推荐国际标准术语表 [11] 中,把逻辑学和数学列为第一层次的两大基础学科,并且把逻辑学(编号11)列为第一位,数学(编号12)列为第二位。其它五大基础学科,天文学和天体物理学(编号21)、物理学(编号22)、化学(编号23)、生命科学(编号24)、地球与空间科学(编号25),被列为第二层次。第三层次才是农业科学(编号31)、医学(编号32)、技术科学(编号33)。而计算机科学(编号1203)被列为数学之一分支,计算机技术(编号3304)被列为技术科学之一分支。
因此,必须指出的非常重要的一点是,逻辑学是数学之(哲学)基础,数学并不包含逻辑学在内。尽管经典数理逻辑通常被认为是数学中的一个基础学科分支,但是,整个逻辑学的范围与内容远比经典数理逻辑要丰富的多得多。
2023年底,美国国家科学院、工程院、医学院(NAS、NAE、NAM)的特设委员会发表了数字孪生基础研究需求报告(以下简称“报告”)[12]。“科学院、工程院和医学院任命的特设委员会确认在科学、医学、工程和社会应用中推进数字孪生的数学、统计和计算基础的需求和机会 (Academies of Sciences, Engineering, and Medicine - appointed ad hoc committee will identify needs and opportunities to advance the mathematical, statistical, and computational foundations of digital twins in applications across science, medicine, engineering, and society.)”
数字孪生的想法最早出现在 Gelernter 的书中,Grieves 在2002年将其概念化, Vickers 在2010年引入了“Digital Twin”这个词来表达它 [13-15]。
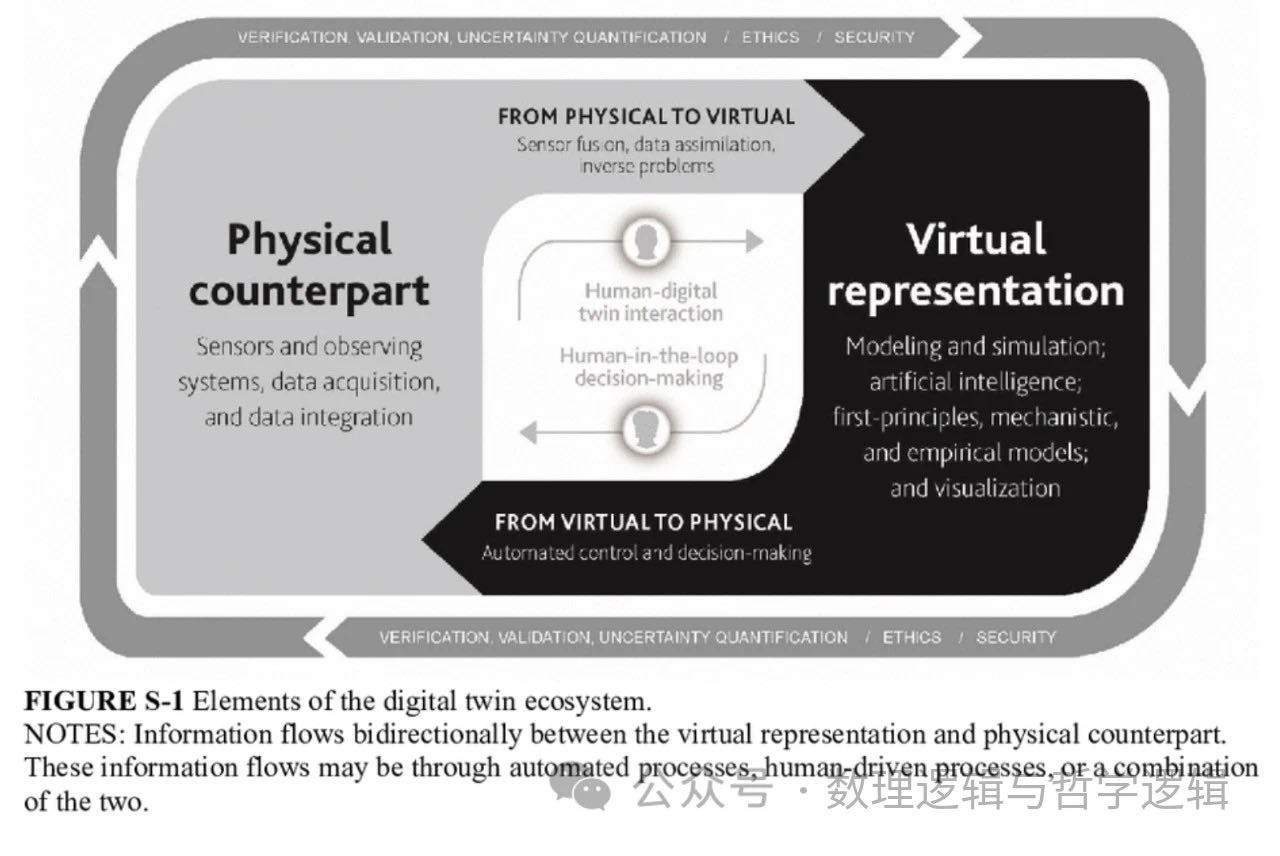
“数字孪生是一组虚拟信息结构,它模拟自然、工程或社会系统(或系统的系统)的结构、上下文和行为,通过使用物理孪生的数据动态地进行更新,具有预测能力,并为实现价值的决策提供信息。虚拟方和物理方之间的双向交互是数字孪生的核心。(A digital twin is a set of virtual information constructs that mimics the structure, context, and behavior of a natural, engineered, or social system (or system-of-systems), is dynamically updated with data from its physical twin, has a predictive capability, and informs decisions that realize value. The bidirectional interaction between the virtual and the physical is central to the digital twin.)” [12]
笔者认为,数字孪生,无论作为一种方法论还是作为一种具体技术,其最大的魅力/潜力就在于通过利用高速计算技术对在数字空间中的数字孪生系统的发现与预测,快速地反馈到现实空间中的目标物理系统而对目标物理系统之行为做出及时的甚至超前的调控。所以,左右数字孪生之将来的,应该是其发现与预测能力。
然而,尽管报告声称要阐明在几个领域推进数字孪生的关键性基础研究需求以及机遇,并且在报告中许多处强调了预测能力,但是该报告通篇没有提到过作为发现与预测之不可或缺基础的逻辑学,似乎发现和预测不需要关键性基础研究。因为该报告是个指引性纲领性的重要文献,所以笔者不得不说,对发现与预测之逻辑基础研究需求的忽视是该报告的一个重大缺陷。
蛇足一句。以预测作为最基本功能的超前计算系统(Computing Anticipatory Systems),其逻辑基础一直是一个基础研究问题 [16-19]。
参考文献
[1] 程京德,“逻辑学是什么”,微信公众号“数理逻辑与哲学逻辑”,2023年1月25日。
[2] 程京德,“逻辑学之重要性(及对其在中国被轻视之原因初探)”,微信公众号“数理逻辑与哲学逻辑”,2023年1月27日。
[3] 程京德,“为什么在逻辑学中存在有如此众多的不同逻辑系统?”,微信公众号“数理逻辑与哲学逻辑”,2023年1月28日。
[4] 程京德,“条件句:逻辑学中的最核心概念及最大难题”,微信公众号“数理逻辑与哲学逻辑”,2023年1月29日。
[5] 程京德,“形式理论:将形式逻辑系统应用于具体对象领域的逻辑基础”,微信公众号“数理逻辑与哲学逻辑”,2023年1月30日。
[6] 程京德,“形式逻辑系统中逻辑归结关系的形式化定义方法”,微信公众号“数理逻辑与哲学逻辑”,2023年2月1日。
[7] 程京德,“推理与证明之不同”,微信公众号“数理逻辑与哲学逻辑”,2023年5月7日。
[8] 程京德,“强相关逻辑及其应用(上)、(中)、(下)”,微信公众号“数理逻辑与哲学逻辑”,2023年6月18日、2023年8月8日、2023年8月12日。
[9] 程京德,“现代逻辑之未来 – 从相关逻辑到量子逻辑(纲要)”,微信公众号“数理逻辑与哲学逻辑”,2023年7月25日。
[10] 程京德,“实现人工通用智能的关键必由之路 -- 基于强相关逻辑的形式理论自动定理发现”,微信公众号“数理逻辑与哲学逻辑”,2023年10月19日。
[11] UNESCO, “Proposed International Standard Nomenclature for Fields of Science and Technology,” UNESCO/NS/ROU/257 rev.1, 1988.
[12] Academies of Sciences, Engineering, and Medicine,“Foundational Research Gaps and Future Directions for Digital Twins (2023),” Decmember 2023.
[13] D. H. Gelernter, “Mirror Worlds: or the Day Software Puts the Universe in a Shoebox — How It Will Happen and What It Will Mean,” Oxford University Press, 1991.
[14] M. Grieves, “Virtually Intelligent Product Systems: Digital and Physical Twins,” in S. Flumerfelt, et al. (Eds), “Complex Systems Engineering: Theory and Practice,” pp. 175-200, American Institute of Aeronautics and Astronautics, 2019.
[15] M. Grieves and J. Vickers, “Digital Twin: Mitigating Unpredictable, Undesirable Emergent Behavior in Complex Systems,” in F.-J. Kahlen, S. Flumerfelt, and A. Alves (Eds), “Trans-Disciplinary Perspectives on System Complexity,” pp. 85-114, Springer, 2016.
[16] R. Rosen, “Anticipatory Systems - Philosophical, Mathematical and Methodological Foundations, Second Edition” Springer, 2012.
[17] D. M. Dubois, “Computing Anticipatory Systems with Incursion and Hyperincursion,” in Computing Anticipatory Systems: CASYS - First International Conference, edited by D. M. Dubois, AIP Conference Proceedings 437, pp. 3-29, American Institute of Physics, 1998.
[18] J. Cheng, “Temporal Relevant Logic as the Logical Basis of Anticipatory Reasoning-Reacting Systems,” in Computing Anticipatory Systems: CASYS 2003 - Sixth International Conference, edited by D. M. Dubois, AIP Conference Proceedings 718, pp. 362-375, American Institute of Physics, 2004.
[19] J. Cheng, Y. Goto, and N. Kitajima, “Anticipatory Reasoning about Mobile Objects in Anticipatory Reasoning-Reacting Systems,” in Computing Anticipatory Systems: CASYS 2007 - Eighth International Conference, edited by D. M. Dubois, AIP Conference Proceedings 1051, pp. 244-254, American Institute of Physics, 2008.
微信公众号“数理逻辑与哲学逻辑”
https://blog.sciencenet.cn/blog-2371919-1416702.html
上一篇:《纽约时报》起诉 OpenAI及MS 案件的社会影响
下一篇:也谈“新型研究型大学应该怎么办?”