博文
概率论真有频率论与贝叶斯论之分吗?(1)
|
概率论真有频率论与贝叶斯论之分吗?(1)
武汉大学 叶晓明
我翻过多本概率论与数理统计教材,都没有从中发现频率论与贝叶斯论的区分说。我观察发现,概率的频率解释主要集中在测量学界,把概率解释成客观频率。
我是反对这种分类的。概率是对未知事件的主观判断,主观判断依赖主观经验,主观经验来源于对客观频率统计资料的掌握。客观是手段,主观是目的,不存在学派分类问题。譬如:一个孕妇肚子里的胎儿的性别是个未知数,是个随机变量,我们会说这个胎儿的性别为男女各占50%的概率(可能性),这是因为我们掌握的人口性别的统计资料为男女各占一半。并不是说胎儿的性别客观上处于随机变化状态,也不是说该孕妇当天重复生无穷个孩子会出现男女各占一半。这无关频率论和贝叶斯论的分类问题。
测量学界主张频率论是因为它是基于歪曲的数学概念而解释,论据如下。
首先,请看它的典型测量结果表达,如:Z=20和σ(Z)=1.3。把Z=20代入到σ(Z)=1.3之中就得到等式σ(20)=1.3。这样,我们至少可以得到以下结论:
1、 这里的σ(Z)=1.3的实际数学含义是σ(20)=1.3。
2、 σ(Z)=1.3违反了数学概念σ2(C)=0。
3、 “相同测量条件下重复测得值的发散性”概念是通过偷换σ(Z)=1.3的实际数学含义σ(20)=1.3而臆造出来的测量概念。
4、 整个经典测量理论都是基于这种臆造偷换出来的测量概念而构建,即,重复测量的发散频率概念根本没有数学表达基础。
5、 这种偷换出来的“相同测量条件下重复测得值的发散性”概念同时又违反了数学上的方差概念,因为数学上的方差来自于随机试验样本的统计,随机试验对应于随机条件或所有可能条件而根本不是“相同条件”。
其次,再请看传统经典测量理论的基本概念原理图。
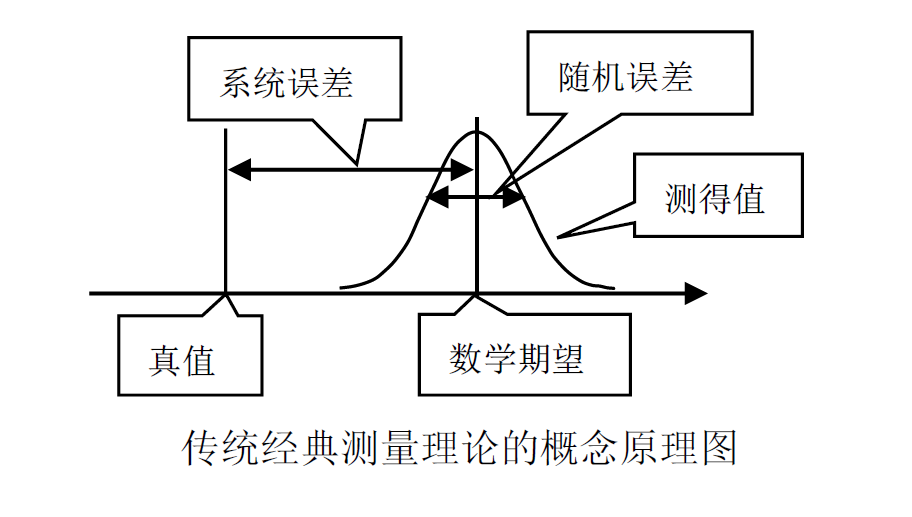
测得值Z=20是一个数值,其在数轴上应该表达为一个固定的点,可经典测量理论却把它当做变量,用一根概率曲线来描述它;真值是未知数,没有具体数值,应该视为变量、用概率曲线来表达其存在概率范围,可经典测量理论却又反而用一个固定点来表达它。就是说,经典测量理论违反了数学上的常数和变量概念,包括随机变量概念。
总之,经典测量理论违反了数学概念,这一所谓的频率学派是建立于违反数学概念和偷换概念的基础之上,以这样的“概念”为基础讨论概率论的学派分类当然是一个无聊的争论。
2024 2 4
参考文献
[1] 叶晓明 凌模 周强 王为农 箫学斌, 误差理论的新哲学观.计量学报 , volume 36, 2015, 6, Pages: 666-670.
[2] X-M. YE, H-B LIU, M. LING, X-B. XIAO, The New Concepts of Measurement Error's Regularities and Effect Characteristics. Measurement, Volume 126, October 2018, Pages: 65-71.
[3] X-M. YE, X-B. XIAO, J-B. SHI, M. LING, The New Concepts of Measurement Error Theory. Measurement, Volume 83, April 2016, Pages: 96-105.
[4] X-M. YE, S-J. DING, Comparison of Variance Concepts Interpreted by Two Measurement Theories. Journal of Nonlinear and Convex Analysis, Volume 20, Number 7, 2019, Pages: 1307-1316.
[5] H-S. SHI, X-M. YE, C. XING, S-J. DING, A New Theoretical Interpretation of Measurement Error and Its Uncertainty. Discrete Dynamics in Nature and Society, 2020. DOI: https://doi.org/10.1155/2020/3864578.
[6] H-S. SHI, X-M. YE, C. XING, S-J. DING, Origin and Evolution of Conceptual Differences between Two Measurement Theories, Fuzzy Systems and Data Mining VI, 2020, Pages:66 -77.
[7] H-B. LIU, X-M. YE, J-B. LIU, S-J. DING, Mathematical Concepts of Numerical Value and Variable in the Interpretation of Measurement Theory, Journal of Nonlinear and Convex Analysis, Volume 23, Number 9, 2022, Pages:2021-2034.
[8] 叶晓明丁士俊 师会生. 测量误差理论的真值中心论与测得值中心论. 计量科学与技术, 2021, 65(3): 19-27. doi: 10.3969/j.issn.2096-9015.2021.03.04
[9] X-M. YE, Robust Estimation Method Using Successive Approximation Algorithm to Correct Errors. Frontiers in Artificial Intelligence and Applications, 2022, 363, Pages:518-532.
[10] H-B. LIU, X-M. YE, S-J. DING. Weights Allocation for Optimal Uncertainty Evaluation. Journal of Nonlinear and Convex Analysis, Volume 24, Number 6, 2023, Pages:1177-1195.
[11] X-M. YE, Measurement Error Theory Based on New Concepts. Hubei Science and Technology Press, 2017.
https://blog.sciencenet.cn/blog-630565-1420518.html
上一篇:相信科学还真不是个简单的事
下一篇:概率论真有频率论与贝叶斯论之分吗?(2)