博文
不同考分的学生数服从BETA分布?
|||
不同考分的学生数服从BETA分布?
张学文,20170708
由很多学生参加的统一命题,判卷的考试得分,可以形成一个比较大的数据。从中不能统计出不同分数的学生各有多少。于是以分数为横坐标,以学生数量为纵坐标就可以获得一个关系曲线。我国每年的高考都可以形成这样一个大样本的权威分布(分数-学生数关系)函数。
我多年来一直希望分析这种数据,但是我无法获得这种数据。但是最近在姬揚的博客http://blog.sciencenet.cn/home.php?mod=space&uid=1319915 提示下,从http://www.bjeea.cn/html/zkzz/tzgg/2017/0702/66996.html
处获得的北京今年中考的分数与学生数量的北京各个区的数据,我认为这些数据可以分析这个问题。于是我把它们汇总为北京的总的学生人数与考分关系图。
下面是对应的图。
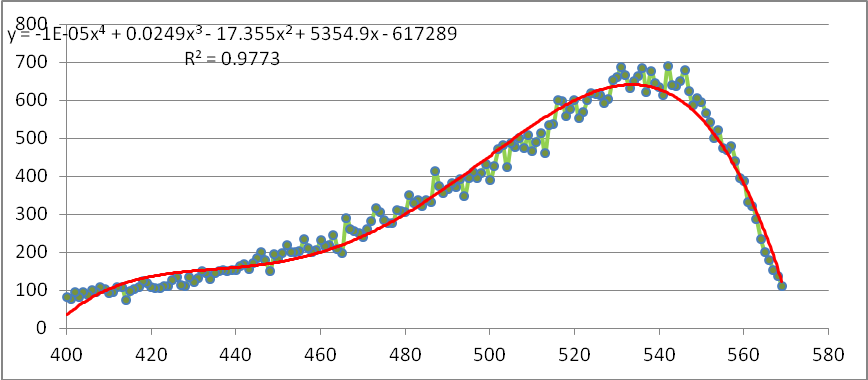
图中的横坐标是学生获得的分数,纵坐标是获得该分数的学生的数量(人数)。从中我们可以看到成绩与人数是一个单峰曲线。应当说在大样本的学生数基础上获得的曲线是平滑的(有规律性的,我为它配了4次多项式方程)。这让我们认可这些统计数据的合理可信。但是我们是否有能力追问,为什么考试成绩的统计特征会是这样,而不是过去某些人认为的,对称的正态分布?
我曾经认为说考试成绩服从正态分布的说法没有坚强的物理依据。而偏态的有一个最大值的分布是很有可能的。
为什么?
我过去的一个知识点就是,如果随机变量(现在值学生考试分数)其代数平均值为常数,并且(这一点很重要)其几何平均值也是常数,在最随机、最任意、最混乱,熵最大的情况下,随机变量取不同值的出现概率(百分比,比率)分布函数就是一个偏态的gamma分布(概率分布的一种)。
以上是我过去的一个猜想。
现在有了这个具体例子,看到它是偏态分布,我很高兴。
但是这个分布是向右侧的偏态让我感到别扭。
我又翻我2003出版的组成论一书。发现说它是BETA分布可能更合理(而不少我先前猜的GAMMA分布)。
为什么?
在最大熵、最复杂、概率最高的要求的同时,如果变量(考试分数)的几何平均值不变,而且变量有上限,那么它只能是BETA分布(见组成论一书192页)。
难道中国的考试具有这两个约束?
想一想,确实!首先我们的考试分数其实是个相对量,它不体现学生有多少知识,仅体现在很多学生的比较中,某学生的相对地好一些或者差一些。
另外,我们的考试分数是有上限的。即最高分是有上限值的(本例是580分)。所以最高分不得高于580分,而且分数是个相对意义的量。这两个考试分数(量)特点对应着最大熵分析中的两个数学约束条件。由此,考试成绩与学生人数的关系很类似BBETA分布也就很自然,合理了。
所以我现在的判断是这种考试的统计分布应当服从BETA分布是因为随机变量无形中存在两个约束与BETA分布要求的两个条件比较一致,而在最大熵(最可能,最任意)的情况下,它只能是BETA分布。
遗憾的是我现在没有耐心具体验证这个分布是否满足BETA分析了。我仅是利用excel 的软件轻易的弄了个类似BETA分布的多项式。欢迎有人具体进一步证实它就是符合BETA分布。
https://blog.sciencenet.cn/blog-2024-1065282.html
上一篇:昨天重庆奉节暴雨119.2毫米(20170708)
下一篇:昨天湖北鹤峰暴雨240毫米(20170709)
全部作者的精选博文
- • 漫话空中水
- • 大规模调水对降水的影响的旁例分析
- • 感谢许局长为我的书写了序言
- • 乌鲁木齐地震了!
- • 悼丁裕国教授!
- • 我的同学因为天气预报错误而判刑!