计算机科学家将两种“美妙”的证明方式融为一体

三位研究者构想出新的证明方式，既可以让信息散布开来，又绝对保密。

Ben Brubaker 著

左 芬       译

【译注：原文2024年10月4日刊载于QuantaMagazine，链接见文末。】

如何证明某件事情是真的？对于数学家来说，答案很简单：从一些基本假定出发一步步往前推进，直到结论。QED，也就是证明完成。如果某个地方有错，仔细阅读证明的专家会找到它。如果没有，证明就一定成立。数学家们遵循这一基本方式已经远远超过2000年了。

接着，在1980和1990年代，计算机科学家们重新构想了证明的可能形式。他们发展了令人眼花缭乱的种种新方式，而当尘埃落定时，两种创新尤其引人注目：零知识证明（zero-knowledge proofs），可以让一个怀疑者确信一个命题是对的而无需透露其原因；以及概率性可检验证明（probabilistically checkable proofs），可以在阅读者只看见少量片段时让其信服证明的真实性。

“在我看来，二者都可以跻身于整个理论计算机科学中最优美的概念，”剑桥大学计算机科学家Tom Gur称。

很快研究者们就开始尝试将这两种证明类型结合到一起。他们在1990年代后期获得了部分成功，但对每个条件都采用了稍弱的版本。数十年来，没有人能将零知识的理想化版本和概率可检验性的理想化版本融合到一起。

现在不同了。在七年努力铸成的一篇巅峰之作里，Gur和另两位计算机科学家最终在一类重要问题里将这两类证明的理想化版本结合到了一起。

“这一成果极其重要，”理论计算机科学家与StarkWare公司创始人，零知识证明的加密应用发起者Eli Ben-Sasson说，“它解决了一个非常古老且知名的未解难题，而这一难题困惑了研究者们很长一段时间，也包括我在内。”

请检验吧

故事开始于1970年代早期，那时计算机科学家开始形式化地研究他们让计算机解决的问题的困难程度。这些问题大多享有一条重要性质：如果有人找到了一个有效答案，很容易让一个持怀疑态度的“验证者”信服它确实可行。反过来，如果有错误的话，验证者总是很容易找出来。具有这一性质的问题归属于研究者称为NP的一个类别里。

自上往下，Shafi Goldwasser, Silvio Micali与Charles Rackoff，他们发明了零知识证明，其无需揭露原因即可证实一个命题为真。

为了理解这种验证如何实施，考虑一个古典的NP问题：给定划分成不同区域的一张地图，是否可以只用三种颜色填充它，使得相邻区域颜色不同？取决于地图，这一问题可能难乎其难。但如果你设法找出了一种合理着色方式，你只需要向验证者展示着好色的地图，就可以证明它是对的。验证者只需要看一眼所有的边界就行了。

十年后，两个研究生倡导了看待数学证明的一种另类方式。同在加州大学伯克利分校的Shafi Goldwasser与Silvio Micali一直纳闷是否可以在线上扑克游戏中防止欺诈。大体来说这需要证明每个玩家手上的牌是随机抽取的，但又不能透露出这些牌是什么。

在1985年与多伦多大学计算机科学家Charles Rackoff合著的一篇开创性论文中，Goldwasser和Micali发明了零知识证明，给他们自己的问题一个响亮的肯定回答。第二年，Micali与另两位研究者在一篇跟进的文章中表明，任何NP问题的答案都可以用一种特定类型的零知识证明予以验证。

要对这些证明有所了解，仍然假定你想让验证者信服一张特定地图是可以三着色的——不过这一次，你不想让验证者本人知晓着色方式。你不再画出实例，而是通过一种互动式过程来证明它。首先给地图着色，接着用黑布条把所有区域都盖上，只让所有边界可见。验证者接着随机选中一条边界，而你会打开两边的区域，露出两种不同颜色。

接着重复这一过程多次，并在每一轮之前都随机地切换颜色模式，使得验证者无法拼凑出关于你的答案的任何连续信息。（例如，交换红色与蓝色区域，且保持绿色区域不变。）如果你是在诈唬，验证者总会发现一个地方的着色不合理。如果你说的是真的，你总可以在跟标准证明方式差不多的时间里让他们在合理范围内信服。

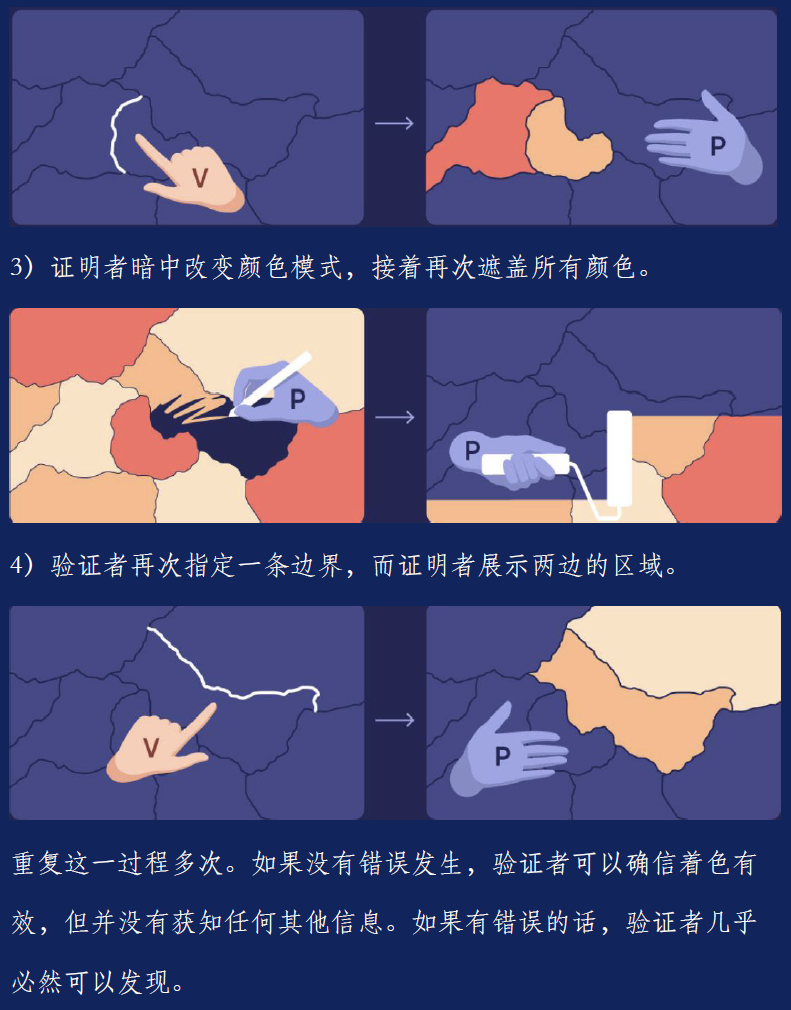
这一零知识证明与标准证明方式在两个地方显著不同：它是一个互动式过程而非一个文件，并且每个参与者都依赖于随机性来确保另一个无法预测其决定。但正由于随机性，这里始终存在一定几率使得一个有瑕疵的证明被视为成立的。当然，很容易让这一几率变得极其之小，因此计算机科学家们很快就把对这一松散证明定义的不快抛诸脑后了。

正如加州大学洛杉矶分校的计算机科学家Amit Sahai所言，“如果某个命题不对的概率比宇宙中粒子总数分之一还小，我们觉得把它当成对的大概是合理的。”

酷炫的证明

研究者们很快意识到随机互动式证明的能力远不止是隐藏私密信息。它们还可以轻松验证比NP难得多的问题。有一种互动式证明甚至还对所谓NEXP类里的所有问题适用。而利用常规证明，仅仅验证这些问题的解就需要解决最难的NP问题那么久的时间。

证明方式的变革最终在一个惊人的发现中达到了巅峰：即使没有任何互动，你仍然可以获得互动式证明的全部威力。

原则上，移除互动是很直接的。“证明者列出他可能从验证者那里得到的所有可能挑战，然后提前写出他的所有答案，”Sahai说。问题是对于NEXP里最难的那些复杂问题，生成的文本会是巨大无比的，要从头到尾读完根本不可能。

接着在1992年，计算机科学家Sanjeev Arora和Shamuel Safra定义了一类全新的非互动式证明：概率性可检验证明（Probabilistically Checkable Proofs），简称PCP。与其他研究者一道，他们证明NEXP问题的任何答案都可以用这种特殊形式写出来。尽管PCP要远远长于常规证明，验证者可以通过只阅读小的片段来实现严格审查。这是因为，PCP会把常规证明中的任何错误都放大并散布开来。在常规证明中找错就好像是咬一片吐司来找一小团果酱。PCP“把果酱均匀地涂抹在整片面包上，”Gur说，“无论从在哪里咬都没关系，你总会发现它。”

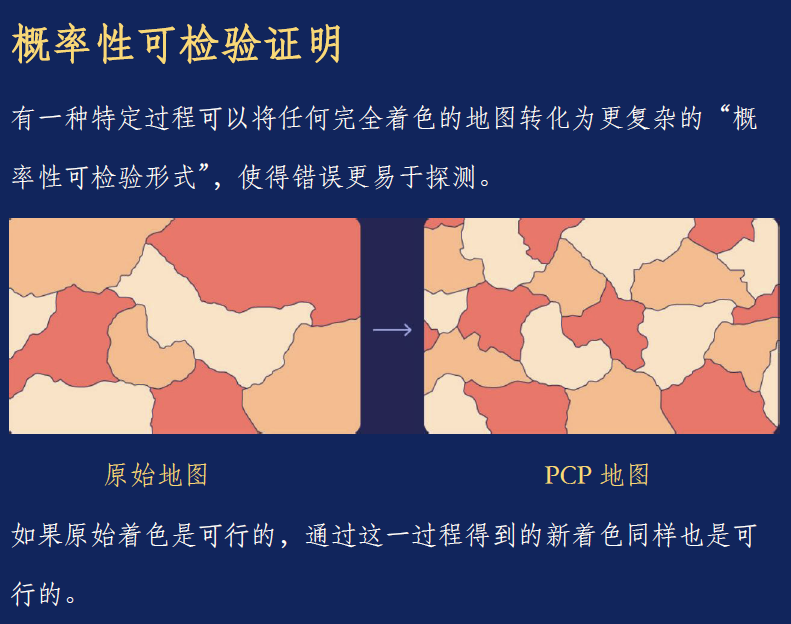
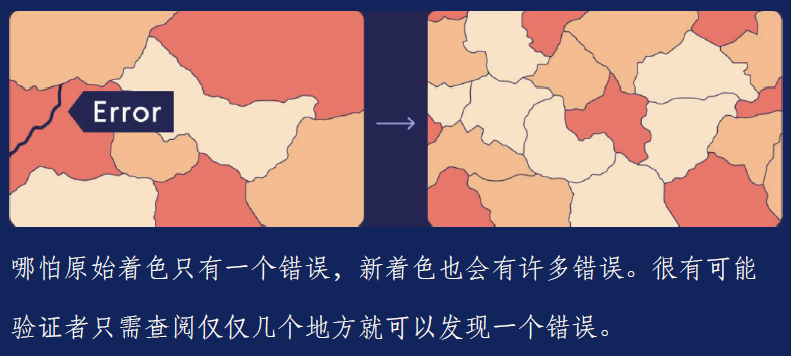
关键因素又是随机性——验证者的片段选择必须是不可预见的，以确保不诚实的证明者无法在任何地方隐藏矛盾之处。

Arora, Safra和合作者证明，对于更常见的NP问题，PCP还可以大幅加速验证过程。紧接着，Arora和另外四位研究者进一步改进了PCP，将NP证明验证的速度推进到理论极限——这就是声名远播的PCP定理。

“这被认为是理论计算机科学中的伟大成就之一，”海法市以色列理工学院的密码学者Yuval Ishai说道。

通往PCP定理的道路绝非平坦的。研究者们从针对NP问题的既使用互动性，也使用随机性的零知识证明开始。接着他们意识到类似的证明可以用于验证难得多的问题的答案。最后他们证实，将这些证明转化为非互动式的PCP之后，验证答案的时间比直接阅读证明要少得多。计算机科学家们感到大获全胜。

1990年代，Sanjeev Arora和其他研究者找到了构建概率性可检验证明的方法，使得验证者只需要阅读少量片段就可以完成审查。

不过，在后续的一些年里，一些研究者开始考虑在这一过程中什么被丢失了。结果表明，将证明转换成PCP暴露了零知识证明意图隐藏的部分信息。有没有什么方法可以让二者都达到最佳效果呢？

信息爆炸

不幸的是，在概率可检验性和零知识之间存在着一种内在的矛盾。这一麻烦起源于PCP的非互动本质。常规零知识证明依赖互动性来限制验证者获取机密信息。非互动式证明只是证明者交给验证者的一个文件，后者可能更想窃取前者的秘密，而非审查答案。

“这并非简单地把他们要看的特定部分伪装起来，”剑桥大学跟Gur一同发现最新结果的一名研究生Jack O’Connor说，“我们得把证明全盘伪装好，无论他们以什么方式检查它。”

如果验证者可以从头到尾直接读完证明，就不可能实现零知识（除非你假定特殊类型的加密方式是不可破解的。）于是，研究者们把构造PCP的零知识版本的目标聚焦在超出NP的极难问题上，因为这些PCP仍然是可以验证的，但已经长到没法全盘读完了。这些零知识的版本必须把信息散布到证明的每个部分以确保证明者的诚实，同时又得确保证明除了其正确性之外不泄露任何信息，无论验证者阅读的是哪些片段。

1997年，三位研究者战胜了这些挑战，构造出一种对NEXP中的任何问题都适用的零知识PCP——但付出了一定代价。他们不得不在验证者审查证明时找补回一点互动性——这跟通常的PCP情况相悖，因为那里没有什么是互动式的。

“你先去看一眼，接着想一想，然后再回到它去读另一个部分，”Sahai说。在常规PCP里，“你可以一开始就决定想要读证明的哪一小部分。”

这一结果还用到了零知识的一种不太完美的形式，因为有微小的非零几率被验证者获知一些额外信息。这对于零知识证明在加密中的所有实际用途已经足够好了。但一些研究者仍执着于“完美零知识”——哪怕使用互动式证明，也并不总能实现的一个苛刻条件。

绝对保密

在接下来的20年里，几个研究者改进了1997年那篇文章的方法，使得零知识PCP在加密实践中更加有用。但根本的局限性仍然存在。接着在2017年，伯克利一名叫Nicholas Spooner（如今在康奈尔大学）的研究生开始猜测他在另一个相关问题上协助发展的技术可能对构建完美零知识PCP也有用。

Spooner把想法抛给了Gur，那时在伯克利做博士后。Gur不太相信，并花了接下来的一年时间去证明它无法实现。但有一天早上在伯克利的一家咖啡馆里Spooner向他展示了一个小技巧，可以用来排除新方法中最显眼的障碍，于是他改变了主意。

从左到右：Tom Gur, Jack O’Connor与Nicholas Spooner。他们构建的证明方式结合了零知识的理想版本与概率可检验性的理想版本。

“我有点悲观主义，而他更乐观，”Gur说，“他赢了。”

两位研究者聚焦于关于NP问题解的数目的“计数问题”，例如，“给定一张地图，可能存在多少不同的可行解？”有一套标准的流程来构建此类问题的PCP，需要用到巨大的多维数据表格，而验证者可以加和某些条目来获知答案，并且加和其它条目来检验证明者是否保持诚实。可是这些个体数据的值会透露额外信息，因此这些PCP并非零知识的。在Spooner的新方法中，证明者会在表格中引入随机性来隐藏这些值，而验证者可以检验这一随机性并不改变最后的求和。

Gur和Spooner一起断断续续地研究了五年多，但始终没办法把细节都厘清。2023年O’Connor加入了小组，因为他们仨意识到关键的缺失因素可能在他们一同参与的另一篇看似无关的论文中找到。在这个秋天的最后一次齐心协力后，三位研究者终于在他们的新文章中把所有片段都整合到了一起。其结果就是针对所有计数问题的一种完美零知识PCP。此外，这些PCP的验证过程还是完全非互动式的。

“他们一次性地突破了双重障碍，”Ishai称，“我被彻底震惊了。”

Spooner, Gur 和 O’Connor研究的是计数问题归属于一类被称作#P（读作“升P”【译注：#P的中文读法似乎没有共识。译者这里从音乐领域借用了升降调的读法。】）的问题，它们在难度上介于NP和NEXP之间。三位研究者现在试图将他们的新技术加以推广，应用到NEXP中的所有问题，以与Arora和Safra原始文章中PCP的威力相当。这将会是很大的一步，相当于要在完美零知识的额外收益下，证明原始PCP定理的的某种等价物。Gur对此感到乐观，因为他们的新方法等同于在PCP定理中起关键作用的一种技术的零知识版本。

新的证明方式往往会在计算机科学的其它分支找到应用——这也是研究者们对这一新工作感到激动不已的另一个原因。

“对零知识PCP的热潮极有可能就此复生，”Ishai说，“这会导致理论计算机科学的其它进展。”证明，将重现无尽可能。

原文链接：

https://www.quantamagazine.org/computer-scientists-combine-two-beautiful-proof-methods-20241004/