计算机科学家拓展可验证知识的疆域

在量子纠缠这一秘密武器的加持下，计算机可检验问题的王国不断扩张。

Kevin Hartnett 著

左    芬     译

【译者按：这是MIP^*=RE 定理最终得以证明的关键一步。对该工作，Thomas Vidick有一个非常简洁的评价：“随机性与交互带给我们一个指数因子[的提升]；纠缠带给了我们另一个。”（详见其博文“Randomness and interaction? Entanglement ups the game!”）

原文2019年5月23日刊载于QuantaMagazine，链接见文末。】

通过讯问纠缠的量子计算机，你可以验证极其复杂问题的答案。

假如有人走过来告诉你，他拥有一则神谕，能用它揭示宇宙最深奥的秘密。尽管你很好奇，但却难以相信。你想要有某种方法可以验证神谕告知你的确实是真的。

这正是计算机科学中核心问题之一的关键所在。有些问题难到根本无法在合理的时间段内解决。但它们的答案却易于检验。在此前提下，计算机科学家想要知道：答案始终可以验证的问题能难到什么程度？

最终的回答是：难到你几乎无法想象。

在今年四月公布的一篇文章中，两位计算机科学家显著地增加了属于难解易证这一范畴的问题数目。他们给出了一种方法，可以用它验证的问题能拥有几乎无法想象的复杂性。“看上去有些疯狂，”加州理工学院计算机科学家Thomas Vidick说。他没参与到这一新工作中。

这一研究适用于量子计算机——依据量子力学反直觉的规则来执行运算的计算机。量子计算机现在还几乎不存在【译注：这里提醒一下，本文发表于2019年5月。】，但未来有可能带来计算的变革。

新工作本质上给了我们与全能神谕进行周旋的手段。哪怕神谕允诺回答的问题求解起来远远超出你自己的能力，仍然有一种办法确保神谕说的是对的。

直到宇宙终结

当一个问题难于解决但易于验证时，找到解要花很长时间，但验证给定解是对的则不需要。

例如，设想有人给了你一个图——由一些线（边）连接起来的点（顶点）的集体。他问你是否可以只用三种颜色给图的顶点着色，使得任两个连着的顶点颜色都不同。

在三色图中，每个顶点用三种颜色之一着色，且任两个相连的顶点颜色均不同。

这一“三色”问题难以解决。一般来说，找到一个图的三着色方法（或者判定其不存在）需要的时间随着图的增大而指数式地增长。例如，对于20个顶点的图，找到解需要3²⁰纳秒——大约几秒钟——而60个顶点的图需要大约3⁶⁰纳秒，也就是差不多宇宙年龄的一百倍。

可是，设想有人声称已经给一个图进行了三着色。要检验他们的结果是否是对的花不了多长时间。你只需要挨个遍历顶点，检查它们的关系。当图变大时，完成这些所需的时间增长得很缓慢，以所谓多项式方式增长。因此，计算机检验60点图的三着色花费的时间比检验20点图长不了多少。

“给定一个像样的三着色，检验它是否可行很容易，”麻省理工学院的物理学家John Wright说道。他与加州理工学院的Anand Natarajan合写的这篇新文章。

1970年代，计算机科学家定义了易于验证但可能难于求解的问题的类别。他们称这一类别为“NP”，用以指代非确定性多项式时间（Nondeterministic Polynomial time）。在那之后，NP一直是计算机科学中研究得最密集的问题类。特别地，计算机科学家们想要弄清，当你给予验证者新的方法去检验答案真伪时，这一类别会如何改变。

恰当的问题

在Natarajan和Wright的工作之前，验证能力已经有过两次巨大的飞跃。

要理解第一次飞跃，假设你是色盲。有人把两块积木放在你面前的桌子上，问你它们颜色是否相同。这是个你无能为力的任务。此外，你也没法验证其它人的答案。

现在允许你讯问这个人，也就是我们所谓的证明者。假定证明者告诉你两块积木的颜色是不同的。你把一块积木记为“积木A”，另一块记为“积木B”。然后你把积木放到背后，在两只手中随机交换。接着你把积木拿出来，让证明者指出积木A。

如果积木颜色不同，这个测验就再简单不过了。证明者知道积木A是比如说红色，会每次都正确找到它。

但如果积木其实颜色相同——意味着证明者诈称它们颜色不同——那么证明者就只能猜测两块积木分别是哪块。这样一来，证明者就只有50%的可能性指出积木A。通过不断试探证明者的答案，你就能验证其是否正确。

Anand Natarajan（左）与John Wright在他们的新工作中利用了量子力学。

“验证者可以提出恰当的问题，”Wright说道，“或许到了对话结束时，验证者会更加信服。”

1985年三位计算机科学家证明，这样的交互式证明能用来验证比NP类更加复杂的问题的解。他们的工作创建了一种新的问题类，所谓IP，意指“交互式多项式（Interactive Polynomial）”时间。用来验证两块积木颜色的相同方法于是可以用来验证复杂得多的问题的解。

第二个主要进展发生在同一时代。它遵循了警察调查的同一逻辑。如果你认为在一个案子里有两个嫌疑人，你是不会一起质询他们的。相反，你会在不同的房间里讯问他们，并把一个人的答案跟另一个人的进行比对。通过分别盘问他们，你可以揭示比只有一个嫌疑人可以讯问时更多的真相。

“[两个嫌疑人]没法形成某种自洽的共同故事，因为他们根本就不知道另一个人给了什么样的答案。”Wright称。

1988年四位计算机科学家证明，如果你让两台计算机分别解决同一问题——并就它们的答案分别讯问它们——你可以验证一类远远超出IP的问题：所谓MIP，意指多方交互式证明（Multi-Prover Interactive proofs）。

例如，有了多方交互式方法，就可以验证比NP情况下规模增长得更快的图序列的三着色。在NP里，图的大小以线性速率增大——顶点数目可能从1到2，到3，再到4等等——从而始终不会与验证其三着色所需时间显著地不相称。但在MIP里，图的顶点数呈指数地增长——从2¹到2²，到2³，再到2⁴，等等。

结果，图很快就大到在验证者的电脑存储器里放不下了，于是它没法遍历顶点列表来验证三着色。但通过询问两个证明者不同但相关的问题，仍然可以对三着色进行验证。

在MIP里，验证者的存储器足够用来执行一个程序，对这样的图中的两个顶点之间是否有边连着进行判别。验证者接着让每个证明者说出两个相连顶点之一的颜色——然后它可以对证明者的答案进行交叉比对以确保三着色可行。

难以解决但易于验证问题从NP到IP再到MIP的扩展涉及的是经典计算机。量子计算机的工作原理完全不同。数十年来人们并不清楚它们会怎么改变这一格局——它们会使得答案的验证更加困难还是更加容易呢？

Natarajan与Wright的新工作给出了回答。

量子欺骗

量子计算机通过操控量子比特，也叫量子位，来进行运算。它们拥有一种神奇的性质，就是可以相互纠缠起来。当两个量子比特——甚至大型量子比特体系——纠缠着时，意味着它们的物理性质会以某种方式相互对抗。

在他们的新工作中，Natarajan与Wright考虑了共享纠缠量子比特的两台远离的量子计算机这样一种方案。

这种架构看起来似乎与验证背道而驰。多方交互式证明的威力就在于你可以分别讯问两个证明者，并交叉比对他们的答案。如果证明者的答案是自洽的，则很可能他们是对的。但共享纠缠态的两个证明者似乎有了更大的能力来自洽地维护不正确的答案。

确实，当两台纠缠量子计算机这一方案在2003年首次提出时，计算机科学家认为纠缠会削弱验证能力。“包括我在内的所有人的显然反应时，现在你给了证明者更多能力，”Vidick说，“他们可以利用纠缠来协同他们的答案。”

尽管最初有些悲观，Vidick花了数年时间试图证明事情并非如此。2012年，他和Tsuyoshi Ito证明，使用纠缠的量子计算机仍然可以验证MIP里的所有问题。

如今Natarajan和Wright证明情况甚至更好：在有纠缠的情况下能验证的问题类别比没有时要大得多。有办法把纠缠量子计算机之间的联系转向对验证者有利的一面。

“他们遗留了这种可能性：另一个飞跃有望出现。”

                                       —— Lance Fortnow

要看出这一点，回顾一下在MIP中验证规模指数增长的图的三着色的流程。验证者无需足够存储来存下整个图，而只需足够存储来判别两个相连顶点，并询问证明者这些顶点的颜色。

而对于Natarajan与Wright考虑的一类问题——所谓NEEXP，意指非确定性双重指数时间——图的规模比在MIP里增大得更快。NEEXP里的图以“双重指数”的速率增长。图中的顶点数目不再以2的幂次增长——2¹,2²,2³,2⁴等等——而是以2的幂次的幂次增长——等等。因此，图很快就增长到验证者甚至无法判别一对相连顶点了。

一个问题有多难？

     研究者使用计算类别的一个嵌套集合来划分所有问题的王国。

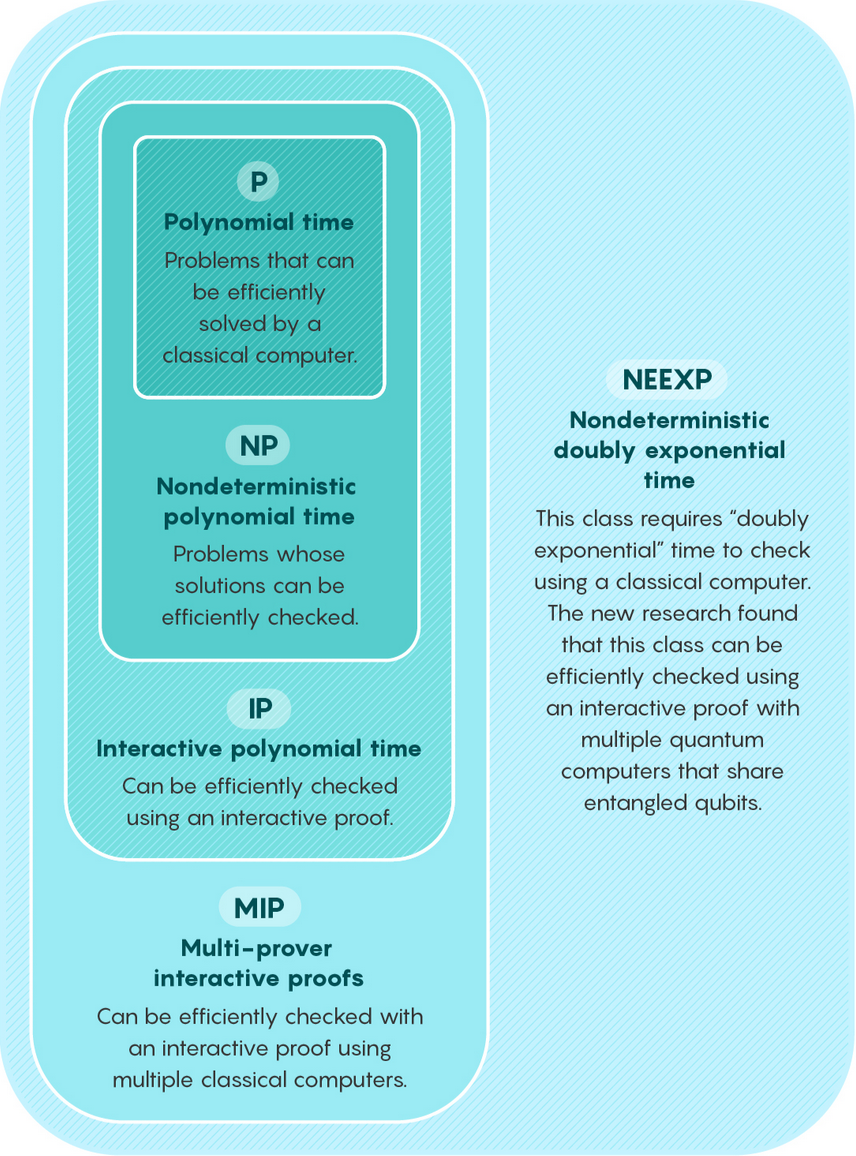
P 多项式时间 可以用经典计算机有效解决的问题。

NP 非确定性多项式时间 解可以有效检验的问题。

IP 交互式多项式时间 可以使用交互式证明有效检验。

MIP多方交互式证明 可以使用多台经典计算机组成的交互式证明来有效检验。

NEEXP非确定性双重指数时间 这一类别使用经典计算机来检验需要“双重指数”时间。新研究发现，使用共享纠缠量子比特的多台量子计算机组成的交互式证明可以有效检验这一类别。

“标记一个顶点就需要2ⁿ个比特，而这比验证者拥有的工作存储要大指数倍，”Natarajan称。

但Natarajan和Wright证明，即使无法指出要询问证明者的顶点，仍然可以验证双重指数大小的图的三着色。其原因在于你可以让证明者自己提出问题来。

让计算机进行自我讯问的这一想法，在计算机科学家看来，就跟让犯罪嫌疑人自我讯问一样荒谬——离谱得不能再离谱了。可Natarajan与Wright证明并非如此。原因就在于纠缠。

“纠缠态是一种共享资源，”Wright说，“我们的整个协议就是去弄清楚如何利用这一共享资源来生成相关的问题。”

如果量子计算机是纠缠的，那么它们的顶点选择也会是相关的，从而正好产生验证三着色的恰当问题集。

与此同时，验证者并不希望两台量子计算机过分交织，以致它们对这些问题的答案也相关（等同于两个犯罪嫌疑人协同他们虚构的不在场证明）。另一条奇怪的量子性质消除了这一忧虑。在量子力学中，不确定性原理阻止我们同时知晓一个粒子的坐标和动量——如果你测量一种属性，就会破坏关于另一种属性的信息。不确定性原理严格地限制了你对一个量子系统所能知晓的任意两种“互补”属性。

Natarajan和Wright在他们的工作中利用了这一点。为了计算顶点的颜色，他们让两台量子计算机执行互补的测量。每台计算机计算它自己顶点的颜色，而在此过程中，它会破坏关于另一顶点的任何信息。换句话说，纠缠允许计算机产生相关的问题，而不确定性原理阻止它们在回答时共谋。

“你得迫使证明者遗忘，而这就是[Natarajan和Wright]在他们的文章中主要做的，”Vidick说，“他们迫使证明者进行测量来擦除信息。”

他们的工作拥有近乎存在主义的影响。在这篇新文章之前，我们有确切把握支配的知识量的上限要低得多。如果我们收到NEEXP里一个问题的答案，我们别无选择，只能信以为真。但Natarajan和Wright大幅超越了那一上限，使得我们可以在一个更加辽阔的王国里对计算类问题的解进行验证。

不过在他们成功之后，验证能力的极限究竟何在仍不明朗。

“这还可以走得更远，”佐治亚理工学院的计算机科学家Lance Fortnow称，“他们遗留了这种可能性：另一个飞跃有望出现。”【译注：事后来看，这条评论堪称神预测。就在第二年，通过迭代Natarajan-Wright过程，包括Natarajan和Wright在内的五位研究者一同证明了MIP^*=RE定理，从而最终确定了纠缠证明者验证能力的极限。】

原文链接：

https://www.quantamagazine.org/computer-scientists-expand-the-frontier-of-verifiable-knowledge-20190523/