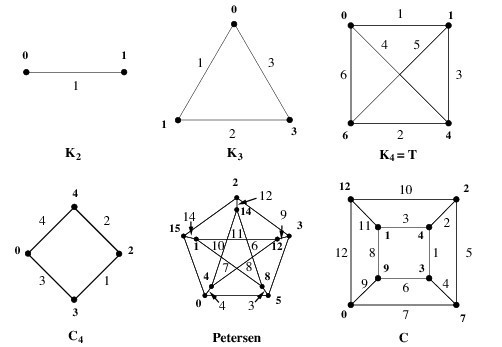
优美图：顶点标号在{0,1,...,e}中互不相同；边为顶点标号之差，且为{1,2,...,e}两两不同；形式化描述如：

  存在单射g:V(G)->{0,1,...,e}，使得映射g'（uv）=g（u）-g（v)是E（G）到{1,2，。。。，e}的双射；

1、优美图的优美标号可应用于代数编码理论、通信网络编址、射电天文学、导弹控制码设计同步、整电压发生器设计、雷达、密码设计、X射线衍射晶体学等；
2、1966年，Rosa猜想：所有的树都是优美图--著名的优美树猜想；但优美树至今没有得到证明或否定；
3、已经证明了的优美图：路、毛毛虫树、花树、对称树、橄榄树、最多有4个悬挂点的树、直径最多为5的树、最多有27个顶点的树等

 A labeled graph which can be "gracefully numbered" is called a graceful graph. Label the nodes with distinct nonnegative integers. Then label the graph edges with the absolute differences between node values. If the graph edge numbers then run from 1 to , the graph is gracefully numbered. In order for a graph to be graceful, it must be without loops or multiple edges.

Golomb showed that the number of graph edges connecting the even-numbered and odd-numbered sets of nodes is , where is the number of graph edges. 

 

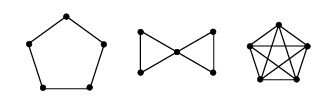
The only ungraceful simple graphs with nodes are shown above.

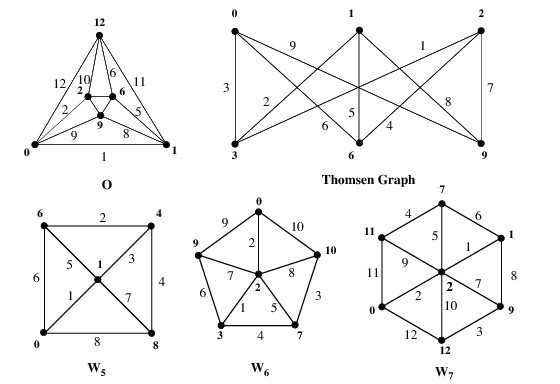
There are exactly graceful graphs with  graph edges (Sheppard 1976), where of these correspond to different labelings of the same graph. Golomb (1974) showed that all complete bipartite graphs are graceful. caterpillar; complete graphs , , (and only these; Golomb 1974); cyclic graphs  when , when the number of consecutive chords , 3, or (Koh and Punnim 1982), or when they contain a chord (Delorme et al. 1980, Koh and Yap 1985, Punnim and Pabhapote 1987); gear graphs; path graphs; the Petersen graph; polyhedral graphs , , , , and (Gardner 1983); star graphs; the utility graph (Gardner 1983); and wheel graphs (Frucht 1988) are all graceful.

Some graceful graphs have only one numbering, but others have more than one. It is conjectured that all trees are graceful (Bondy and Murty 1976), but this has only been proved for trees with graph vertices (Aldred and McKay 1998). It has also been conjectured that all unicyclic graphs are graceful.