博文

【论文推荐】带有输入饱和的非线性全驱系统级联预测控制

已有 155 次阅读 2026-1-13 11:27 |个人分类:论文推荐|系统分类:博客资讯

编辑荐语

本期将给大家分享"带有输入饱和的非线性全驱系统级联预测控制(Cascade predictive control for nonlinear fully-actuated systems with input saturation)". 如您对本期相关内容有好的理解与建议, 欢迎评论区留言.

本文针对输入饱和约束下非线性全驱系统的预测控制难题, 提出了一种创新的级联预测控制方法, 为解决传统全驱系统方法中因非线性输入变换而导致的强非线性约束问题提供了系统性的解决方案. 论文深入剖析了经典全驱预测控制在面对输入饱和时, 优化问题会重新退化为难以求解的非凸非线性规划这一核心矛盾, 并创造性地设计了双层级联优化结构: 上层通过引入线性边界优化, 将输入饱和约束转化为预测时域内的线性约束; 下层基于重构的线性约束求解带有松弛因子的分散式二次规划, 从而在严格保证输入与状态约束满足的同时, 显著降低了在线计算复杂度. 该方法不仅从理论上确保了闭环系统的稳定性, 而且通过全驱航天器姿态控制与欠驱动RTAC系统的仿真对比, 验证了其在控制精度、约束满足与实时性方面的综合优势. 本工作成功地将全驱系统理论与预测控制框架深度结合, 为具有复杂约束的高阶非线性系统控制提供了兼具理论严谨性与工程可实现性的新途径.

本文问题切入点精准, 方法设计巧妙, 所提出的级联优化架构有效破解了输入饱和约束带来的求解瓶颈, 在推动全驱系统预测控制的实际应用方面具有重要价值. 推荐给从事非线性控制、模型预测控制、全驱系统理论以及航空航天、机器人等领域控制方法研究的科研人员与工程师阅读参考.

论文介绍

带有输入饱和的非线性全驱系统级联预测控制

Cascade predictive control for nonlinear fully-actuated systems with input saturation

王秀博1,2†, 段广仁2,3

机构: 1. 东北大学秦皇岛分校控制工程学院; 2. 哈尔滨工业大学控制理论与制导技术研究中心; 3. 南方科技大学深圳市控制理论与智能系统重点实验室

引用: 王秀博, 段广仁. 带有输入饱和的非线性全驱系统级联预测控制. 控制理论与应用, 2025, 42(12): 2419 – 2428

DOI: 10.7641/CTA.2025.40297

全文链接:

http://jcta.alljournals.ac.cn/cta_cn/ch/reader/view_abstract.aspx?file_no=CCTA240297&flag=1

摘要

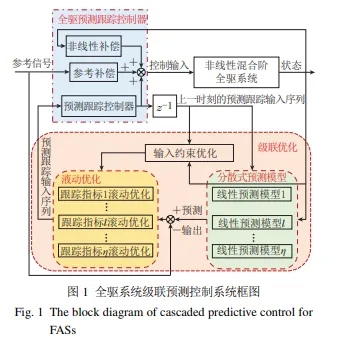
基于全驱系统方法的预测控制通过非线性输入变换, 将原始输入映射为期望的线性闭环系统输入, 进而构造分散式线性预测模型, 降低了优化问题求解的复杂度. 然而, 当系统具有输入饱和约束时, 此类输入变换为期望的预测模型引入强非线性的约束问题. 为此, 本文提出了一种级联预测控制方法, 设计了双层优化结构的级联预测控制器: 第1层优化结合上一时刻的预测输入序列, 优化预测时域内输入变换后的线性边界; 第2层优化则基于重新定义的线性约束, 求解带有松弛因子的分散式线性优化问题. 该方法有效避免了因输入变换引发的非线性约束问题, 降低优化复杂度, 并提高非线性优化问题的可解性, 同时保证闭环系统的稳定性. 最后, 通过对全驱航天器姿态系统和欠驱转动平移驱动系统的仿真, 验证了所提算法的有效性.

引言

预测控制起源于20世纪60年代, 因其显式处理多变量约束的优势已经迅速发展成为控制理论和工程应用中极为重要的一部分[1–2]. 预测控制广泛应用于化工和石油炼制、能源管理和电力、汽车工业、航空航天、机器人技术、水处理和环境工程、农业、医疗设备和健康监护等领域[3–7].

当前非线性预测控制主要基于一阶状态空间方法, 可分为3类: 基于线性化方法的预测控制通过对非线性系统线性化建立预测模型, 但存在局部线性化误差和适配性问题[8]; 基于人工智能的预测模型逼近方法利用神经网络和模糊控制等技术简化了模型复杂度, 但忽略了物理属性, 可能导致模型偏差[9]; 非近似的非线性模型预测方法提供精确预测模型, 但因非线性优化计算负担过高限制了实时控制效率, 且随着控制系统模型复杂度的提升, 预测控制中优化问题的求解变得困难[10]. 即使在无约束条件下, 通过变量增广得到的一阶状态空间预测模型也极其复杂, 随之导致优化问题的求解变得更加困难. 通常, 这需要投入大量的计算资源和时间来寻找最优的预测控制序列. 特别是在高维多变量系统或有限预测时域较长的情况下, 优化问题计算复杂度会显著增加[11]. 若进一步考虑系统的约束条件, 不仅优化问题的求解时间更长, 控制预测序列的求解可能无法满足实时控制要求, 导致系统性能下降或者不稳定, 甚至出现优化解不存在的情况[12]. 此外, 带有输入饱和约束的非线性预测控制问题通常会转化为一个难以求解的非凸优化问题.

非线性预测控制问题求解的瓶颈在于系统模型的复杂性. 通过变量增广将原始非线性系统转换为一阶状态空间, 复杂的非线性特征传递到预测模型和滚动优化问题中[13]. 然而, 状态空间模型并不是用来描述动态控制系统的唯一或原始形式. 在许多实际物理系统中, 根据牛顿定律、动量定理、拉格朗日方程、基尔霍夫定律等物理定律建立的系统模型通常是二阶的, 或被复合为高阶的或混合阶的[14]. 在进行控制系统设计时, 人们通常习惯性的将这些物理模型通过变量增广转换为一阶状态空间模型. 虽然状态空间方法对线性系统理论是完备的, 但其在处理非线性系统的约束和可控性问题上具有明显的局限性[15] .

不同于一阶状态空间方法, 全驱系统方法在控制系统的分析和设计中具有巨大的优势和潜力, 可以有效地降低控制设计中的复杂度, 进而获得更为完备、简单、通用的控制律表达式[14, 16]. 因此, 全驱系统方法的关键步骤是为所考虑的动力系统推导全驱系统模型. 一旦获得全驱系统模型, 利用系统的全驱特性可直接设计稳定控制器. 在现实的物理世界中, 根据基本物理法则(如牛顿运动定律、动量守恒定律和能量守恒定律等), 可以推导出广义的全驱系统模型, 并且高度自动化的系统模型通常是全驱系统特性的典型体现. 此外, 全驱系统方法的适用系统不限于传统的全驱系统. 在处理欠驱系统时, 现有文献克服了控制输入维度受限的问题, 通过诸如状态消元升阶或寻找同胚变换的方法, 能够将欠驱系统转化为全驱系统、包含自治子系统的复合全驱系统或亚全驱系统, 这在系统模型层面揭示了系统的可控性和内在的动态特性, 并为基于全驱系统控制理论实现预期控制目标提供了依据[17]. 在处理非完整系统时, 针对典型的非完整系统和以积分链形式存在的广义非完整系统, 基于全驱系统方法的亚全驱或非连续控制策略实现了对这些系统的有效控制[18].

与传统的预测控制方法相比, 全驱系统理论集成到预测控制中, 大大降低了优化问题的复杂性. 但值得注意的是, 在现有基于全驱系统方法预测控制文献[12–13, 19–20]中, 全驱预测控制器的通常表征为: u(k)=−B−1 (·)(f(·) − v(k)), 其中: B(·)和f(·)是与系统相关的非线性函数, v(k)是预测控制器. 可以看出, 系统输入u到预测跟踪控制器v存在非线性输入变换. 当全驱系统存在线性输入约束时, 在预测时域内经过此输入变换为期望的预测模型: x(k + i + 1) = Aix(k) + i ∑−1 j=0 AjBv(k + j)引入了强非线性输入约束, 进而解耦的线性优化问题将重新回归为耦合的非线性优化问题. 因此, 本文针对具有输入约束的非线性混合阶全驱系统, 提出了一种基于级联优化的预测控制方法, 在对参考信号进行跟踪的同时, 保证系统输入满足系统输入约束条件, 并通过对全驱航天器姿态系统和欠驱旋转平移驱动(rotational translational actuator, RTAC)系统的仿真, 验证了所提算法的有效性. 具体地, 本文的主要贡献概括为以下两点:

1) 级联优化: 设计一个采用双层优化的预测级联控制器. 在第1层优化中, 结合上一时刻的预测跟踪输入序列, 优化求解预测时域内经输入变换后的新输入约束线性边界. 在第2层优化中, 利用新定义的线性约束, 优化跟踪预测性能指标, 从而有效避免因非线性输入变换而引入的非线性约束;

2) 状态松弛: 设计包含未知状态松弛因子的跟踪预测指标, 通过优化求解预测跟踪序列和松弛因子, 确保输入和状态约束同时存在的情况下优化问题的可解性, 并同时确保闭环系统的稳定性.

总结

本文针对具有输入饱和的非线性混合阶全驱系统, 提出了一种基于级联优化的预测控制方法, 实现了对参考信号的跟踪控制的控制目标. 所设计的双层优化预测级联控制器巧妙地规避了非线性输入变换所引入的复杂非线性约束, 同时通过引入状态松弛因子, 有效保证了优化问题的可解性. 在此基础上, 本文探讨了预测参数与闭环系统稳定性之间的内在关系, 为控制器设计提供了坚实的理论支撑.

未来的研究将进一步聚焦于外界不确定性、模型误差以及环境干扰对系统性能的影响, 致力于开发更具鲁棒性的预测控制策略. 此外, 结合自适应机制, 研究将力求提升控制器在动态未知环境中的自适应能力, 以满足复杂环境下全驱系统的严苛控制需求. 同时, 还将关注控制算法的实时性优化与工程化实现, 推动高效、可靠的预测控制方法在实际应用中的落地, 为工业场景中的复杂控制问题提供创新性解决方案.

作者简介

王秀博博士研究生, 目前研究方向为全驱系统方法、预测控制、飞行器控制和航天器控制;

段广仁中国科学院院士, 国家杰出青年基金获得者, 长江学者特聘教授, 目前研究方向为全驱系统方法、控制系统的参数化设计、鲁棒控制、广义系统、航天器制导与控制.

期刊介绍

《控制理论与应用》(Control Theory & Applications)是经国家科学技术部批准, 教育部主管, 由华南理工大学和中国科学院数学与系统科学研究院联合主办的全国性一级学术刊物, 1984年创刊, 月刊, 国内外公开发行. 《控制理论与应用》是中国科学引文数据库首批统计源期刊之一，中文核心期刊，入选中国精品科技期刊顶尖学术论文F5000项目，中国科协自动化学科领域高质量科技期刊目录以及中国科协百篇优秀科技论文遴选计划，2021年入选广东省高质量科技期刊建设项目，2022-2024年连续获得基金委资助（科技活动专项）。

期刊封面2.jpg 目录2.jpg