博文

【论文推荐】高阶交互下具有环星型结构的分数阶时滞神经网络分岔

已有 150 次阅读 2026-2-12 11:23 |个人分类:论文推荐|系统分类:博客资讯

编辑荐语

本期将给大家分享"高阶交互下具有环星型结构的分数阶时滞神经网络分岔(Bifurcation of fractional-order time-delayed neural network with ring-star structure under higher-order interactions)". 如您对本期相关内容有好的理解与建议, 欢迎评论区留言.

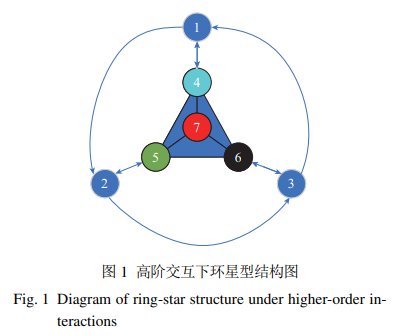
本文聚焦于神经网络动力学研究的前沿领域, 针对传统模型多局限于神经元间二元交互、难以刻画真实大脑中普遍存在的集群式高阶交互的不足, 创新性地提出并研究了一类高阶交互下具有环星型结构的分数阶时滞神经网络模型. 研究首次将高阶交互(以三阶交互模拟神经元群的协同作用)、分数阶导数的全局记忆特性与时滞效应相结合, 构建了更贴近生物神经系统复杂性的理论模型. 通过严谨的数学分析, 论文严格推导了以时滞为分岔参数时系统发生Hopf分岔的临界条件, 揭示了高阶耦合系数、自反馈系数及分数阶阶次等关键参数对网络稳定性与振荡行为产生机制的深刻影响. 数值仿真不仅验证了理论结果的正确性, 更发现高阶耦合对分岔存在非单调的阈值效应, 这一发现对理解神经集群活动的相变机制具有重要启示. 本工作突破了传统二元交互框架, 为探索癫痫发作、记忆编码等神经动力学现象的潜在高阶机制提供了新的理论工具与视角, 对深化神经科学理解及启发新型类脑计算模型具有显著价值.

本研究理论深度与创新性并重, 成功地将高阶相互作用、分数阶微积分和时滞动力学融合于统一的神经网络分析框架中, 所揭示的参数影响机制尤为深刻. 推荐给从事神经动力学、非线性系统、分数阶系统、复杂网络及相关交叉领域的研究人员阅读, 对探索大脑复杂功能背后的数学原理极具启发性.

论文介绍

高阶交互下具有环星型结构的分数阶时滞神经网络分岔

Bifurcation of fractional-order time-delayed neural network with ring-star structure under higher-order interactions

徐士国1, 肖敏1†, 邱建龙2, 杨鑫松3, 黄创霞4

机构: 1. 南京邮电大学自动化学院、人工智能学院; 2. 临沂大学自动化与电气工程学院; 3. 四川大学电子信息学院; 4. 湖南科技学院理学院

引用: 徐士国, 肖敏, 邱建龙, 等. 高阶交互下具有环星型结构的分数阶时滞神经网络分岔. 控制理论与应用, 2026, 43(1): 12 – 21

DOI: 10.7641/CTA.2025.50171

全文链接:

http://jcta.alljournals.ac.cn/cta_cn/ch/reader/view_abstract.aspx?file_no=CCTA250171&flag=1

摘要

目前国内外关于神经网络分岔动力学研究主要集中于神经元间的二元交互, 而神经网络中普遍存在神经元间以群和组的形式发生的高阶交互作用. 但是如今关于高阶交互作用对神经网络动力学的影响研究还不深入. 研究具有高阶交互作用的神经网络可以进一步探索真实神经网络中的高阶属性和动力学演化规律. 为此, 本文提出了一类高阶交互下具有环星型结构的分数阶时滞神经网络模型. 选取时滞作为分岔参数, 给出系统的稳定性和Hopf分岔的充分条件, 揭示高阶耦合系数、自反馈系数和分数阶次对系统动力学的影响机制.

引言

神经网络是大脑信息处理的基本载体. 通过神经元之间的电化学信号传递和突触可塑性机制, 神经网络表现出丰富的动态特性, 包括同步振荡、混沌行为以及分岔现象[1–6]等. 其中, Hopf分岔[7–12]作为一类重要的动态分界点, 能够有效刻画神经活动从稳态到周期振荡的临界转变过程, 为揭示癫痫发作、记忆编码等生理病理机制提供了关键理论工具. 传统神经网络模型大多是基于神经元间的二元交互关系构建[13–15]. 然而, 随着神经科学的深入研究, 科学家发现大脑中不仅包含神经元之间的二元交互, 还包括以群、组的形式发生的高阶交互作用[16]. 如果不清楚神经元群之间复杂的高阶交互机制或者神经网络上复杂的动力学机理, 依然无法揭示大脑的组织结构和运作原理. 为此, 神经网络动力学的研究逐渐从简单的二元交互转向更为复杂的高阶交互作用. 但是目前对于高阶交互作用下神经网络的动力学研究仍处于探索阶段.

高阶交互作用广泛存在于社交网络[17]、生态系统[18]以及化学系统[19]等. 然而, 研究表明人脑从整个大脑网络到局部神经环路具有较强的高阶信息交互(以群或组的形式). 例如, 在神经环路和认知学习方面, 文献[20]揭示了团和洞结构在大脑信息处理中的核心作用. 这些结构不仅促进了局部信息的快速整合, 还通过形成复杂的环状路径支持跨脑区的并行计算, 从而实现了高阶认知功能的高效协调. 在脑疾病诊断方面, 文献[21]通过构建帕金森病患者的高阶功能连接网络拓扑结构, 揭示了患者与健康对照组之间的显著差异. 研究发现, 帕金森病患者的高阶功能网络表现出信息交互的中断和小世界性的减弱, 这表明帕金森病患者的高阶功能网络的平衡被破坏, 导致信息处理效率下降. 因此, 高阶交互分析能够充分捕捉多个神经元之间的相互作用和动态过程. 这类信息交互无法通过神经元之间简单的二元交互, 例如神经元之间的突触连接或人工神经网络中的权重来描述. 综上所述, 高阶交互突破了传统的交互限制, 能够更真实地描述神经集群的同步激活、多神经元协同编码等复杂动力学现象, 精准捕捉真实神经网络的高阶属性和动力学演化规律. 此外, 高阶交互作用可能引入传统神经网络模型未涉及的分岔类型, 进而解释脑疾病发作的突现性相变. 所以高阶交互不仅揭示了神经系统中信息处理的复杂性, 还为理解大脑功能、设计高效的人工智能算法提供了新的视角. 但值得注意的是, 关于高阶交互作用对神经网络分岔动力学的影响机制的研究鲜少提及.

目前神经网络分岔动力学[22]的研究已经取得较多成果, 其中针对星型结构和环状结构的神经网络的分岔动力学方面, 文献[23]首次研究了一类具有3个环和多时滞的高维神经网络的稳定性和Hopf分岔. 文献[24]研究了一个具有多时滞的双环交叉神经网络的分岔动力学. 文献[25]利用带有忆阻器的星型耦合Hindmarsh-Rose神经元模型研究其集体动力学. 文献[26]构建了两个以星型结构进行耦合的Hopfield型神经网络模型并研究其动态行为. 由于整数阶导数具有局部记忆性, 难以精确刻画神经网络系统中广泛存在的动力学行为, 但是分数阶导数可以赋予系统全局记忆性与遗传特性, 因此分数阶模型克服了整数阶模型在描述神经网络系统的不足[27–29]. 在分数阶时滞神经网络研究方面, 文献[30]分别探索了整数阶与分数阶双向联想记忆 (bidirectional associative memory, BAM)神经网络的稳定性和Hopf分岔. 文献[31]研究了具有两种不同时滞的分数阶Cohen-Grossberg神经网络的稳定性和分岔. 文献[32]对多时滞分数阶Hopfield神经网络的Hopf分岔进行了分析. 尽管上述文献都研究了分数阶与时滞对神经网络的影响, 但是都没有引入高阶交互作用, 并探索其对神经网络稳定性与动力学的影响. 也就是说, 目前对于高阶交互作用下的神经网络分岔动力学缺乏研究. 特别是高阶交互作用对神经网络的稳定性和Hopf分岔的影响机制尚未得到有效解答, 这导致了现有理论模型难以准确刻画真实神经网络的动态特性, 制约了类脑计算与神经科学的发展. 为此, 本文通过将高阶交互作用引入具有环星型结构的分数阶时滞神经网络进行研究, 探索高阶交互作用对神经网络稳定性与动力学的影响机制.

本文提出了一类高阶交互下具有环星型结构的分数阶时滞神经网络, 研究了网络的稳定性和 Hopf分岔. 本文的主要贡献如下:

1) 提出了一类高阶交互下具有环星型结构的分数阶时滞神经网络, 构建了环星型三阶交互结构来模拟真实神经网络的架构;

2) 给出了系统的稳定性和Hopf 分岔的充分条件, 严格推导了时滞诱导神经网络Hopf分岔的临界条件;

3) 揭示了高阶耦合系数、自反馈系数和分数阶次对神经网络动力学的影响机制.

本文的其余部分组织如下: 在第2节中, 介绍了预备知识; 在第3节中, 提出了一类高阶交互下具有环星型结构的分数阶时滞神经网络模型; 在第4节中, 分析了系统的平衡点及稳定性, 推导了时滞诱导系统Hopf分岔的临界条件; 在第5节中, 通过数值仿真验证了理论结果的正确性, 揭示了高阶耦合系数、自反馈系数和分数阶次对系统动力学的影响机制; 在第6节中, 得出结论并进行了总结.

640 (1).png

结论

高阶交互作用广泛存在于神经网络中, 但传统的神经网络模型主要集中在二元交互上. 迄今为止, 有关高阶交互作用下的神经网络的动力学研究还很少. 特别是高阶交互作用对神经网络动力学的影响机制更是值得进一步的探索和研究. 为此, 本文研究了一类高阶交互下具有环星型结构的分数阶时滞神经网络分岔. 通过分析特征方程根的分布, 得到系统的稳定性和产生 Hopf 分岔的充分条件. 数值仿真结果表明, 当时滞超过分岔阈值时, 系统在原点发生Hopf分岔, 出现周期性震荡, 并产生极限环. 除此之外, 本文揭示了高阶耦合系数、自反馈系数和分数阶次对系统动力学的影响机制. 其中, 高阶耦合系数对系统分岔阈值的影响存在阈值, 当高阶耦合系数处在阈值范围内, 增大高阶耦合系数会延迟系统的Hopf分岔. 当其超过阈值后, 增加高阶耦合系数会加快系统的Hopf分岔, 增大自反馈系数会延迟系统的Hopf分岔, 增大分数阶次会加快系统的Hopf分岔.

然而, 本文研究的高阶交互下具有环星型结构的分数阶时滞神经网络仍然存在着网络拓扑结构为单层且网络规模小的局限性. 因此, 在未来的研究中将首先研究高阶交互作用下的多层神经网络分岔, 探索高阶交互作用对多层神经网络动力学的影响机制. 此外, 将进一步研究高阶交互作用如何影响大规模神经网络的动力学行为.

作者简介

徐士国硕士研究生, 目前研究方向为高阶神经网络的动力学及控制;

肖敏教授, 目前研究方向为神经网络时空演化、复杂系统突变控制;

邱建龙教授, 目前研究方向为物流系统建模、分析与控制、物流系统设计与开发;

杨鑫松教授, 目前研究方向为群体智能与控制、无人机群空地协同调度;

黄创霞教授, 目前研究方向为微分方程与动力系统、复杂网络与金融风险管理.

期刊介绍

《控制理论与应用》(Control Theory & Applications)是经国家科学技术部批准, 教育部主管, 由华南理工大学和中国科学院数学与系统科学研究院联合主办的全国性一级学术刊物, 1984年创刊, 月刊, 国内外公开发行. 《控制理论与应用》是中国科学引文数据库首批统计源期刊之一，中文核心期刊，入选中国精品科技期刊顶尖学术论文F5000项目，中国科协自动化学科领域高质量科技期刊目录以及中国科协百篇优秀科技论文遴选计划，2021年入选广东省高质量科技期刊建设项目，2022-2024年连续获得基金委资助（科技活动专项）。

期刊封面2.jpg 目录2.jpg