博文
一类带有输入时滞和乘性噪声线性系统的随机最优控制
|
引用本文
王宏霞, 刘祥谦. 一类带有输入时滞和乘性噪声线性系统的随机最优控制. 自动化学报, 2025, 51(11): 2534−2542 doi: 10.16383/j.aas.c240809
Wang Hong-Xia, Liu Xiang-Qian. Stochastic optimal control of a class of linear systems with input delay and multiplicative noise. Acta Automatica Sinica, 2025, 51(11): 2534−2542 doi: 10.16383/j.aas.c240809
http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240809
关键词
最优控制,输入时滞,乘性噪声,随机系统
摘要
研究存在未知系统动力学和输入时滞的乘性噪声系统线性二次最优控制问题. 当系统动力学完全已知时, 可以通过离线求解Riccati-ZXL方程获得最优反馈策略. 而当系统动力学不完全已知时, 离线求解Riccati-ZXL方程不再可行. 为此, 拟设计一种值迭代算法来求解Riccati-ZXL方程, 该算法仅依赖可量测的状态和输入信息, 而不要求完全的系统动力学. 与策略迭代算法不同, 该算法消除了对初始策略稳定性的要求, 具有更强的适应性. 最后, 通过一个例子验证了所提算法的有效性.
文章导读
在实际应用中, 乘性噪声广泛存在于图像处理、金融建模和无线通信等多种系统和场景中. 以往的研究大多假设系统动力学已知[1−3], 而对于部分或全部系统动力学未知的复杂系统, 相关研究较少. 由于系统内在的特性以及外部环境的影响, 精确获取其动力学模型非常困难. 因此, 在缺乏完整系统动力学的情况下如何有效处理乘性噪声引起了广泛关注[4−6]. 一些学者开始探索使用强化学习方法解决相关问题, 并取得了一系列成果[7−11]. 文献[12]提出一种基于Q-学习的无模型算法, 解决了带有乘性噪声的马尔科夫跳跃系统的随机二次最优控制问题, 并提出基于移动平均的方法来减少估计方差. 该算法依赖于扩维空间, 增加了计算复杂度. 文献[13]在策略迭代算法的基础上, 提出一种新颖的Off-policy多轨迹乐观最小二乘策略迭代算法, 可以从在线输入和状态数据中学习随机线性二次调节问题的近似最优解, 而无需精确识别系统矩阵. 然而, 该算法要求每次迭代时的误差有界且很小, 这在实际应用中可能是一个挑战.
值得注意的是, 现有的基于强化学习的算法大多处理仅含乘性噪声或仅有时滞[14−15]的系统, 而对于同时存在乘性噪声和时滞的系统, 基于强化学习的研究则相对较少. 针对具有随机延迟和输入相关噪声的网络化控制系统, 文献[16]通过状态扩维的方法, 提出两种基于Q-学习的算法. 然而, 状态扩维导致所获得的最优状态反馈控制策略与本文寻求的预报反馈控制策略存在显著差异. 前者基于广义Riccati方程, 预报反馈控制则基于Riccati-ZXL方程. 为此, 针对输入时滞的乘性噪声系统, 文献[17]提出一种策略迭代(Policy iteration, PI)算法. 该算法能够直接求解最优预报反馈策略, 而无需完全系统动力学. 然而, PI算法需要有一个镇定的初始策略. 在实际应用中, 找到这样的镇定初始策略往往具有较大挑战, 特别是对于那些具有复杂动态特性和不确定性因素的系统. 这不仅增加了算法实现的难度, 也限制其在实际场景中的广泛应用.
基于上述背景, 有必要提出一种值迭代(Value iteration, VI)算法, 用于解决存在输入时滞和部分系统动力学未知的乘性噪声系统线性二次最优控制问题. 模型参数完全已知时, 由于分离原理不成立, 文献[18]首次提出Riccati-ZXL方程, 证明了具有输入时滞的随机线性二次最优控制问题的解析解(包括充要的可解性条件、最优控制器、最优性能)由Riccati-ZXL方程的解决定. 与标准Riccati方程相比, Riccati-ZXL方程结构更复杂、具有更强的非线性, 求解更困难; 最优控制器具有预报反馈结构而非状态反馈结构. 目前, 除了文献[17]中的 PI算法, 很难找到相关的强化学习研究. 一般情况下, 对于能镇定系统的初始策略, PI算法比VI算法收敛更快. 但在实际应用中, 当模型参数不完全已知时, 很难确定初始策略是否能镇定系统. 这意味着文献[17]中的PI算法无法保证总能有效学习出问题的最优控制策略. 相比之下, VI算法则摆脱了对初始策略镇定性的依赖, 因而具有更广泛的实用性.
本文面向具有输入时滞和部分未知动态的乘性噪声随机线性系统最优控制问题, 提出其最优的预报反馈控制策略. 主要贡献如下: 一方面, 为Riccati-ZXL方程给出一种基于模型的近似迭代解, 并对该迭代解进行收敛性分析; 另一方面, 基于所提出的近似求解理论, 提出一种基于数据的VI算法来解决无完全系统动力学的输入时滞随机系统最优控制问题.
本文其余部分组织如下: 第1节是问题陈述和准备工作; 第2节提出基于模型的离线算法, 并进行收敛性分析; 第3节通过基于模型的离线算法提出基于数据的VI算法; 第4节是数值仿真和结果分析; 第5节是总结.
图1 不同算法的估计误差曲线
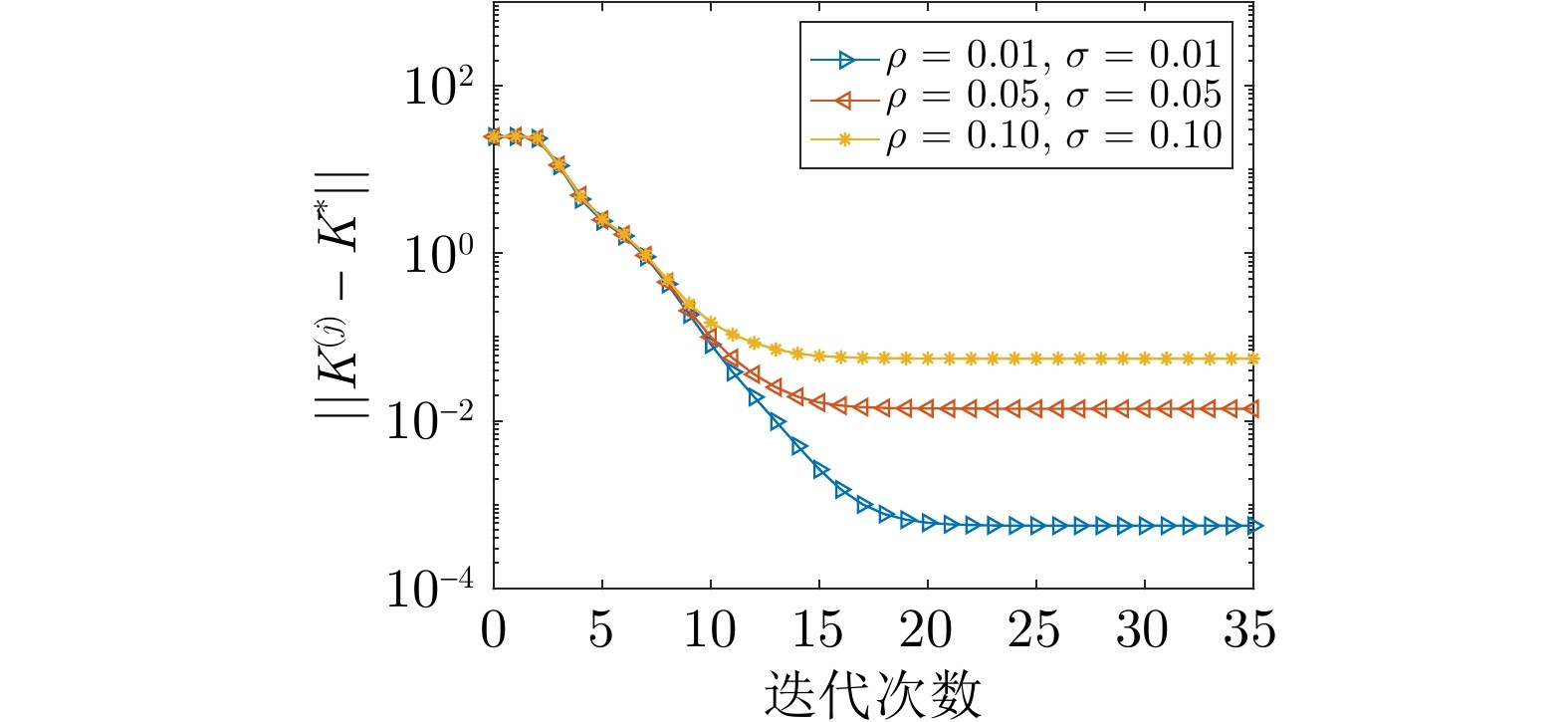
图2 不同干扰强度下的估计误差曲线
图3 不同时滞下的估计误差曲线
本文研究存在未知系统动力学和输入时滞的乘性噪声系统线性二次最优控制问题. 为解决系统动力学不完全已知时难以求解Riccati-ZXL方程问题, 提出一种VI算法. 与PI算法不同, 该算法消除了对初始策略稳定性的要求. 最后, 通过数值仿真验证了所提算法的有效性.
作者简介
王宏霞
山东科技大学电气与自动化工程学院副教授. 主要研究方向为非标准系统的最优控制, 强化学习, 优化算法. 本文通信作者. E-mail: whx1123@126.com
刘祥谦
山东科技大学电气与自动化工程学院硕士研究生. 主要研究方向为强化学习. E-mail: lxq03141018@163.com
https://blog.sciencenet.cn/blog-3291369-1516441.html
上一篇:独立慢特征分析建模方法及其在动态故障检测中的应用
下一篇:基于SF-LPETB的电力信息物理系统虚假数据注入攻击定位检测