引用本文

刘思彤, 高伟男, 姜钟平. 带有输入时滞的非线性系统基于学习的输出反馈控制. 自动化学报, 2025, 51(10): 2293−2301 doi: 10.16383/j.aas.c250101

Liu Si-Tong, Gao Wei-Nan, Jiang Zhong-Ping. Learning-based output-feedback control for nonlinear systems with input time-delay. Acta Automatica Sinica, 2025, 51(10): 2293−2301 doi: 10.16383/j.aas.c250101

http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c250101

关键词

最优控制，输出反馈，时滞，自适应动态规划

摘要

针对具有输入时滞的非线性系统直接自适应最优控制问题, 提出一种新的数据驱动输出反馈控制方法. 该方法通过融合Q学习与值迭代和策略迭代, 在学习过程中无需依赖系统动力学知识. 在系统满足一致可观性的条件下, 提出一种基于输出数据和带有时滞的输入数据的系统状态重构方法, 基于值迭代和策略迭代来学习自适应最优控制策略. 最后, 将该方法应用于范德波尔振荡器这一经典非线性系统的控制, 并通过仿真结果充分验证了该方法的有效性.

文章导读

最优控制问题的核心目标在于设计能够使代价函数最小的最优控制策略. 然而, 现有最优控制研究往往依赖于系统动力学知识[1]. 随着现代工程系统动态愈加复杂, 获取完整的动力学信息变得尤为困难. 为应对这一挑战, 近年来涌现出多种数据驱动方法[2−5], 这些方法通过利用系统的输入输出数据直接进行控制策略的学习和优化, 无需依赖精确的系统模型. 其中无模型自适应控制[6−8]方法计算量小, 适合实时控制, 适用于工业过程控制、机器人控制等场景. 针对非线性系统的最优控制问题, 传统方法常将其转化为求解哈密顿−雅可比−贝尔曼方程, 但直接求解该方程复杂度高、计算量大. 自适应动态规划方法作为一种数据驱动技术, 无需依赖系统模型设计最优控制器, 并且能有效降低计算复杂度. 因此, 该方法受到学者们的广泛关注[9−18]. 与直接求解哈密顿−雅可比−贝尔曼方程的方式不同, 自适应动态规划方法通过迭代的方式来逼近最优控制策略, 从而有效减轻计算负担[19−22].

策略迭代(Policy iteration, PI)和值迭代(Value iteration, VI)是强化学习和动态规划中的两种典型迭代方法, 它们能够在学习过程中同步逼近最优值函数及最优控制策略. 其中, 策略迭代需从可接受的控制策略出发, 且每次迭代生成的策略均保持可接受性[23−24]. 然而, 在模型动态未知的情况下, 获取此类可接受的初始策略往往颇具挑战. 与策略迭代不同, 值迭代无需可接受的初始控制策略, 允许从任意控制策略开始学习, 这一特性使得值迭代在缺乏可接受初始控制策略的无模型场景中更具优势[25−26].

Q学习是一种求解动态规划问题的迭代方法. 具体而言, Q学习通过求解Q函数来寻求最优的值函数和最优的控制策略. 值得注意的是, Q学习不依赖于系统模型信息, 通过利用所有状态和输入信息来更新迭代Q函数, 从而在实际应用中展现出更高的有效性. Q学习可以与策略迭代和值迭代方法相结合, 在完全无系统模型信息的动态系统中探寻最优反馈控制策略[23, 27].

大多数现有非线性系统自适应动态规划方法的研究假设系统全状态信息可测. 然而在许多复杂系统中, 完整测量系统状态信息往往成本高昂或甚至根本不能实现, 在系统动态未知时, 往往不能设计观测器估计系统状态. 因此, 如何利用输入输出信息重构状态是一个理论挑战, 亟需研究基于输出反馈的自适应动态规划方法. 另外, 通讯时滞在实际应用中非常常见, 且时滞如处理不当会严重影响控制性能, 甚至导致系统不稳定, 因此带有时滞的控制问题已成为学者们关注的主要领域[28−31]. 对于线性系统, 系统输入输出与状态之间有相对明确的线性对应关系[32−33]. 但对于系统模型未知、含有输入时滞的非线性系统, 寻找这种关系更为复杂. 为应对以上挑战, 本文针对含有输入时延的非线性离散时间系统, 基于自适应动态规划和非线性最优控制理论, 设计输出反馈自适应最优控制器.

本文的主要贡献如下:

1) 针对一致可观的非线性离散时间仿射系统, 基于系统输入和输出数据, 解决带有时滞的非线性系统状态重构难题.

2) 将Q学习与策略迭代和值迭代相结合, 提出无需系统模型信息的迭代方法, 可以针对带有时滞的非线性系统设计输出反馈自适应最优控制.

3) 将所提出方法应用于范德波尔振荡器, 通过仿真验证了方法的有效性.

本文结构安排如下: 第1节阐述离散时间非线性系统的最优控制问题, 并回顾相关基础知识; 第2节提出状态重构方法, 以及基于模型的值迭代与策略迭代算法; 第3节提出数据驱动的值迭代与策略迭代方法; 第4节将所提方法应用于范德波尔振荡器, 通过仿真验证其有效性; 最后, 第5节对全文进行总结.

图1  时滞系统的输出反馈控制器设计思路

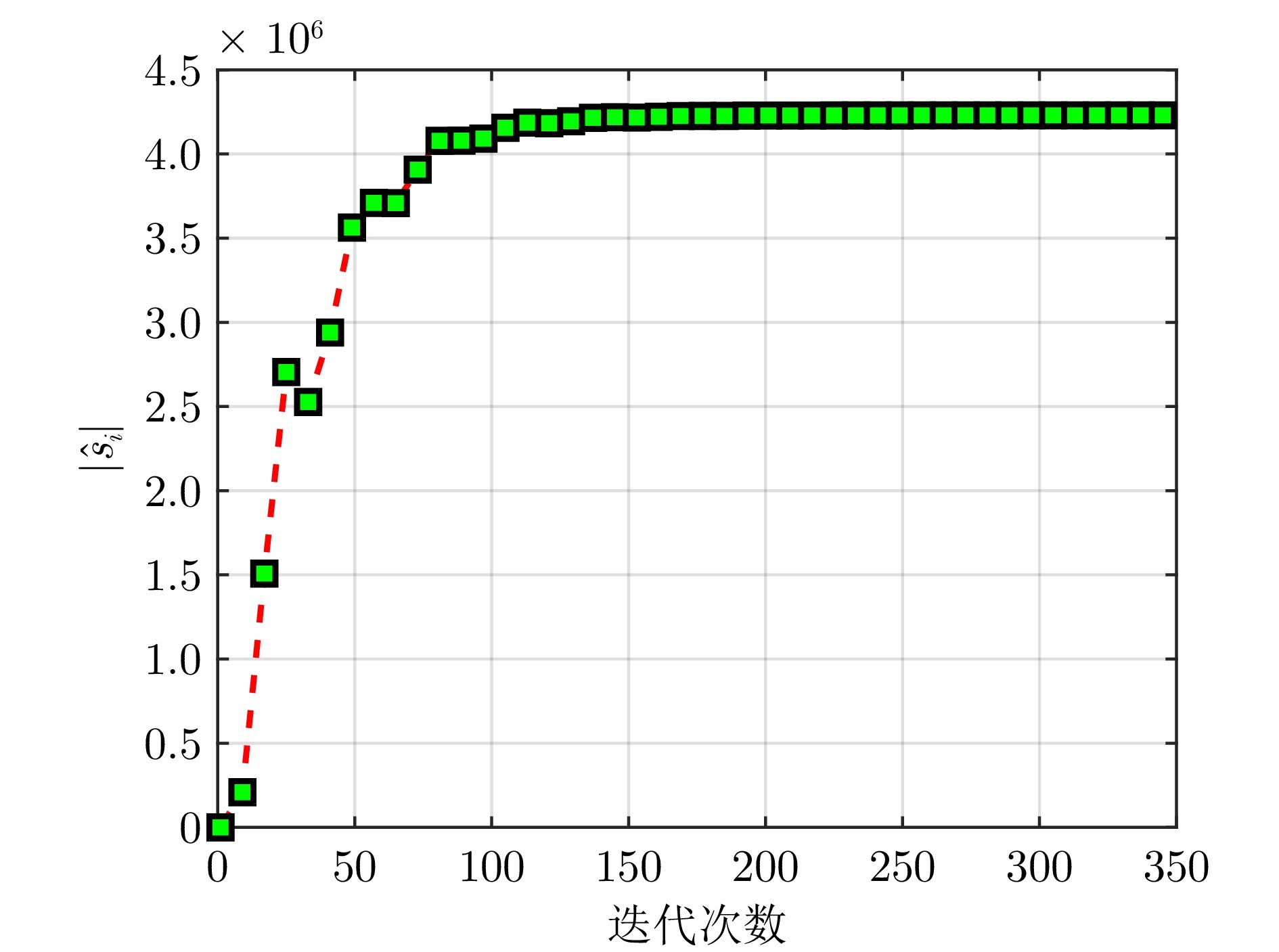
图2  权重范数随迭代的变化情况

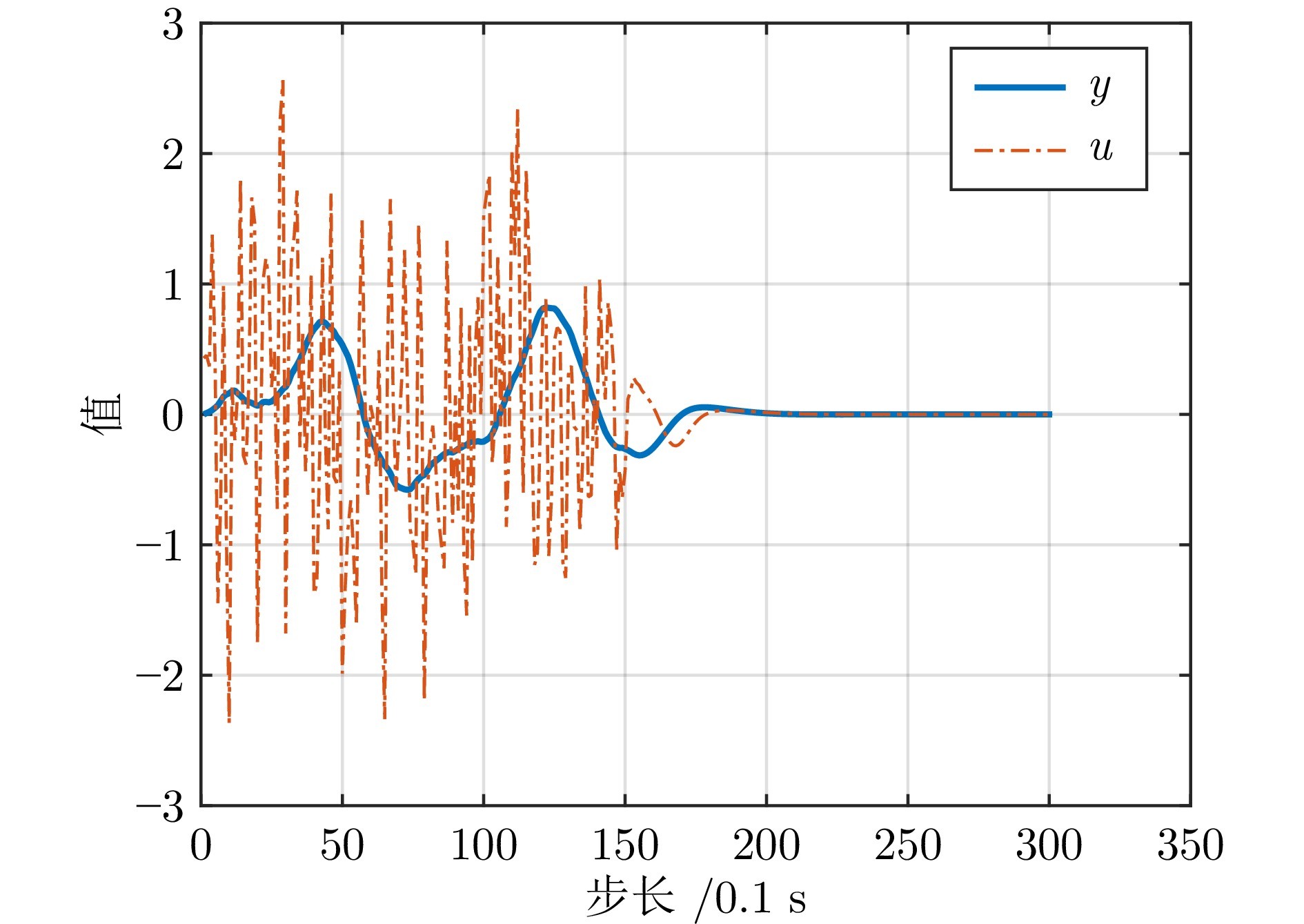
图3  考虑时滞的输出反馈下闭环系统的输入输出轨迹

针对具有输入时滞的非线性系统直接自适应最优控制问题, 本文提出一种新的数据驱动输出反馈控制方法. 通过利用输出和带有时滞的输入数据构建系统状态, 并将其作为反馈, 成功克服了含有输入时滞的输出反馈自适应最优控制策略设计这一挑战. 同时, 将Q学习与两种自适应动态规划方法相结合, 使得算法学习过程中无需依赖系统动力学信息. 仿真结果验证了该方法的有效性.

作者简介

刘思彤

东北大学流程工业综合自动化全国重点实验室硕士研究生. 2023年获得东北大学机械工程专业学士学位. 主要研究方向为自适应动态规划, 输出反馈, 最优控制和强化学习. E-mail: 2370761@stu.neu.edu.cn

高伟男

东北大学流程工业综合自动化全国重点实验室教授. 2017 年获得美国纽约大学博士学位. 主要研究方向为人工智能, 自适应动态规划, 优化控制和输出调节. 本文通信作者. E-mail: gaown@mail.neu.edu.cn

姜钟平

欧洲科学院外籍院士, 美国 纽约大学杰出教授, IEEE Fellow, IFAC Fellow. 1993 年获得法国巴黎高等矿业大学自动控制与数学专业博士学位. 主要研究方向为稳定性理论, 鲁棒/自适应/分布式非线性控制, 鲁棒自适应动态规划, 强化学习及其在信息、机械和生物系统中的应用. E-mail: zjiang@nyu.edu