博文
当相对论文明遇到牛顿力学文明
 精选
精选
||
最近有本 Andy Weir 写的科幻小说《Project Heil Mary》在网上评价很高。跟他写的《The Martian》一样,也是个孤胆英雄流落在外星球试图重返家园的故事。但新书里的主人公的任务更为艰巨,经历更为神奇。根据维基百科介绍,其中关键情节是,孤胆英雄被困于几光年外的一个恒星轨道上,遇到了另一个恒星来的一艘外星飞船,船上只有一个外星人。那艘飞船所在的文明尚未发现狭义相对论,也不懂高能物理,动力学水平停留在牛顿力学的层次。外星人按照10光年的往返旅程准备了燃料,结果到达后发现还有大量的剩余燃料。地球人与外星人结成了莫逆之交,分享各自的知识与发现。这是一个温馨的故事。
外星人述说道,他们准备了10光年旅程需要的燃料。飞船一路加速,但到后来速度怎么也上不去了,查发动机运行状况一切正常;另外一件奇怪的事就是,目标距离缩短了很多;于是他开始让发动机反方向喷射进行减速,结果发现目标距离又变远了,不得不又加速。如此反反复复,才跌跌撞撞地到达目的地。对此,地球人费了很大劲才教会外星人相对论空时的概念。
小说里对外星人多算了燃料的解释是,因为外星飞船加速到接近光速,在相对论尺缩效应下,其实际单向旅程缩短了。小说里当然没有详细的计算,也没有就考虑各种相对论动力学的效应。现在问题来了,用相对论计算真的比按牛顿力学算需要更少的燃料吗?下面我们看看根据不同的理论要把一定的质量加速到某个速度需要多少燃料。(我发现直接在计算机上进行代数计算是最高效的,因为写得更紧密更清楚,而且修改错误更容易。下面基本一步不漏。)
我们知道,用牛顿力学计算火箭速度,结果中不是简单的质量比,而是火箭前后质量比的对数,这是因为在火箭加速必须也得把携带的燃料一起加速,而随着火箭喷射,燃料减少,火箭总质量也在减少。牛顿力学计算如下。设火箭相对地球当前速度为 v,质量为 m, 喷射燃料 \delta m, 燃料相对于火箭的速度为 V,根据动量守恒,我们可以算出火箭速度的变化 dv。最方便的参照系是以随火箭以速度 v 运动的惯性参照系,在这个参照系里,火箭出于瞬间禁止状态,动量为零,然后喷射燃料获得 dv 加速。动量守恒方程为:
$\delta m \ V + (m- \delta m)\ dv =0$
忽略二阶小量 $ \delta m\ dv $, 我们有
$\delta m \ V + m\ dv =0$
$dv = - V \delta m/m$
在伽利略变换下,火箭相对于地球的速度是将运动参照系速度 v 与 dv 简单相加。因此,我们可以将上面 dv 积分而得出相对于地面的速度增量:
$\Delta v = -V \ln (m_i/m_f)$
其中 m_i, m_f 分别是火箭起始质量与结束质量。消耗的燃料质量 M 为两者之差。
$m_i = m_f + M = m_f \ e^{-\Delta v/V} \\ M = m_f \ (e^{-\Delta v/V} -1)$
飞船的航程设计如下,火箭喷射加速,飞船从零速开始加速到速度 U,这个加速在较短的时间内完成;然后以这个速度巡航大部分时间;快到目的星球时,再反向喷射从速度 U 减速到零。则依照牛顿力学,两段加起来需要的燃料质量是:
$M_1 = m_f \ (e^{U/V} -1)\\ M_2 = (m_f +M_1) \ (e^{U/V} -1) \\ M = M_1 + M_2 = m_f (e^{U/V}-1) + m_f [1+ (e^{U/V}-1)] (e^{U/V}-1)\\ M=m_f\ (e^{2U/V}-1)$
在狭义相对论理论下计算有两处与牛顿力学不同,我们得考虑动量的相对论修正与相对论速度的叠加。在飞船瞬时静止的参照系计算速度增量,换成地面参照系需要使用速度叠加公式,鉴于此,我们直接在地面参照系进行动量计算。
在飞船参照系,以速度 V喷出的静质量为 $\delta m$ 的动量为 $\delta p = \delta m\ V/\sqrt{1 - V^2}$, 能量为 $\delta E = \delta m/\sqrt{1 - V^2}$ (c=1)。令 $\gamma_0 = 1/\sqrt{1-V^2}$, 在地面参照系列出动量守恒方程,也就是喷射 $\delta m$ 前火箭 (质量m,速度 v )的动量等于喷射后火箭与燃料的动量和。下面我们换到地面参照系。
在地面参照系,喷射前火箭的动量是: $p = m v /\sqrt{1-v^2}$;
喷射出的燃料动量是 (套用洛伦茨变换 x->p, t->E): $\delta p = 1/\sqrt{1-v^2}\ (\gamma_0 \delta m \ V + v\ \delta E) = \gamma_0 \ \delta m (v+V)/\sqrt{1-v^2}$ ;
喷射后火箭的动量是: $p^\prime = ( m -\gamma_0\ \delta m)\ (v+dv) /\sqrt{1-(v+dv)^2}$ 。注意火箭静质量减少为 $\gamma_0\ \delta m$ 。
动量守恒方程为 :$\delta p + p^\prime = p$
也就是:
$\gamma_0 \ \delta m (v+V)/\sqrt{1-v^2} + ( m -\gamma_0\ \delta m) (v+dv)/\sqrt{1-(v+dv)^2} = m v /\sqrt{1-v^2} $
利用近似:$\sqrt{1-(v+dv)^2} \approx \sqrt {1-v^2 -2v \ dv} \approx \sqrt{1-v^2}\ [1-v \ dv /(1-v^2)]$
动量方程为:
$\gamma_0 \ \delta m (v+V)/\sqrt{1-v^2} + ( m - \gamma_0 \ \delta m) (v+dv) [1+v \ dv /(1-v^2)]/\sqrt{1-v^2} = m v /\sqrt{1-v^2}$
也就是:
$\gamma_0 \ \delta m (v+V)+ ( m -\gamma_0 \ \delta m) (v+dv) [1+v \ dv /(1-v^2)] = m v $
忽略二阶及以上项:
$ ( m - \gamma_0 \ \delta m) (v+dv) [1+v \ dv /(1-v^2)] \\ = (mv +m\ dv - v \ \gamma_0 \ \delta m) [1+v \ dv /(1-v^2)]\\ =mv + m \ dv - v \ \gamma_0 \ \delta m + mv^2 \ dv /(1-v^2)$
简化动量方程为:
$ \gamma_0 \ \delta m\ (v+V) + m \ dv - v \ \gamma_0 \delta m + mv^2 \ dv /(1-v^2) =0 \\ \gamma_0 \ V \ \delta m+ m \ dv /(1-v^2) =0$
继续,火箭质量增量为 [ix]dm = -\gamma_0\ \delta m [/ix]:
$d m/m = \frac{dv}{V (1-v^2)}$
$V \ dm/m = \frac{dv}{ 1-v^2 } = \frac{1}{2}(\frac{dv}{1-v} + \frac{dv}{1+v})$
两边积分:
$V \ln m = \frac{1}{2}(\ln (1+v) - \ln (1-v))= \frac{1}{2} \ln\frac{1+v}{1-v} +C $
代入初始条件 (v=v_i, m=m_i) , 得出 $C = V \ln m_i - \frac{1}{2} \ln\frac{1+v_i}{1-v_i}$
因此:
$V \ln m/m_i = \frac{1}{2}(\ln (1+v) - \ln (1-v))= \frac{1}{2} \ln\frac{1+v}{1-v} - \frac{1}{2} \ln\frac{1+v_i}{1-v_i} $
$\frac{m_f}{m_f+M} =\left[\frac{(1-v_i)\ (1+v)}{(1+v_i) \ (1-v)}\right]^{\frac{1}{2\ V}}$
得出从 0 加速到 U 需要的燃料质量为:
$M = m_f \left[ (\frac{1-U}{1+U})^{\frac{1}{2 V}} -1\right]$
类似的,从0加速到U, 然后再从 U 减速速到 0 需要的总燃料质量用火箭最终质量 m_f 表达为
$M = m_f \left[ (\frac{1-U}{1+U})^{\frac{1}{V}} -1\right]$
注意上面公式中 V 负的。在下面重新定义 V = |V|。
为了与牛顿力学的结果对比,我们计算相对论结果的需要的燃料质量与牛顿力学需要的燃料质量的比:
$R_{n/r}= \left[ (\frac{1+U}{1-U})^{\frac{1}{V}} -1\right] /(e^{2U/V}-1)$
对于大于0的速度U,这个比例 R 总是大于1 的。 对 V=1/10, 1/5, 1/3,1/2, 2/3, 1 绘图结果如下 (如果我没算错):
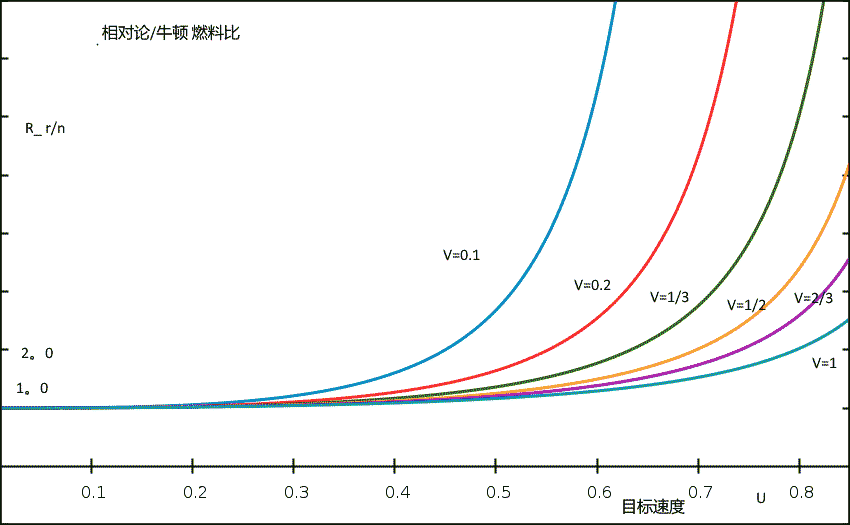
由上图直观可见,相对论计算需要的燃料总是超过牛顿力学计算所需要的燃料。证明这个比例 R 总是大于 1的方法之一是对分子、分母中的指数部分取对数然后比较其大小。 然后证明 当 U < 1 时, $\ln (1+U) - \ln (1-U) \ge 2 U $ 。 两边都是单调增函数,v=0 时左右 都为0,右边导数为2,而左边的导数为 1/(1-U) + 1/(1-U) = 2/(1-v^2) >= 2。
即使喷射速度为光速,要达到 0.7c, 相对论理论给出的燃料需求是非相对论理论的 ((1+0.7)/(1-0.7)-1) / (e^1.4 -1) ~ 1.53 倍。
上面的计算表明,《Project Heil Mary》里的分析是错误的(注一),非相对论文明会大幅少算所需要的燃料。非相对论文明的外星人不会多带燃料,而是会少带燃料。当他抵达目的地后,会发现以原定速度回去已经燃料不够了。
但外星人也许不会立刻绝望。根据相对论,高速飞行的飞船上的人看到两个星球上距离缩短,因而飞船上船员的旅行时间也会缩短。如果飞船以 0.7 倍光速运行,那么原来 10 光年的距离在宇航员看来成了 10 *sqrt(1-0.7*0.7) ~ 7.1 光年,原来宇航员以为需要 10/0.7 ~ 14.3 年才能到,结果 7.1/0.7 ~ 10.1 年就到了。如果他原来准备了 14.3 年的食物,那么抵达时发现多出 4 年的美味。燃料虽然不够,食物还是有剩余。回程因为燃料不够就只能降低速度慢点走了,好在食物还相当充足,可以慢慢想办法。
不过,等他回去时会发现,他母亲星球上的人们比他多老去了至少 4.2 年。
注一:非相对论文明不知道光速是极限,因此可能设计飞行速度是超光速的,不过小说中没有提到这一点,我们也就不考虑牛顿力学下超光速飞行的燃料需求了。
https://blog.sciencenet.cn/blog-684007-1304964.html
上一篇:从“姓”字论证中国五千年文明
下一篇:金字塔的大石块是怎么搬上去的