博文
充液系统动力学(三):椭球充液腔与粘性影响
 精选
精选
|
1. 椭球腔的等效刚体
前文 “充液系统动力学(二)” 中叙述了全充无旋理想流体的 Rhukovsky 等效刚体理论,本文以椭球腔为例作具体计算 (图 1)。以椭球腔的中心 O 为原点,设 (O-x1x2x3) 为椭球腔的主轴坐标系,aj (j = 1,2,3) 为椭球半轴,腔壁 Σ 的曲面方程为
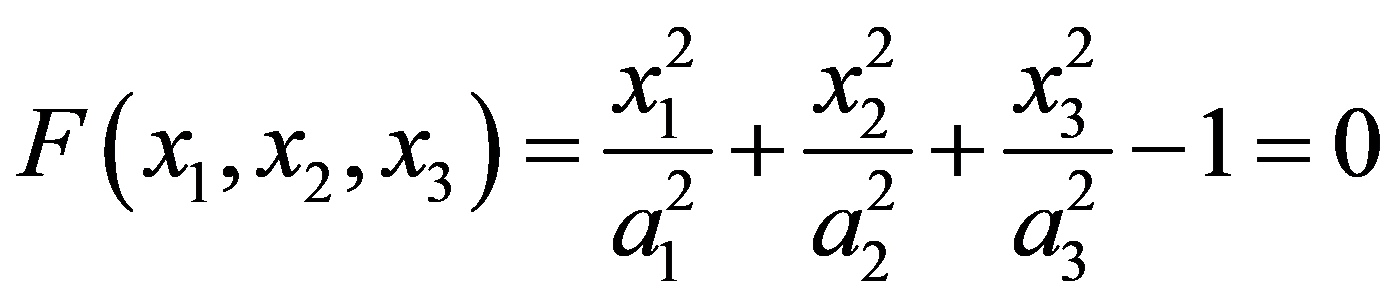 (1)
(1)
图1 椭球形充液腔
利用曲面函数 (1) 对坐标的偏导数,计算 Σ 曲面上任意 P 点处的法线相对 (O-x1x2x3) 各轴的方向余弦 nj (j = 1,2,3),得到
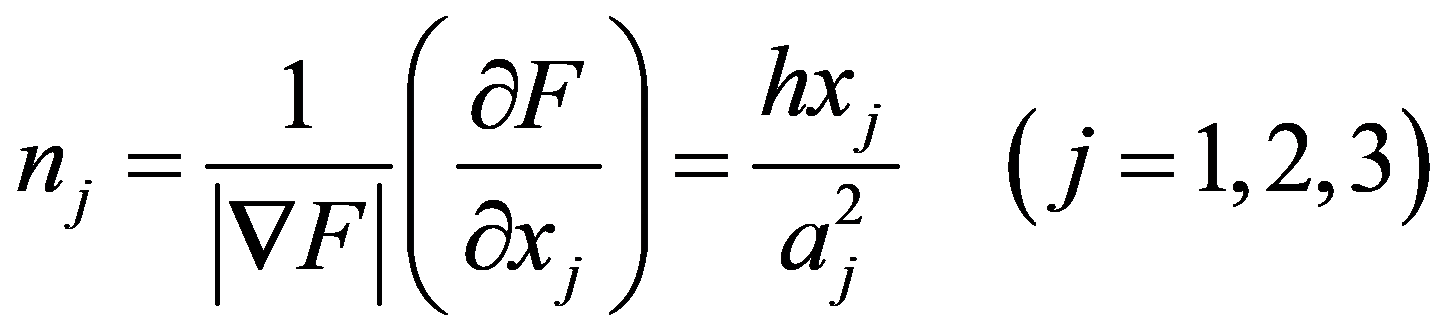 (2)
(2)
令上式两边乘以 xj 后求和,利用式 (1) 导出
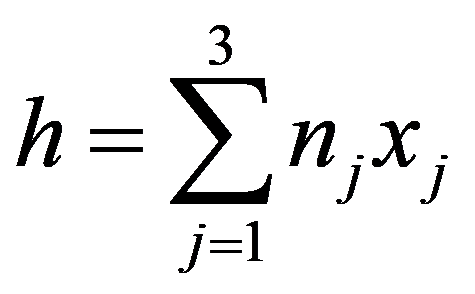 (3)
(3)
从上式和图 1 可看出,h 的几何意义为 O 点至 P 点处切平面的距离。势函数 ψ 在 Σ 处的边界条件为 ∂ψ/∂n = r×n,利用 r = x1i+ x2j+ x3k 及式 (2),此边界条件化作
 (4)
(4)
为能满足此边界条件,将势函数 ψ1, ψ2, ψ3 设计为
![]() (5)
(5)
利用边界条件 (4) 解出常数 Cj (j = 1,2,3),使势函数确定为
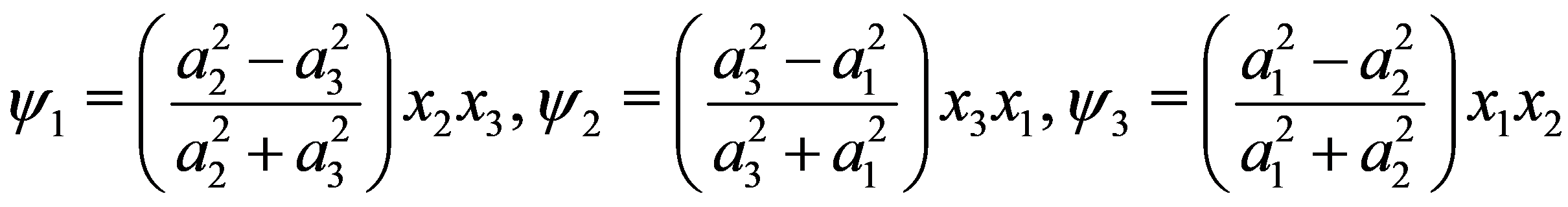 (6)
(6)
将式 (6) 代入等效刚体惯性张量的计算公式:
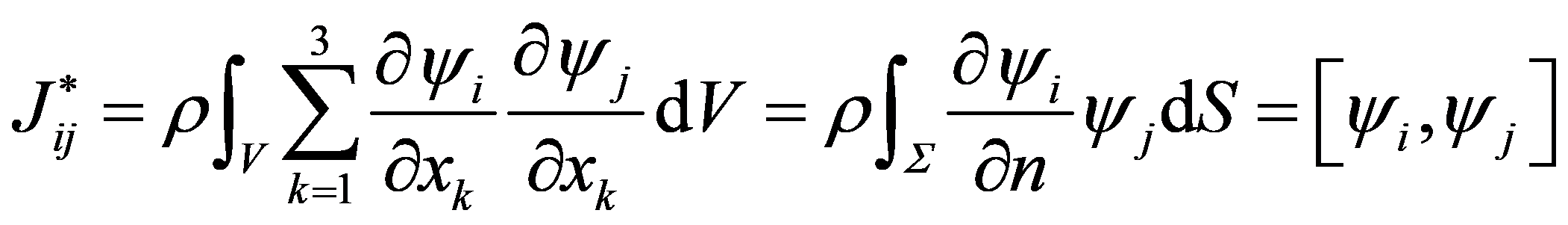 (7)
(7)
积分得到
 (8)
(8)
其中 m = (4π/3)ρa1a2a3 为全充满于椭球腔内的液体质量。
作为特例,如椭球腔为相对 x3 轴对称的旋转椭球。令 a1 = a2,λ = a3/ a1 为椭球的半轴比,得到
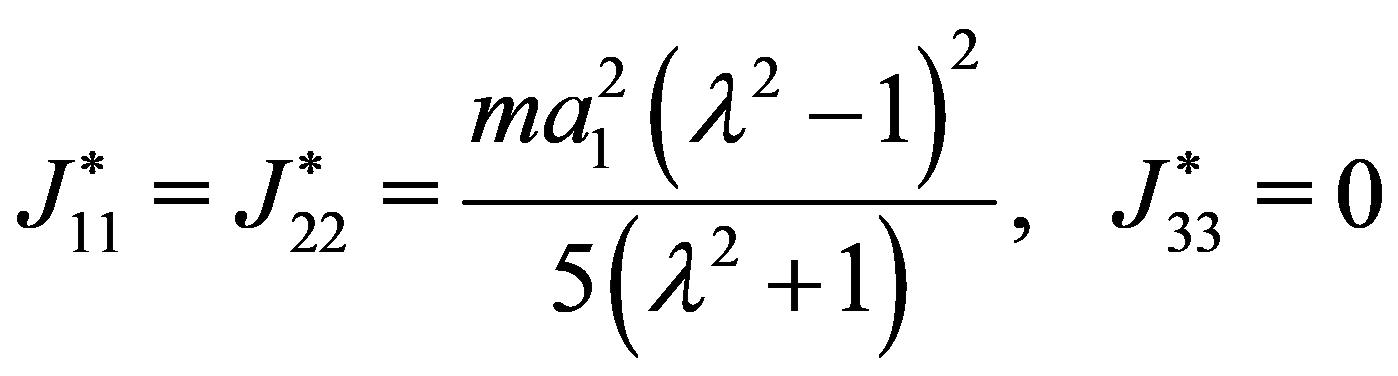 (9)
(9)
等效刚体缩为沿对称轴分布的直线。如为球形腔,令 a1 = a2 = a3,得到
![]() (10)
(10)
即球腔的等效刚体缩为一个质点。上述结论不难从物理观点作出解释:由于理想流体不存在黏性摩擦力,当主刚体绕腔体的对称轴旋转时,腔壁的法向约束力均指向对称轴,不可能带动原来静止的液体绕对称轴旋转,等效刚体绕对称轴的惯性矩必等于零。球腔的腔壁的法向约束力均指向球心,刚体绕任何轴旋转均不可能带动腔内液体的运动。将盛满水的脸盆缓慢转动,观察盆内的水能否保持平衡就是最简单的实验。
2. 流体粘性与边界层理论
在实践中观察,上述球腔内流体的运动并非完全不受刚体运动的影响。原因是任何流体不可能绝对无粘性。对理想流体的分析结论不可能完全符合实际情况。要使理论分析更符合实际情况,必须考虑粘性的作用。
考虑液体粘性的 Navier-Stokes 方程的数学求解非常困难。为此必须想出更容易处理的方法。德国力学大师普朗特 (Prandtl,L.) 提出了一个很重要的概念,即边界层理论(图 2)。这个理论认为,对于粘性较小的一般情况,粘性对流体运动的影响仅局限在与腔壁接触的薄边界层以内。边界层以外流体的运动仍可视为理想流体。因此 Rhukovsky 等效刚体理论仍可利用,但仅限于边界层以外区域内的流体。
图2 普朗特(Prandtl,L., 1875-1953)
依据边界层理论,边界层的厚度 δ 与运动粘性系数 ν = μ/ρ 的平方根成比例。μ, ρ 分别为流体的粘性系数和密度(具体分析可参阅文末的附录)。以一元流动的最简单情形为例,设平板朝 x 轴方向以速度 v 运动,流体沿 x 轴的流速为 u。平板对流体作用的粘性切应力 τ 沿 v -u 方向,与边界层内流速变化的梯度 (v - u)/δ 成正比 (图 3):
 (11)
(11)
图3 边界层内的流速梯度
要分析此粘性切应力如何影响流体的运动,就不能将腔内流体视为理想流体。若为离散化起见,将腔内的流体团视为不变形的刚体,则由于腔壁的限制,只有球形腔内的流体是唯一不受腔壁约束的特例。将球腔内的流体 “固化” 成刚性球体后,其在腔内的转动不受腔壁的约束。如忽略边界层粘性力的存在,球形流体团在腔内的旋转就与主刚体的运动完全解耦,不能正确反映充液刚体的实际情况。要反映主刚体与腔内流体之间的耦合作用,必须考虑边界层的粘性力对刚体球运动的影响。
以半径为 R 的球腔中心 O 为原点,建立已固化为刚体的流体团坐标系 (O-xyz),球面上任意点 P 相对 O 的矢径为 R,P 点的位置以球坐标 (R,θ,ϕ)表示(图 4),则在 P 点处的微元面积 dσ = Rsinθdθdϕ 內腔壁作用的粘性切向力为 τdσ,对 O 点构成粘性摩擦力矩 Md :
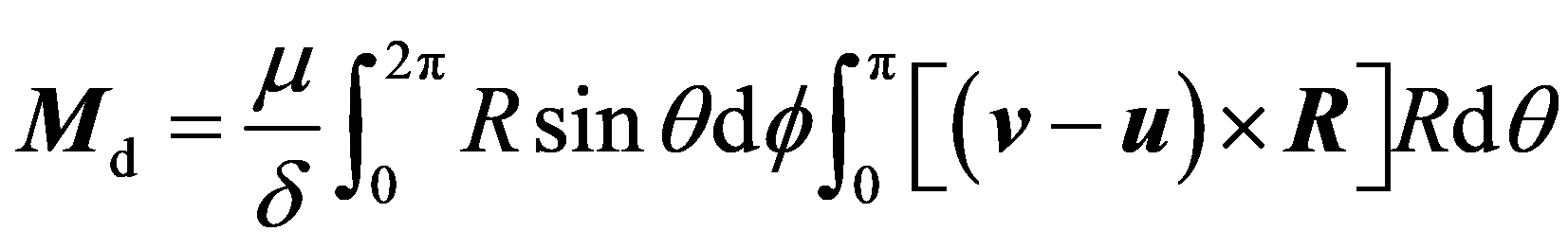 (12)
(12)
图4 流体团的球坐标
于是充液腔刚体的运动被离散化为主刚体和刚体球组成的双刚体系统,刚体之间藉粘性摩擦力矩 Md 维持联系。可利用离散系统的传统方法建模和求解。
以上分析仅限于球形腔特例。关于一般形状腔内的有旋流动将在另文中叙述。
附录:关于边界层的厚度和流速分布的分析
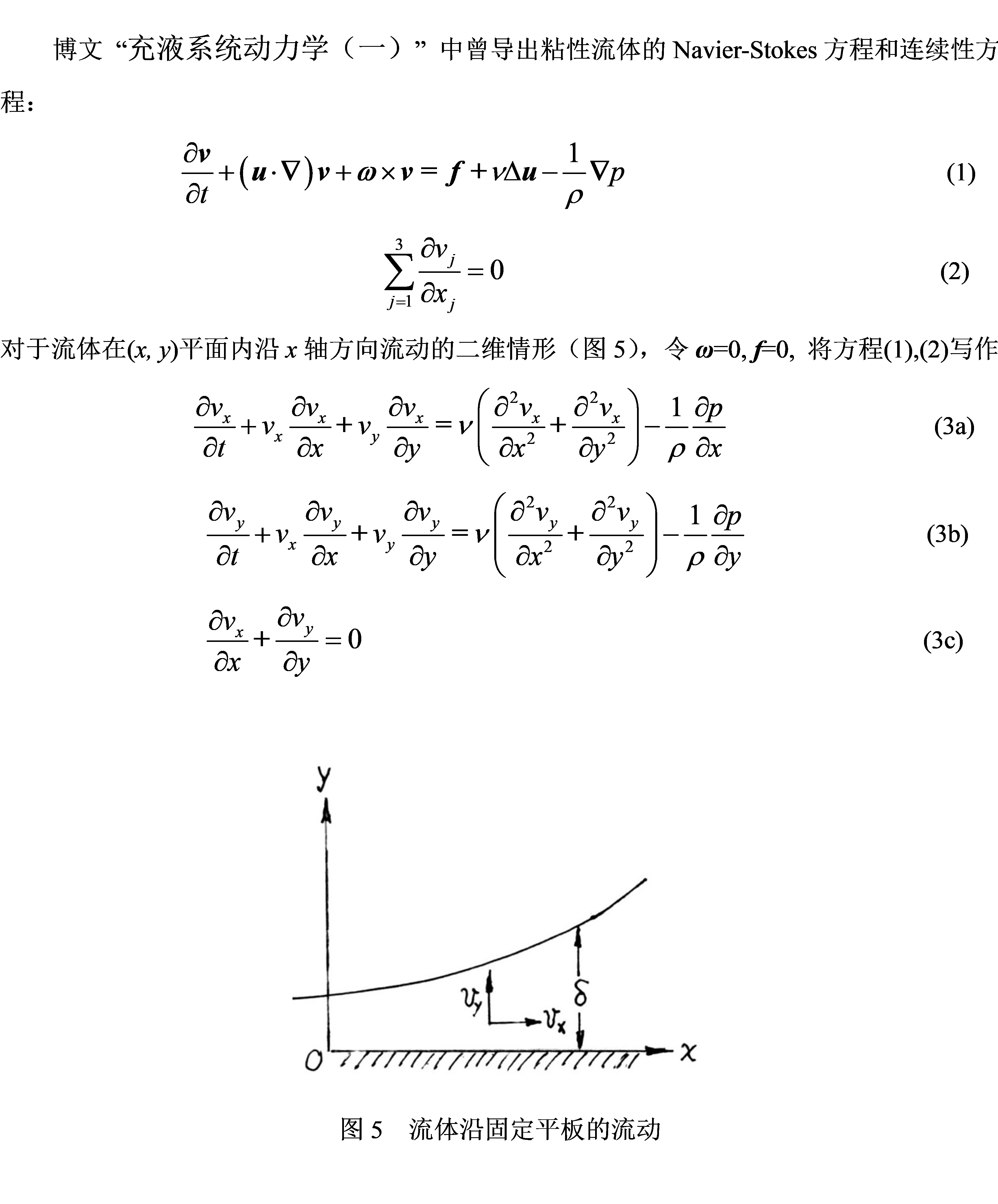

图6 边界层内的流速变化
(改写自:王照林,刘延柱. 充液系统动力学. 第2章. 北京:科学出版社,2002
刘延柱. 陀螺力学(第二版),第10章. 北京:科学出版社,2009)
https://blog.sciencenet.cn/blog-3452605-1313224.html
上一篇:充液系统动力学(二):茹可夫斯基等效刚体
下一篇:充液系统动力学(四):均匀涡旋运动