【按：超声速流动混合是航天航空中一项很重要的研究，在超燃冲压/冲压喷气发动机中，如何精确及有效的测量可压缩混合层的厚度及增长率，至今没有解决，佘振苏团队基于结构系综理论(structure ensemble theory)和测量的PIV流动显示实验结果, 发展了一种直接测量可压缩混合层厚度及增长率的方法，灰度系综平均法(gray-level ensemble average method), 请大家讨论，批评！】

可压缩混合层是航空航天推进装置内部的典型流动之一. 半个世纪以来, 人类对航空航天技术发展的广泛需求极大推动了可压缩混合层的相关研究. 在超声速／高超声速流动中, 混合气体呈现出可压缩性, 会造成密度、温度、压力的脉动并伴随压缩波和激波等流动现象的发生. 由压缩性导致的速度和密度变化会直接影响混合效率, 往往造成可压缩混合层混合效率的显著下降.

混合层的混合效率通常由厚度增长率来定量描述. 由于人们对厚度的多种定义方式缺乏深刻理解, 而测量分析手段又不尽相同, 导致目前诸多实验结果难以吻合. 北京大学湍流与复杂系统国家重点实验室佘振苏团队在可压缩混合层研究中引进了结构系综理论(SED), 用于定量分析流动显示实验结果, 对混合层厚度非线性增长特征提供了有力的实验证据, 为以往研究结果的差异提供了物理解释.

该项研究成果发表于《中国科学：物理, 力学和天文学(英文版)》2014年第57卷第5期上, 由佘振苏、陈军、王铁进等共同合作完成.

高马赫数情况下流体混合研究成果被广泛应用于为航天器提供动力的超声速/亚声速冲压发动机设计. 缺乏对可压缩湍流的认识是阻碍完美工程设计的瓶颈. 研究发现, 压缩性趋向于将湍流流动稳定化并降低混合层增长率. 其负面作用十分显著—相关的化学反应被推迟、混合长度被动延长. 这对降低发动机重量和尺寸等工程设计需求提出了严峻挑战.

以往研究表明, 可压缩混合层流动通常经历三个阶段：(1)由平行流动转化为Brown-Roshko涡; (2)形成二次涡结构和拟序结构的级串; (3)充分发展的剪切湍流. 如改变流动条件, 还会出现更为复杂的流动现象. 虽然大量研究成果丰富了人们对于可压缩剪切流动的认识, 但如何分析海量实验和计算数据以及如何客观、可靠地提取物理参量仍是当前空气动力学领域研究的重要课题.

佘振苏团队提出了称为“结构系综理论”(SED)的新的理论框架, 采用一系列相关统计参量(序函数)来定量描述复杂系统的系综物理意义. 在本项研究中, 对两种对流马赫数—M_c=0.11 (M₁=2.0, M₂=1.5) 和 0.47 (M₁=2.0, M₂=0.6)—开展实验研究, 获得了流场的激光片光米氏散射(PLMS)图像. PLMS技术将雾化乙醇液滴注入高速流中形成30微米以下的示踪粒子, 通过激光片光照射获取表示粒子浓度分布的灰度场, 从而显示出流场内部流动结构. 实验结果清晰显示了Kelvin-Helmholtz不稳定性造成的流动转捩结构和Brown-Roshko (BR)涡. 在M_c=0.11的情况下, 观测到了爆发(eruption)和平移(shifting)现象. 在M_c=0.47情况下, 流动三维化更为突出. 实验成功再现了超声速剪切流动的重要特征.

本项研究基于SED框架重点对PLMS跨流向灰度分布系综进行分析. PLMS灰度图像显示跨流向灰度分布具有良好的自相似性, 研究据此提出了灰度系综平均方法(GLEAM). 该方法通过相似结构系综统计, 准确提取沿流向变化的混合层厚度和增长率, 具体结果如图1所示. 据此分析发现, 厚度尺度的非线性增长普遍存在于湍流混合层的各发展阶段.

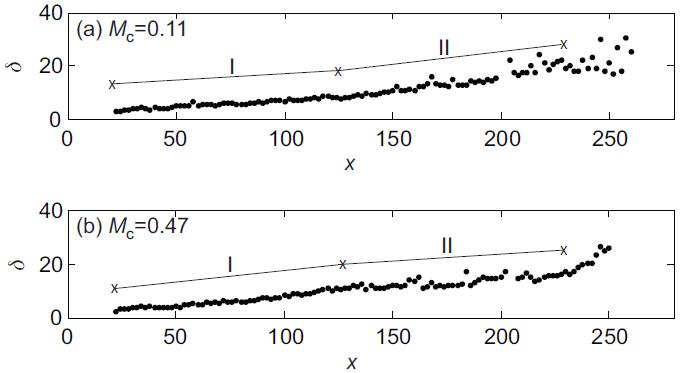
图1 可压缩混合层厚度和增长率. 实线表示用于计算各发展阶段厚度的线性拟合结果. 阶段I和II分别表示混合层的发展初期和发展后期两个阶段.

采用由同样密度和速度条件下的不可压混合层增长率对可压缩条件的增长率进行归一化计算便获得归一化增长率. 该参数可对不同条件下的混合效率进行客观比较. 归一化增长率分析发现了如下四种情况：对于M_c=0.11, 阶段I为Kelvin-Helmholtz不稳定性导致的拟序结构产生阶段; 阶段II为充分发展阶段, 涡结构拉伸和变形逐渐显著; 对于M_c=0.47, 阶段I充满小结构, 无明显拟序结构出现; 但在阶段II, 大尺度结构运动明显增强, 该阶段增长率反而对比上游有所下降. 由此可见, 在两种对流马赫数情况下, 低增长率往往出现在大尺度涡结构发展充分的区域.

通过对上游喷管边壁边界层厚度与混合层增长率的比较分析, 发现来流条件对下游混合层的发展也有影响, 因此压缩性效应和来流条件均是影响混合层增长的关键因素. 该研究证实了GLEAM方法可准确测量可压缩混合层厚度和厚度增长率, 同时该方法可推广应用于其他可压缩剪切流动的结构系综研究.

On quantification of the growth of compressible mixing layer

CML has been a research topic for more than five decades, due to its wide applications in propulsion design. Mixing in CML is controlled by the compressibility effects ofvelocity and density variations over the mixing layer, and quantified by the growth rate of CML. However, the lack of understanding of various definitions ofmixing thicknesses has yielded scatter in analyzing experimental data. Prof. SHE ZhenSu and his colleagues at the State Key Laboratory for Turbulence and Complex Systems, Peking University investigated the growth of compressible mixing layer by introducing an SED theory. Applying the method to experimental data, they provided a solid evidence for the nonlinear growth in CML. Their work, entitled “Experimental evidence for non-linear growth in compressible mixing layer,” was published in SCIENCE CHINA Physics, Mechanics & Astronomy. 2014, Vol 57(5).

The study of fluid mixing enhancement at high Mach numbers is of critical value to engineering applications such as the design of scramjet/ramjet engines of high-speed vehicles. The impediment to a perfect design is the lack of understanding of compressible turbulence. One found that an increase of compressibility tends to stabilize turbulent flows and reduce the growth rate of CML. Passive effects of compressibility are obvious – chemical reactions are delayed, and the mixing length has to be extended. Reducing extra weight and size of the engine is always a challenge for engine design.

In order to understand the underlying physics of CML and find effective control strategies to enhance the mixing in supersonic flow, researchers take the planar compressible mixing layer as a simplified and conceptualized model in their experimental or numerical studies. It produces the mixing layer by introducing two parallel super-/supersonic or super-/subsonic streams. This experimental configuration allows for a clear visualization and detailed measurement.

Previous studies of CML have shown that the flow undergoes at least three stages while convecting downstream —(a) formation of Brown-Roshko vortices (a type of coherent structures) being transitioned from the parallel flow, (b) formation of secondary vortices and the cascade of the coherent vortices, and (c) the well-developed turbulent shear flow, though other structures have been observed when applying different conditions. A wealth of results have enriched our knowledge of the compressible shear flows, but how to analyze the massive experimental and numerical data, and to objectively and reliably deduce physical measures remains an open question.

She’s team has presented a new framework called SED, which aims at using a set of relevant statistical quantities (called order functions) for a quantitative description of the ensemble means. In this work, the SED approach yields a set of gray-level ensemble quantities for a turbulent compressible mixing layer, when analyzing experimentalimages of the planar laser Mie scattering (PLMS) technique, at two convective Mach numbers, M_c=0.11 (M₁=2.0, M₂=1.5) and 0.47 (M₁=2.0, M₂=0.6), which were obtained by seeding ethanol into the low- or the high-speed stream by an atomizing spray nozzle, with ethanol droplets less than 30μm in diameter. The images show clearly a set of transitional coherent structures (CS) ofa Brown-Roshko(BR) type or by a Kelvin-Helmholtz instability. The eruption and shifting of the mixing layer were observed at M_c = 0.11.Three-dimensionality of the flow is visible at M_c = 0.47. Hence, a CML exhibits typical features of supersonic shear flow.

The ensemble of the transverse PLMS gray-level was analyzed in the SED framework. The gray-level images are shown to exhibit a similarity, which is the base for developing theGLEAM method. The GLEAM is able to determine the thickness and growth rate of CML as a function of the streamwise location, as illustrated in Figure 1. Nonlinear growth of the mixing layer is shown to exist in the development of this CML.

Figure 1.  Thickness and growth rate of the CML. Lines indicate the linear fit of the thickness to obtain the growth rate for each stage of mixing.

The growth rate normalized by the incompressible mixing layer at the same density and velocity ratiowas used to compare the results at different flow conditions. Four situations are identified: for M_c = 0.11, Stage I corresponds to the situation with coherent structures generated with the Kelvin-Helmholtz instability with a uniform scale, while vortex stretching and distortion are significantly more severe in Stage II. For M_c = 0.47, Stage I contains no discernible coherent structures, due to the generation of relatively small-scale structures at this high convective Mach number; but at stage II, large-scale motions become dominant, hence one observes a smaller growth rate in this stage. Thus, it is interesting that a lower growth rate is associated with large-scale vortices at both M_c.

In addition, the effects of incoming boundary layersare observed by studying the relation between the scale of the boundary layers and the growth rate. The study presents that, besides compressibility effects, the inflow condition also accounts for the magnitude of the growth rate. The results show that the GLEAM is effective in quantifying the thickness of CML,and may be applied tothe investigation of the ensemble property of other compressible shear flows.

See the article: Wang T J, Chen J, Shi X T, et al. Experimental evidence for non-linear growth in compressible mixing layer. Sci China-Phys Mech Astron, 2014, 57: 963–970, doi:10.1007/s11433-014-5432-2

http://phys.scichina.com:8083/sciGe/EN/abstract/abstract508794.shtml