Metropolis Hastings抽样法示例

## 解答：

mvdnorm <- function(x, mu, sigma){

    #从x减去mu

    x.minus.mu <- x - mu 

    exp.arg    <- -0.5 * sum(x.minus.mu * solve(sigma, x.minus.mu))  

    # det(sigma) sigma 的行列式

    return( 1 / (2 * pi * sqrt(det(sigma))) * exp(exp.arg) )

}

 

## 问题二

## 假设二元正态分布的参数如下： 

## 两个维度的平均值分别为 2， 3

# 协方差矩阵为

# 4 1

# 1 4

# 尝试用蒙特卡洛马尔科夫链 Metropolis Hastings 抽样法生成后验分布，进行10000次随机抽样，并计算随机点的接受率。

 

# 答： 按照题意，有

mu <- c(2 ,3)

sigma <- matrix(c(4, 1, 1, 4), nrow = 2)

 

# 限制sampler在空间的移动速率，数值越大，变化越快，该数值的设定待进一步讨论。

 

sd.proposal <- 2

 

## 设定模拟的次数

n <- 10000

## 生成NA组成的矩阵，用于保存模拟的结果

x <- matrix(nrow = n, ncol = 2)

 

# 设定sampler的初始值，假定数据点从 0, 0开始 （实际上该sampler可以从任意点开始移动）

cur.x <- c(0, 0)

 

# 计算给定初始值时的概率密度

cur.f <- mvdnorm(cur.x, mu, sigma)

 

### 蒙特卡洛马尔科夫链

n.accepted <- 0

for(i in 1:n){

    new.x <- cur.x + sd.proposal * rnorm(2)  ## 随机生成x

    new.f <- mvdnorm(new.x, mu, sigma)       ## 计算概率密度

    if(runif(1) < new.f/cur.f){  

        ## new.f/cur.f 概率密度的比率 和 (0,1)之间的随机数相比

        ## 若该比率小于随机数，则接受该点

       n.accepted <- n.accepted + 1

       cur.x <- new.x

       cur.f <- new.f

       }

    x[i,] <- cur.x                            ## 将cur.x存到第i行

}

 

#查看接受率

n.accepted/n

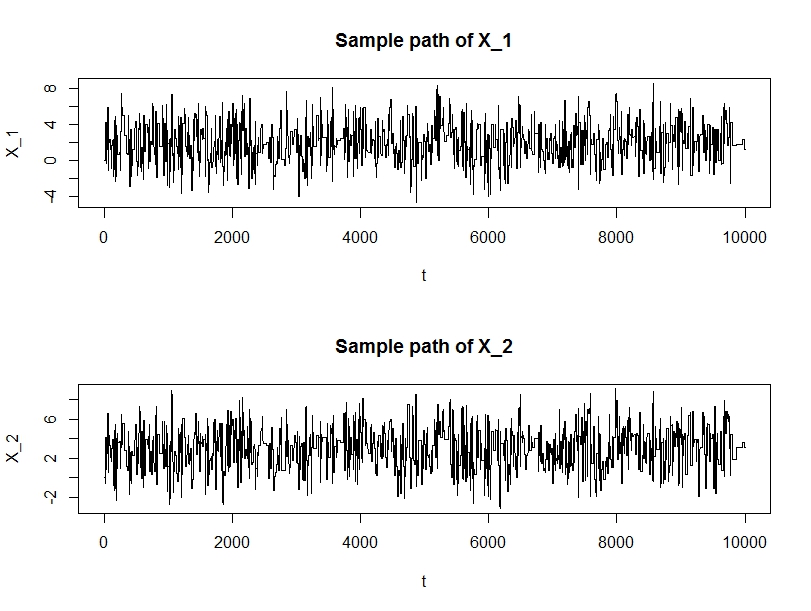
 #查看每个变量的随机变化情况

par(mfrow=c(2,1))

plot(x[,1], type="l", xlab="t", ylab="X_1", main="Sample path of X_1")

plot(x[,2], type="l", xlab="t", ylab="X_2", main="Sample path of X_2")

 

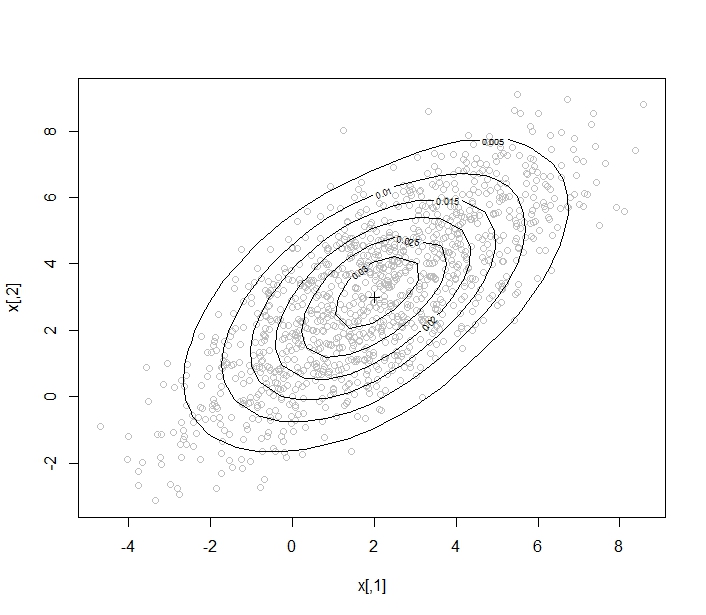
## 绘制椭圆概率密度图

library(MASS)

proline.density <- kde2d(x[,1], x[,2], h = 5)

par(mfrow = c(1, 1))

plot(x, col = "gray")

contour(proline.density, add = TRUE)

points(2,3, pch = 3)

转载本文请联系原作者获取授权，同时请注明本文来自张金龙科学网博客。
链接地址：https://blog.sciencenet.cn/blog-255662-542389.html

上一篇：将比对好的fasta序列转换成relaxed phylip格式
下一篇：于默奥的蓝天白云