博文
相关逻辑 (4) - 形式语言  精选
精选
||
[敬请读者注意] 本人保留本文的全部著作权利。如果哪位读者使用本文所描述内容,请务必如实引用并明白注明本文出处。如果本人发现任何人擅自使用本文任何部分内容而不明白注明出处,恕本人在网上广泛公布侵权者姓名。敬请各位读者注意,谢谢!
相关逻辑 (4) - 形式语言
程京德
自20世纪50年代起至今,相关逻辑(Relevant/Relevance Logic)已经发展成为哲学逻辑中一个非常重要的分支。笔者主张,相关逻辑必将成为支撑智能科学及人工智能技术的统一理论之逻辑基础。本系列文章将全面介绍相关逻辑及其应用。
命题相关逻辑的形式语言
命题相关逻辑的符号表由初始逻辑联结词,逻辑常数(恒真和恒假),辅助括号,以及命题变量的可数集构成:{ =>(本文用于表达内涵联结词“必然归约(entailment)”或“相关蕴涵(relevant implication)”), !(本文用于表达真值函数联结词“否定(negation)”), &(本文用于表达外延真值函数联结词“联言/合取(conjunction)”), TT(本文用于表达逻辑常数恒真), FF(本文用于表达逻辑常数恒假), (, ), p1, p2, …,pn,… (本文用 PV = {p1, p2, …,pn, … } 表达命题变量符号的可数集) }。
用初始逻辑联结词定义的联结词有:内涵联言(intensional conjunction),内涵选言(intensional disjunction),内涵等价(intensional equivalence),外延真值函数选言(extensional disjunction),外延真值函数实质蕴含(material implication),外延真值函数等价(extensional equivalence),必然性模态算子(necessity operator)。由于微信公众号和科学网博客的符号表达困难,这里就不一一详细列举了,请读者参阅下图。
命题相关逻辑的逻辑式/公式(Formulas, Well-formed formulas, wffs)定义如下:
(1) 每个命题变量、TT、FF 都是一个逻辑式/公式,并被称为原子逻辑式/公式(atomic formula);
(2) 如果 A 和 B 是逻辑式/公式,那么 (A=>B),(!A),(A&B) 也是逻辑式/公式;
(3) 仅由上述两种方式构成的是逻辑式/公式。
我们用 WFF 来表达由所有逻辑式/公式构成的可数集。
所以,命题相关逻辑的形式语言是一个九元组 ( =>, !, &, TT, FF, (, ), PV, WFF )。
一阶谓词相关逻辑的形式语言
一阶谓词相关逻辑的符号表由初始逻辑联结词,逻辑常数(恒真和恒假),辅助括号,个体常量的可数集,个体变量的可数集,函数符号的可数集,以及谓词符号的可数集构成:{ =>(本文用于表达内涵联结词“必然归约(entailment)”或“相关蕴涵(relevant implication)”), !(本文用于表达真值函数联结词“否定(negation)”), &(本文用于表达外延真值函数联结词“联言/合取(conjunction)”), TT(本文用于表达逻辑常数恒真), FF(本文用于表达逻辑常数恒假),FA(本文用于表达全称量词),(, ), x1, x2, …, xn, … (本文用 IV= {x1, x2, …, xn, … } 表达个体变量符号的可数集), c1, c2, …, cn, … (本文用 IC= {c1, c2, …, cn, … } 表达个体常量符号的可数集), f11, …, f1n, …, f21, …, f2n, …, fk1, …, fkn, … (本文用 Fun = { f11, …, f1n, …, f21, …, f2n, …, fk1, …, fkn,, …, fkn,… } 表达 1元, 2元, …, n元,… 函数符号的可数集), p01, …, p0n, …, p11, …, p1n, …, p21, …, p2n, …, pk1,…, pkn,… (本文用 Pre = {p01, …, p0n, …, p11, …, p1n, …, p21, …, p2n, …, pk1,…, pkn,… } 表达表达 0元,1元,2元, …, n元,… 谓词符号的可数集) }。
一阶谓词相关逻辑的项(Terms)定义如下:
(1) 每个个体常量和每个个体变量都是一个项;
(2) 如果 f 是一个 n 元函数符号,t1, t2, …, tn 都是项,那么 f(t1, t2, …, tn) 是一个项;
(3) 仅由上述两种方式构成的是项。
如果一个项里面不包含有个体变量,则称其为封闭项(closed/variable-free/ground term)。
我们用 Ter 来表达由所有项构成的可数集。
一阶谓词相关逻辑的逻辑式/公式(Formulas, Well-formed formulas, wffs)定义如下:
(1) 如果 p 是一个 n 元谓词符号,t1, t2, …, tn 都是项,那么 p(t1, t2, …, tn)、TT、FF都是一个逻辑式/公式,并被称为原子逻辑式/公式(atomic formula);
(2) 如果 A 和 B 是逻辑式/公式,x 是一个个体变量,那么 (A=>B),(!A),(A&B),((FAx)A) 也是逻辑式/公式;
(3) 仅由上述两种方式构成的是逻辑式/公式。
如果一个逻辑式/公式里面不包含有量词,则称其为开放逻辑式/公式(open formula)。
我们用 WFF 来表达由所有逻辑式/公式构成的可数集。
所以,一阶谓词相关逻辑的形式语言是一个十四元组 ( =>, !, &, TT, FF, FA, (, ), IV, IC, Fun, Pre, Ter, WFF )。
逻辑式/公式之关于蕴涵关系的度
针对相关逻辑中最重要的初始内涵联结词“必然归约(entailment)”以及“相关蕴涵(relevant implication)”,相关逻辑学家引入了“度(degree)”的概念来表达蕴涵关系在一个逻辑式/公式中的嵌套深度 [1,2]。“度(degree)”的概念在相关逻辑的证明论中起到重要的作用。另外,根据笔者对相关逻辑之应用的研究,“度(degree)”的概念在应用实践中也起到非常重要的作用 [3]。
简单地说,一个不包含有初始内涵联结词“必然归约(entailment)”或“相关蕴涵(relevant implication)”的逻辑式/公式被称为是“零度(zero degree)”的。所以,“零度(zero degree)”的逻辑式/公式是所有的原子逻辑式/公式以及以这些原子逻辑式/公式作为子式用外延真值函数联结词组合而成的复合逻辑式/公式。
其前件和后件都是“零度(zero degree)”逻辑式/公式的一个条件句或蕴涵逻辑式/公式被称为是“第一度(first degree)”条件句或蕴涵逻辑式/公式;以“零度(zero degree)”的逻辑式/公式以及“第一度(first degree)”条件句或蕴涵逻辑式/公式作为子式用外延真值函数联结词组合而成的复合逻辑式/公式被称为是“第一度(first degree)”逻辑式/公式。
类似地可以定义“第二度(second degree)”逻辑式/公式,“第 k 度(kth degree)”逻辑式/公式,详见下图。
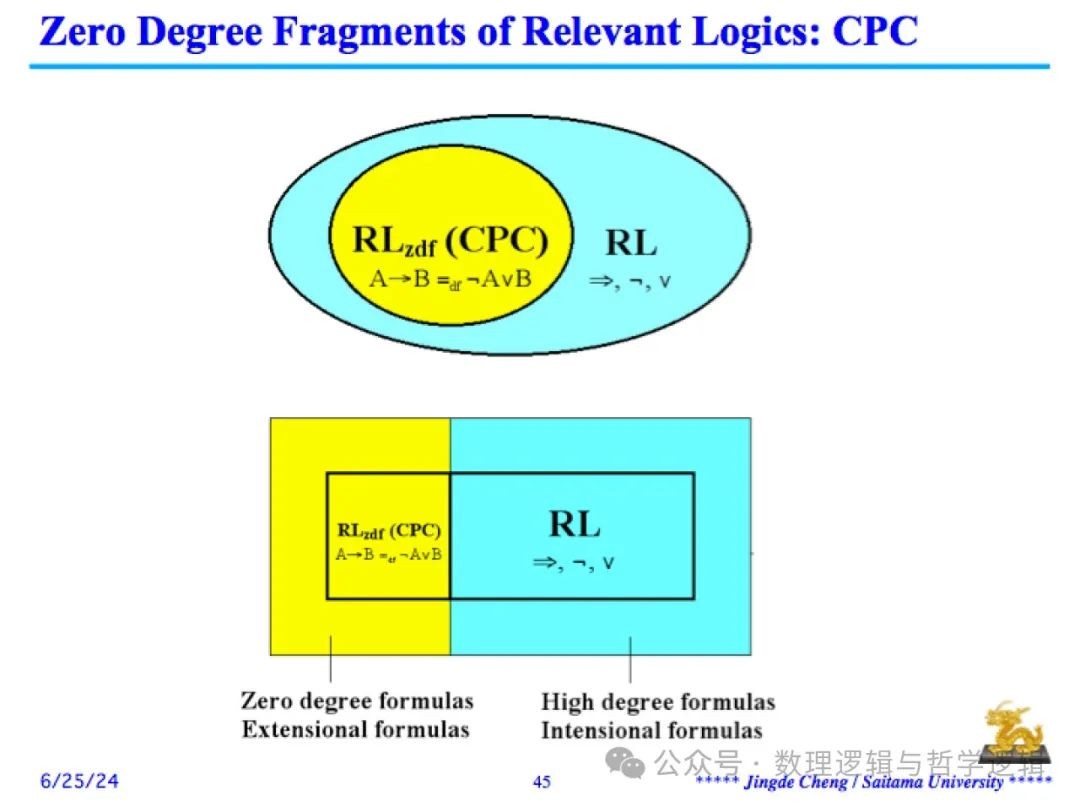
相关逻辑学家们证明的一个重要理论结果是:相关逻辑 E 和 R 是经典数理逻辑的保存扩张;相关逻辑 E 和 R 的逻辑定理集合的“零度片段(zero degree fragment)” 恰好就是经典数理逻辑的逻辑定理集合。请参阅上图。
当然,上述理论结果仅仅揭示了相关逻辑与经典数理逻辑之间的关系,其逻辑定理集合的“零度片段(zero degree fragment)”中的逻辑定理并非能够用来表达有效的推理,因为在相关逻辑中,条件句是用初始内涵联结词“必然归约(entailment)”或“相关蕴涵(relevant implication)”而并非用经典数理逻辑的实质蕴涵来表达的。这一点与那些经典数理逻辑的“经典”保存扩张逻辑系统在本质上完全不同。
参考文献
[1] A. R. Anderson and N. D. Belnap Jr., “Entailment: The Logic of Relevance and Necessity,” Vol. I, Princeton University Press, Princeton, 1975.
[2] A. R. Anderson, N. D. Belnap Jr., and J. M. Dunn, “Entailment: The Logic of Relevance and Necessity,” Vol. II, Princeton University Press, Princeton, 1992.
[3] 程京德,“强相关逻辑及其应用(上)、(中)、(下)”,微信公众号“数理逻辑与哲学逻辑”,科学网博客,2023年6月18日、2023年8月8日、2023年8月12日。
微信公众号“数理逻辑与哲学逻辑”
https://blog.sciencenet.cn/blog-2371919-1439596.html
上一篇:相关逻辑 (3) - 特征
下一篇:准确地理解哥德尔不完全性定理“关于PM及相关系统的形式不可判定命题”(1) - 背景及内容