[敬请读者注意] 本人保留本文的全部著作权利。如果哪位读者使用本文所描述内容，请务必如实引用并明白注明本文出处。如果本人发现任何人擅自使用本文任何部分内容而不明白注明出处，恕本人在网上广泛公布侵权者姓名。敬请各位读者注意，谢谢！

相关逻辑 (3) - 特征

程京德 

自20世纪50年代起至今，相关逻辑(Relevant/Relevance Logic)已经发展成为哲学逻辑中一个非常重要的分支。笔者主张，相关逻辑必将成为支撑智能科学及人工智能技术的统一理论之逻辑基础。本系列文章将全面介绍相关逻辑及其应用。

相关逻辑之本质特征：何谓“相关逻辑”？

何谓“相关逻辑”？或者换言之，使得相关逻辑区别于其它形式逻辑系统的本质特征为何？对于这个问题，从不同的观点来考查，将会得到不同的答案。

如同我们已经介绍过的，相关逻辑创建的背景是：“‘条件句’概念在我们人类文化中至关重要，但是时至今日却仍然没有一个让各个领域学者们一致认可的准确清晰定义，各类逻辑系统均对其之表达有着不同的观点和形式，形式化的经典数理逻辑系统和经典模态逻辑系统中都存在有被称为‘蕴涵悖论’的、与我们人类日常思维直觉相悖的逻辑定理。因此，当然就有思想敏锐、责任感强烈的逻辑学家/哲学家们持续不断地努力试图解决这个难题。这就是相关逻辑创生的历史背景。”[1-3]。

阿克曼、安德森、贝尔纳普等逻辑学家创建和发展相关逻辑的初始动机就是为了排除蕴涵悖论[1-13]。阿克曼在其开创性论文中陈述：“C. I. Lewis 在通常蕴涵之外引入严格蕴涵的原因是众所周知的。在本文的工作中，出于类似的原因引入了严密蕴涵[strenge Implikation, rigorous implication]，但它是一个比严格蕴涵更狭义的概念。(Die Gründe, die C. I. Lewis bewogen haben, neben der gewöhnlichen Implikation eine strikte Implikation einzuführen, sind bekannt. In der vorliegenden Arbeit wird aus ähnlichen Gründen eine strenge Implikation eingeführt, die jedoch einen engeren Begriff darstellt als die strikte Implikation.) (The reasons that led C. I. Lewis to introduce a strict implication in addition to the usual implication are well known. In the present work, a rigorous implication [strenge Implikation] is introduced for similar reasons, but this is a narrower concept than the strict implication.)”[5]  如同安德森和贝尔纳普所述：“他[阿克曼]的 Strengen Implikation 的系统的主要优点之一是，它和它的近邻系统第一次给了我们一个理解‘如果…那么—’命题中前件与后件之间难以捉摸的相关性的、在数学上令人满意的方法。(one of the principal merits of his system of strengen Implikation is that it, and its neighbors, give us for the first time a mathematically satisfactory way of grasping the elusive notion of relevance of antecedent to consequent in “if … then --” propositions)”；“认为相关性与有效性无关的想法让我们觉得可笑，因此我们试图解释 A 与 B 的相关性概念。(The fancy that relevance is irrelevant to validity strikes us as ludicrous, and we therefore make an attempt to explicate the notion of relevance of A to B.)”[6]。

因此，笔者认为，首先从解决条件句/蕴涵关系表达以及蕴涵悖论问题的观点来归纳相关逻辑的本质特征是合适的。

关于条件句/蕴涵关系之前件与后件之间的相关性，是从古希腊亚里士多德时代(亚里士多德(Aristotle, 384-322 BC)，塞克斯都·恩披里柯(Sextus Empiricus, 160-210))就一直被哲学家逻辑学家们所关心和讨论的问题 [6,8,14]。弗雷格和罗素（及怀德海）对经典数理逻辑进行形式化公理化的工作，完全忽视了条件句/蕴涵关系之前件与后件之间的相关性而将“实质蕴涵”定义为一个真值函数，由此引发了“蕴涵悖论”问题 [1-14]。

笔者认为，从解决条件句/蕴涵关系表达以及蕴涵悖论的观点来看，使得相关逻辑区别于其它形形色色的形式逻辑系统的本质特征为：相关逻辑是唯一的一族形式逻辑系统，其创建动机在于试图要解决条件句/蕴涵关系之前件与后件之间的相关性问题，其每个成员都从逻辑定理中完全排除了（经典数理逻辑的）实质蕴涵悖论和（刘易斯模态逻辑的）严格蕴涵悖论。

由弗雷格和罗素（及怀德海）建立的经典数理逻辑完全忽视了条件句/蕴涵关系之前件与后件之间的相关性而仅从真假值来定义实质蕴涵，由刘易斯建立的模态逻辑也完全忽视了条件句/蕴涵关系之前件与后件之间的相关性而以引入“不可能”/“必然”模态算子来定义严格蕴涵，故而它们在本质上都完全不同于相关逻辑。经典数理逻辑或刘易斯模态逻辑的各种保存扩张系统当然也都完全不同于相关逻辑。

但是，当然也有逻辑学家以不同的哲学/逻辑学观点和具体标准来界定相关逻辑。

美国逻辑学家 Dunn 认为，“到目前为止，有许多形式系统可以说是‘相关逻辑’。其中一些早于安德森-贝尔纳普方法，一些是最近的方法。(There are by now a host of formal systems that can be said with some justification to be ‘relevance logics’. Some of these antedate the Anderson-Belnap approach, some are more recent.)” [15]  尽管 Dunn 并没有给出一个清晰具体标准来界定他所认可的“相关逻辑”，但是他也陈述了“安德森-贝尔纳普方法的相关逻辑”的特征：“这些系统 [ E 和 R ] 中的每一个关注于形式化一类蕴涵（或条件句），在这类蕴涵中，前件对于后件来说足够相关。(each of these [E 和 R] is concerned to formalize a species of implication (or conditional) in which the antecedent suffices relevantly for the consequent.)” [15] 

Dunn 和 澳大利亚逻辑学家 Restall 认为，“近年来，可以清晰地认识到，相关逻辑非常适合被容纳入‘资源意识’或‘子结构’逻辑这一更广泛的类别。 (in the recent years it has become clear that relevance logics fit well among a wider class of ‘resource-conscious’ or ‘substructural’ logics.)” [16] 亦即，Dunn 和 Restall 把相关逻辑归类于‘资源意识’或‘子结构’逻辑的子类。笔者认为，尽管这样地把相关逻辑进行归类在理论上/技术上是可行的，但是这种归类太多地强调了相关逻辑的形式系统侧面而完全忽略了相关逻辑的初始创建动机，从目的（解决条件句/蕴涵关系表达的问题）和应用（建立合理的推理有效性评价标准）两方面来说，未必合适。

一个比较极端的例子是，把凡是不包含 A → (B → A)（通称，“positive paradox”）作为逻辑公理或定理的逻辑系统都视为相关逻辑：“我们使用术语‘相关逻辑’主要是指不包含 A → (B → A) 作为公理(或定理)的逻辑。 (we use the term ‘relevance logics’ primarily to refer to logics that do not contain A → (B → A) as an axiom (or a theorem).)”[16] 在这种观点之下，线性逻辑也可以被视为相关逻辑：“最近引入的相关逻辑之一是线性逻辑 L，它实际上为早期的相关逻辑之一添加了一个模态。(One of the relevance logics most recently introduced is linear logic L, which in effect adds a modality to one of the earlier relevance logics.)”[17] 

变量共享/相关性原理：相关逻辑的形式特征 

通常认为，经典数理逻辑的形式化过程中完全忽视了条件句/蕴涵关系之前件与后件之间的相关性是因为这种相关性是难以捉摸、难以形式化的。在相关逻辑创建初期，对相关逻辑持否定态度的逻辑学家们的主要反对理由也在于此。如同安德森和贝尔纳普所述：“事实上，用外延逻辑处理的同样程度的数学复杂性和精确性来处理相关性的困难导致许多有影响力的哲学家-逻辑学家认为，不可能找到一个令人满意的处理这个问题的方法。结果，在过去的三十年里，许多最敏锐的逻辑学家都在一面哲学旗帜下游行，上面写着“一般地打倒相关性、意义和内涵！(Indeed the difficulty of treating relevance with the same degree of mathematical sophistication and exactness characteristic of treatments of extensional logic led many influential philosopher-logicians to believe that it was impossible to find a satisfactory treatment of the topic. And in consequence, many of the most acute logicians in the past thirty years have marched under a philosophical banner reading “Down with relevance, meanings, and intensions generally!”)”[6] 

然而，相关逻辑学家们近乎完美地解决了相关性的形式化问题。

各个相关逻辑系统完全排除实质蕴涵悖论和严格蕴涵悖论的理论保证在于“变量共享/相关性原理(The Variable-sharing/Relevance Principle)”[6-8,11-13]：一个条件句形式的相关逻辑定理的前件与后件之间必须共享至少一个命题变量（更加详细的形式化定义和说明将在本系列后续文章中给出）。

变量共享/相关性原理在形式上保证了在相关逻辑中恒真条件句命题的前件后件之间的必然相关性，这是所有相关逻辑系统必然满足的本质特征，因此就是一个形式逻辑系统可以被称为/归为相关逻辑的必要条件。正是因为所有相关逻辑系统的逻辑定理都必然地满足变量共享/相关性原理，其条件句形式逻辑定理的前件后件之间都共享至少一个命题变量，所以，那些前件后件之间毫不相关的、被称之为最典型最难排除的蕴涵悖论就从相关逻辑系统逻辑定理中全都被排除掉了。

必须注意：变量共享/相关性原理只是一个形式逻辑系统可以被算作相关逻辑的必要条件，但并非充分条件。有些条件句公式虽然满足变量共享，但仍然未必是相关逻辑的逻辑定理甚至根本就是逻辑谬误。所以，变量共享/相关性原理并没有给我们提供一个排除所有悖论和谬误的判定标准，也没有告诉我们究竟什么应该是“真正的”条件句/蕴涵关系（本系列后续文章将会讨论“强变量共享/强相关性原理”，有兴趣的读者可以预先参阅笔者有关“强相关逻辑”的文章[2,18,19]）。然而，相关逻辑确实为我们提供了“一个前提必须在演绎过程中实际上被使用”这种意义上的相关的演绎证明概念。

新西兰逻辑学家 Mares 和澳大利亚逻辑学家 Meyer 曾经归纳给出相关逻辑系统应该满足的三个条件：“相关逻辑应该满足三个条件:  1. 它们应该避免蕴涵悖论，特别是给出一种处理矛盾和其他不可能的方法。  2. 它们应该满足“变量共享约束”。  3. 它们应该包含一个演绎可能性关系，要求一个有效的演绎中的所有前提都能够被用在了那个演绎之中，并且它们应该满足一个演绎定理。 (relevant logics should satisfy three conditions:  1. They should avoid the paradoxes of implication and, in particular, give a way of dealing with contradictions and other impossibilities non-trivially.  2. They should satisfy the ‘variable sharing constraint’.  3. They should contain a deducibility relation that requires all premises in a valid deduction to be capable of being used in that deduction and they should satisfy a deduction theorem.)”[12]  

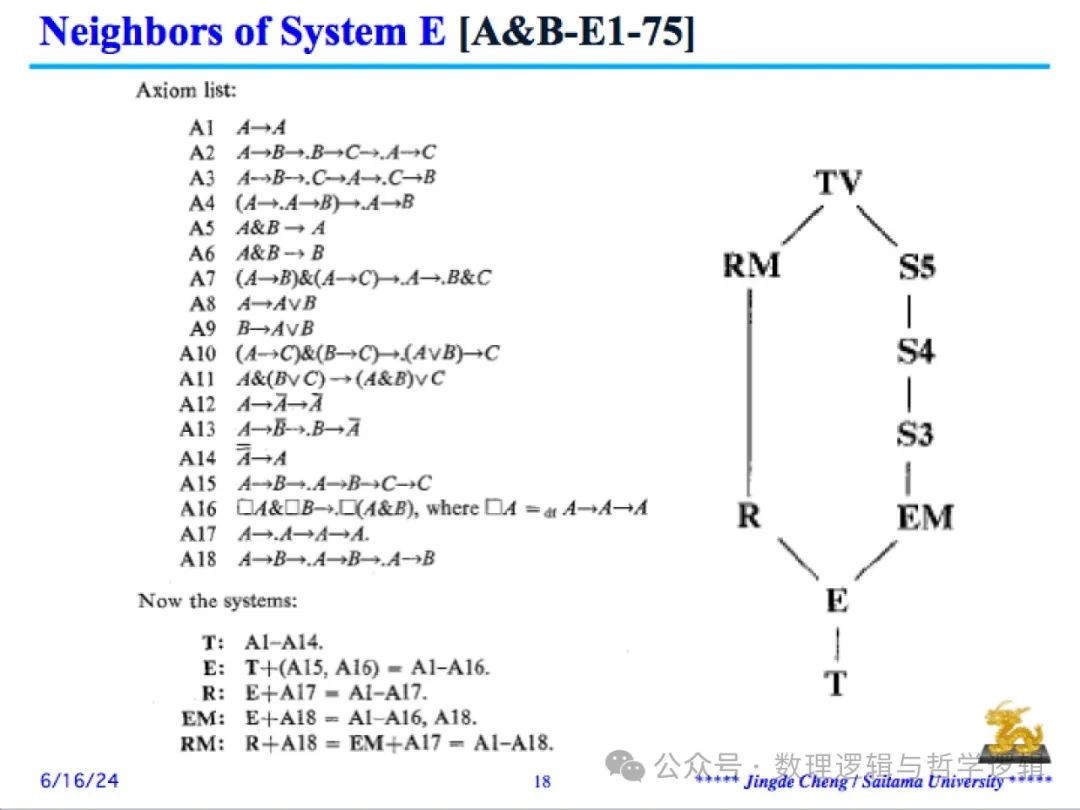
主要的/标准的相关逻辑系统 E 和 R 

尽管阿克曼最早提出的第一个完整的相关逻辑形式系统是 π’，但是从上个世纪50年代创建初期起，相关逻辑学家们主要的/标准的研究对象就一直是安德森和贝尔纳普提出的系统 E 以及贝尔纳普提出的系统 R [5-13,15,16]。

安德森和贝尔纳普提出的相关逻辑形式系统 E 是从阿克曼的相关逻辑形式系统 π’ 中去除了推理规则 (γ) （选言/析取三段论）并用一个公理替换掉推理规则 (δ) 之后得到的一个等价系统 [6-8,10,15,16]。因为阿克曼的系统 π’ 是对刘易斯的模态逻辑系统 S4 的弱化（为了排除严格蕴涵悖论）[5-7,10]，与 π’ 等价的 E 当然也就保留有模态性质（必然性），故而文献中常常可以见到 “System E of entailment”、“System E of relevant entailment”、“System E of relevant strict implication”、“System E of strict relevant implication”的称呼。

如同我们已经说明过的，与刘易斯在经典数理逻辑（外延真值函数逻辑）的形式语言中引入模态算子来定义“严格蕴涵”的方法不同，阿克曼没有在形式语言中引入模态算子，而是直接引入一个内涵逻辑联结词作为初始联结词（这里我们用“=>”表示）来表达条件句/蕴涵关系。为了让 E 的模态性质更明晰地显示出来，安德森和贝尔纳普在 E 中是用条件句/蕴涵式来定义必然性模态算子的：LA =_df(A => A) => A (where L is the necessity operator)。 本系列后续文章中将有专文介绍相关逻辑的模态性质，有兴趣的读者可以先参阅一下安德森和贝尔纳普对系统 E 的公理化中的“Distribution of necessity over conjunction”公理模式 E7。 

与具有模态性质的相关逻辑系统 E 不同，为了研究“纯相关性”的逻辑系统，贝尔纳普提出了相关逻辑系统 R [6,7]。 R 是在 E 的基础上加上公理模式 A => ((A => A) => A)（亦即，A => LA，从必然性模态的观点看，这是一个必然性模态谬误）而得到的“纯”相关逻辑（E 原有的必然性模态性质被破坏了）[6,7]。 R 的初始内涵逻辑联结词表达的蕴涵关系被称为“相关蕴涵(relevant implication)”[6-10]。

既然有了“纯”相关逻辑系统 R，那么自然就有逻辑学家会想到在 R 的形式语言中引入一个必然性模态算子来定义“必然的相关蕴涵”并构建一个模态相关逻辑系统来刻画其性质。 澳大利亚逻辑学家 Mayer 定义了这样的一个模态相关逻辑系统 NR 并且很自然地猜测 NR 等价于 E 以及阿克曼的 π’，认为这三个系统恰好刻画了“必然归结(entailment)”这个概念 [6-9]。但是，经过其它逻辑学家调查发现，NR 和 E 并不完全等价，NR 中含有并非 E 之逻辑定理的逻辑定理，从而证明 Mayer 的“必然的相关蕴涵”并非就是 E 的“必然归结(entailment)”，两者不尽相同 [6-9]。

结语 

条件句是逻辑学中最核心的概念，相关逻辑以试图解决条件句/蕴涵关系之前件与后件之间的相关性问题为创建动机并且基本解决了该问题，完全排除了实质蕴含悖论和严格蕴涵悖论，为逻辑推理有效性判定标准提供了比经典数理逻辑和刘易斯模态逻辑更加合理的的形式逻辑系统。所以，相关逻辑在整个逻辑学中乃至对于哲学、数学、科学来说，远非仅为现代哲学逻辑之一分支这样的地位，而是具有极其重要的核心地位。

基于对相关逻辑的学习及理解和笔者本人的研究及思考[18-25]，笔者主张并且相信，相关逻辑必将成为支撑智能科学及人工智能技术的统一理论（如果的确可以构建起来的话）之逻辑基础。

本系列后续文章将逐步介绍相关逻辑的形式化细节。

参考文献 

[1] 程京德，“条件句：逻辑学中的最核心概念及最大难题”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年1月29日。

[2] 程京德，“悖论集锦(2) – 作为逻辑学中最大难题的蕴涵悖论问题（上）”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2024年3月18日；悖论集锦(2) – 作为逻辑学中最大难题的蕴涵悖论问题（上）（修订增补版）”，微信公众号“数理逻辑与哲学逻辑”，2023年4月11日；“悖论集锦(2) - 作为逻辑学中最大难题的蕴涵悖论问题（下）”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2024年4月18日。

[3] 程京德，“相关逻辑 (1) - 背景与前史”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2024年5月28日。

[4] 程京德，“相关逻辑 (2) – 创建”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2024年6月9日。

[5] W. Ackermann, “Begründung Einer Strengen Implikation,” The Journal of Symbolic Logic, Vol. 21, pp. 113-128, 1956 (in German). 

[6] A. R. Anderson and N. D. Belnap Jr., “Entailment: The Logic of Relevance and Necessity,” Vol. I, Princeton University Press, Princeton, 1975. 

[7] A. R. Anderson， N. D. Belnap Jr., and J. M. Dunn, “Entailment: The Logic of Relevance and Necessity,” Vol. II, Princeton University Press, Princeton, 1992.

[8] S. Read, “Relevant Logic: A Philosophical Examination of Inference,” Basil Blackwell, Oxford, 1988, 2012. 

[9] E. D. Mares, “Relevant Logic: A Philosophical Interpretation,” Cambridge University Press, Cambridge, 2004. 

[10] G. Restall, “Relevant and Substructural Logics,” in D. M. Gabbay and J. Woods (Eds.), “Handbook of the History of Logic, Vol. 7: Logic and the Modalities in the Twentieth Century,” pp. 289-398, Elsevier B.V., Amsterdam, 2006. 

[11] E. D. Mares, “Relevance Logic,” The Stanford Encyclopedia of Philosophy, Center for the Study of Language and Information (CSLI), Stanford University, 1998-2020.

[12] E. D. Mares and R. K. Meyer, “Relevant Logics,” in L. Goble (Ed.), “The Blackwell Guide to Philosophical Logic,” pp. 280-308, Blackwell, Oxford, 2001. 

[13] E. D. Mares, “Relevance Logic,” in D. Jacquette (Ed.), “A Companion to Philosophical Logic,” pp. 609-627, Blackwell, Oxford, 2002. 

[14] 山川偉也，“条件文についての古代の論争 - メガラ・ストア論理学の理解のために”，桃山学院大学，1981。

[15] J. M. Dunn, “Relevance Logic and Entailment,” in D. Gabbay and F. Guenthner (eds.), “Handbook of Philosophical Logic,” Vol. III, pp. 117-224, D. Reidel, Dordrecht, 1986. 

[16] J. M. Dunn and G. Restall, “Relevance Logic,” in D. Gabbay and F. Guenthner (Eds.), “Handbook of Philosophical Logic, 2nd Edition,” Vol. 6, pp. 1-128, Kluwer Academic, Dordrecht, 2002. 

[17] K. Bimbo, “Relevance Logics,” in D. Jacquette (Ed.), “Philosophy of Logic,” pp. 723-789, Elsevier B. V., Amsterdam, 2007. 

[18] 程京德，“相关推论与强相关逻辑”，科技导报，Vol. 34, No. 7, pp. 39-47, 2016. 

[19] 程京德，“强相关逻辑及其应用（上）、（中）、（下）”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年6月18日、2023年8月8日、2023年8月12日。

[20] 程京德，“逻辑学之重要性（及对其在中国被轻视之原因初探）”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年1月27日。 

[21] 程京德, “形象思维、抽象思维及逻辑思维”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年8月19日。 

[22] 程京德, “如何培育和提高逻辑思维能力？”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年8月23日。

[23] 程京德, “为什么说逻辑推理能力是人类智能中最基本的能力？”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年10月24日。 

[24] 程京德，“现代逻辑之未来 - 从相关逻辑到量子逻辑（纲要）”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年7月25日。

[25] 程京德，“实现人工通用智能的关键必由之路 - 基于强相关逻辑的形式理论自动定理发现”，微信公众号“数理逻辑与哲学逻辑”，科学网博客，2023年10月19日。

微信公众号“数理逻辑与哲学逻辑”