博文
哲学逻辑(2) – 模态逻辑
||
[敬请读者注意] 本人保留本文的全部著作权利。如果哪位读者使用本文所描述内容,请务必如实引用并明白注明本文出处。如果本人发现任何人擅自使用本文任何部分内容而不明白注明出处,恕本人在网上广泛公布侵权者姓名。敬请各位读者注意,谢谢!
哲学逻辑(2) – 模态逻辑
程京德
模态逻辑(Madol Logic)
“美国逻辑学家刘易斯(Clarence Irving Lewis)是现代模态逻辑的创始人,但其实上他的工作的最初目的就是改造经典数理逻辑里的实质蕴涵,试图找到一个可以替代实质蕴涵的新逻辑联结词来更准确地表达条件句。刘易斯认为实质蕴涵没有表达出条件句中的必然性,因此引入了表达必然性的模态算子□来定义用来表达条件句的蕴涵关系,称为严格蕴涵(strict implication)(这里用→3来表达): A→3B =df □(A→B),并且构造了相应的模态逻辑系统S1,S2,S3,S4,S5。”[15]
模态逻辑的目标语言中使用两个模态算子,“必然性”算子(用符号□或者L来表达)和“可能性”算子(用符号◇或者M来表达)。两个算子并非互相独立的,可以互相定义:□A =df not◇notA,◇A =df not□notA 。
由于对于模态算子可以给出不同的哲学解释,所以模态逻辑并非仅有一种而是有许多种。
通常把两个算子解释为“必然/必然真”或者“可能/可能真”的模态逻辑被称为真势模态逻辑(Alethic Modal Logic),这是最原始的模态逻辑,如同上述,始于刘易斯的工作。
在经典数理逻辑基础上通过在目标语言中引入模态算子以及在演绎系统中引入有模态算子修饰的逻辑公理所得到的是经典模态逻辑。如果是在直觉主义逻辑或相关逻辑的基础上通过在目标语言中引入模态算子以及在演绎系统中引入有模态算子修饰的逻辑公理,那么所得到的分别是直觉主义模态逻辑和相关模态逻辑。
在经典数理逻辑命题演算CPC的目标语言中引入模态算子所得到的命题模态逻辑目标语言被称为基本命题模态语言(The basic propositional modal language)。
针对基本命题模态语言的一个结构(frame, Kripke-frame, structure, Kripke-structure)是一个有序对 F =df (W,R),其中 W 是一组非空的对象(可以有各种称呼,比如世界、点、状态),R 是定义在 W 上的一个二元关系。W 通常被称为“世界(world)”的集合,R 通常被称作“可达(accessibility)”关系。
针对基本命题模态语言的一个模型(model)是一个有序对 M =df (F,V) (M = (W, R, V)),F 是一个结构,V 是一个从命题变量集合 φ 到 W 之幂集 P(W) 的评价函数 V: φ → P(W),它对每个命题变量赋予 W 的一个子集,V(p) 意味着在属于该子集的每个世界/点/状态 w,命题变量 p 的真值被赋予为“真”。
给定一个模型 M = (W, R, V),一个命题变量 p(亦即,一个 CPC 原子逻辑式)在该模型的一个世界/点/状态 w 为真当且仅当 w ∈ V(p),一个 CPC 复合逻辑式在 w 为真当且仅当按照 CPC 对逻辑联结词的经典解释定义为真,一个模态逻辑式 □A 为真当且仅当 A 在从 w 可达的所有世界 v (亦即,(所有v)R(w, v))都为真, 一个模态逻辑式 ◇A 为真当且仅当 A 在从 w 可达的某一世界 v (亦即,(存在v)R(w, v))为真。(请参阅下图)
最基本的模态逻辑公理图式是 K(Kripke)公理图式:(K) □(A→B)→(□A→□B) (A和B是任意逻辑式)。
基于经典数理逻辑命题演算 CPC,在目标语言中引入必然模态算子□,在演绎系统中添加公理图式 (K) 以及推理规则必然化规则 N,就得到了最小/最弱的规范(normal)模态逻辑系统 K,K 是 CPC 的保存扩张:K = CPC + (K) + N, Th(K)真包含Th(CPC)。
系统 K 针对所有的结构是健全的和完全的,亦即,每个 K 逻辑定理在任一结构之任一世界的评价都为真,每个恒真的命题模态逻辑式都是 K 的逻辑定理。
系统 K 很弱,许多公认合理的模态逻辑式都不是 K 的逻辑定理,亦即,在 K 不可证。
接下来我们列举其它一些规范模态逻辑系统。
以基本命题模态语言为目标语言,包含有经典数理逻辑命题演算 CPC 的所有公理图式、公理图式 (K)、推理规则分离规则 MP 及必然化规则 N、以及其它一些模态公理图式的逻辑系统,被称为一个规范模态逻辑(Normal Modal Logic)系统。亦即:
NML = CPC + (K) + N + … , Th(NML)真包含Th(K)真包含Th(CPC)
下面是一些模态公理图式以及相应的规范模态逻辑系统:
(D, Deontic) □A→◇A
D(K+D) = K + (D), Th(D)真包含Th(K)
系统 D 关于右无界结构(right-unbounded frames)是健全和完全的(一个结构是右无界的,如果其可达关系 R 是右无界的,亦即,每个世界 w 都有一个后继: (所有x)(存在y)(Rxy) )。
(T) □A→A or A→◇A
T(K+T, K+DT) = K + (T), Th(T)真包含Th(K),
T(K+T, K+DT) = D + (T), Th(T)真包含Th(D)真包含Th(K)
系统 T 关于自反结构(reflexive frames)是健全和完全的(一个结构是自反的,如果其可达关系 R 是自反的)。
(B, Brouwer) A→□◇A
B(K+DTB) = T + B = K + (T) + (B),
Th(B)真包含Th(T)真包含Th(D)真包含Th(K)
系统 B 关于自反对称结构(reflexive and symmetric frames)是健全和完全的(一个结构是自反对称的,如果其可达关系 R 是自反的并且对称的)。
K+B = K + (B), Th(K+B)真包含Th(K)
系统 K+B 关于对称结构(symmetric frames)是健全和完全的(一个结构是对称的,如果其可达关系 R 是对称的)。
(4) □A→□□A or ◇◇A→◇A
K+4 = K + (4), Th(K+4)真包含Th(K)
系统 K+4 关于传递结构(transitive frames)是健全和完全的(一个结构是传递的,如果其可达关系 R 是传递的)。
(5, E, Euclidean) ◇A→□◇A
K+5 = K + (5), Th(K+5)真包含Th(K)
系统 K+5 关于欧几里得结构(Euclidean frames)是健全和完全的(一个结构是欧几里得的,如果其可达关系 R 是欧几里得的,亦即,(所有x)(所有y)(所有z)((Rxy and Rxz) → Ryz) )。
下图显示了各个模态公理图式与结构的关系之性质之间的对应关系。
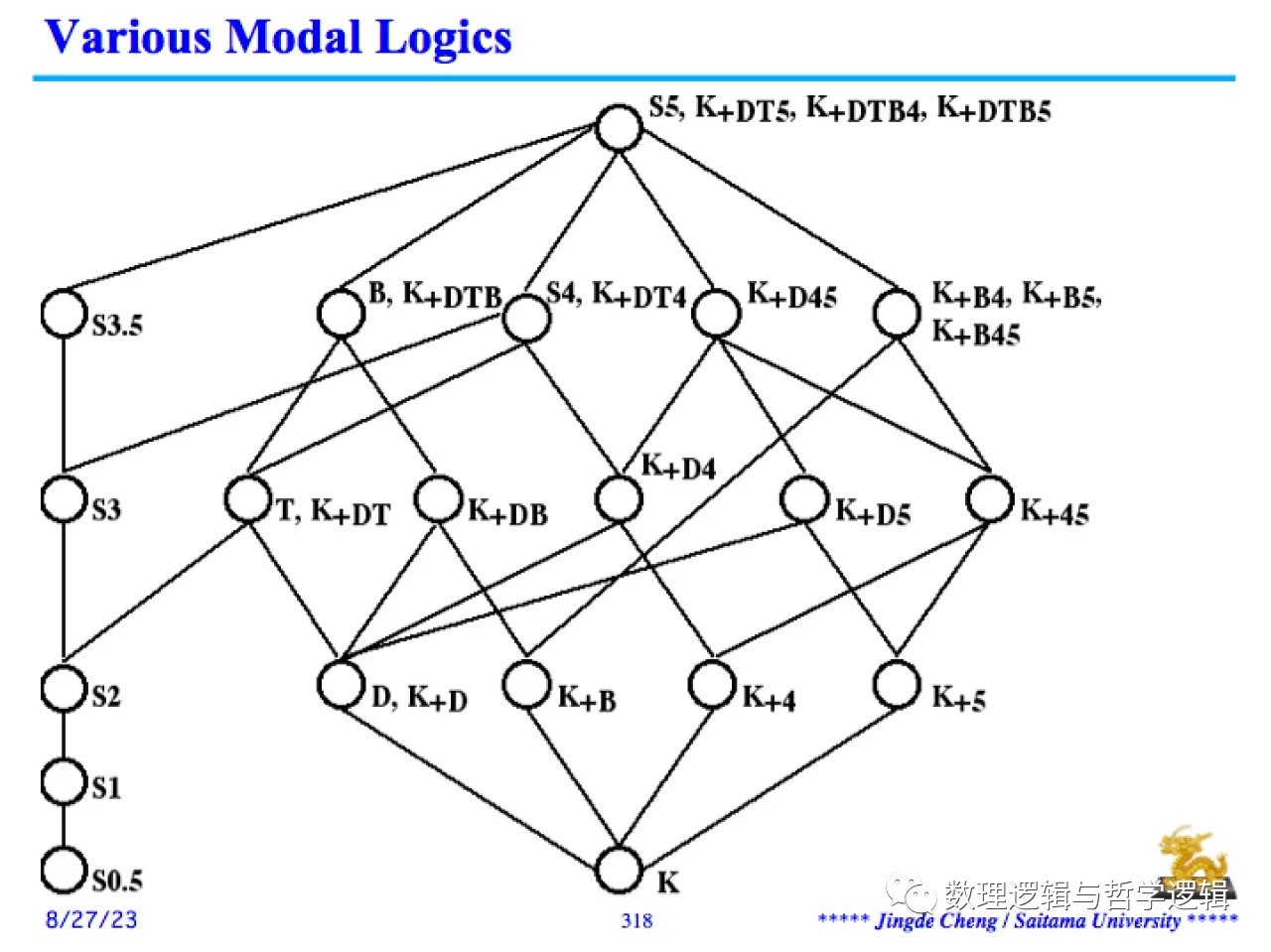
上图显示,各个规范模态逻辑系统之间的偏序包含关系形成了一个代数格(lattice)。我们在上面介绍了模态公理图式 (K),(D),(T),(B),(4),(5(E))以及它们相应的规范模态逻辑系统 K,D,T,B, K+B, K+4, K+5。针对这些规范模态逻辑系统继续添加模态公理图式,可以得到上述代数格中上部的各个规范模态逻辑系统,细节就不在此详述了。
上图还显示了刘易斯的模态逻辑系统与规范模态逻辑系统之间的关系。
真势模态逻辑为关系到必然性和偶然性的论证及推理提供了语言表达手段以及普遍有效性(合理性/正确性)判别标准。但是,如此众多的真势模态逻辑系统,当然提供了不同的判别标准。姑且不论哲学问题,在把真势模态逻辑应用到具体领域时,正确地选择合适的逻辑系统是一个重要的实践问题。
参考文献
[1] 程京德, “逻辑学是什么?” 微信公众号“数理逻辑与哲学逻辑”,2023年1月25日。
[2] 程京德, “为什么在逻辑学中存在有如此众多的不同逻辑系统?” 微信公众号“数理逻辑与哲学逻辑”,2023年1月28日。
[3] W. Kneale and M. Kneale, “The Development of Logic,” Oxford Clarendon Press, 1962, 1984 (Paperback Edition with Corrections); 中译:张家龙,洪汉鼎 译 “逻辑学的发展”,商务印书馆, 1985.
[4] L. Haaparanta (Ed.), “The Development of Modern Logic,” Oxford University Press, 2009.
[5] L. Goble (Ed.), “The Blackwell Guide to Philosophical Logic,” Blackwell, 2001.
[6] D. Jacquette (Ed.),“Blackwell Companions to Philosophy - A Companion to Philosophical Logic,” Blackwell, 2002.
[7] D. M. Gabbay and F. Guenthner (Eds.), “Handbook of Philosophical Logic, 2nd Edition,” Vol.1-18, Springer, 2001-2018.
[8] G. Priest, “An Introduction to Non-Classical Logic, 2nd Edition,” Cambridge University Press, 2008.
[9] D. Jacquette (Ed.),“Philosophy of Logic – An Anthology,” Handbook of the Philosophy of Science, Elsevier, 2007.
[10] W. V. Quine, “Philosophy of Logic, 2nd Edition,” Harvard University Press, 1970, 1986.
[11] S. Haack, “Philosophy of Logics,” Cambridge University Press, 1978; 中译:罗毅 译,张家龙 校,“逻辑哲学”,商务印书馆, 2003.
[12] A. C. Grayling, “An Introduction to Philosophical Logic, 3rd Edition,” Blackwell, 1982, 1990, 1997.
[13] S. Wolffram, “Philosophical Logic – An Introduction,” Routledge, 1989.
[14] S.Read, “Thinking About Logic - An Introduction to the Philosophy of Logic,” OxfordUniversityPress, 1995; 中译:李小五 译,张家龙 校,“对逻辑的思考 - 逻辑哲学导论”,辽宁教育出版社, 1998.
[15] 程京德, “条件句:逻辑学中的最核心概念及最大难题”,微信公众号“数理逻辑与哲学逻辑”,2023年1月29日。
微信公众号“数理逻辑与哲学逻辑”
https://blog.sciencenet.cn/blog-2371919-1400788.html
上一篇:哲学逻辑(1) – 何谓“哲学逻辑”?
下一篇:对 Sam Altman 关于AGI及GPT-10之预言的批评