我和余瑞璜先生的缘分(4)

啥叫缘分？简单地说，缘分就是机缘巧合，但是还需要有灵感来引路。

1996年，我做了大量的X射线衍射实验，证明了程开甲先生的TFDC电子密度确实好用之后，我的物理学触角自然而然地就伸向了余瑞璜先生的EET。

在缘分(3)结尾的时候，我写道：“1988年硕士毕业后，我坚持每年写申请书，每年找人写‘通关文牒’。经过5年的历程，我终于敲开了国家自然科学基金委的大门，1993年我拿到了第1个国家基金项目”。

实际上，1993年敲开基金委的大门，我用的真正的“敲门砖”是魔方，而坚持每年写申请书只是一个必要条件。

缘分就是机缘巧合，但是还需要有灵感来引路。

 1991年冬天，我突发灵感，翻出了1985年丁培柱老师《群论》课的笔记，还有给武钢钢研所搞ODF的推导，在这些工作的基础上，我要搞一个魔方方程，然后用Basic计算机编程，计算出结果后，再用手里的魔方对比，检验我的魔方方程是否正确。

 为什么要突发灵感？因为这年的年号对称，1991，从前往后念，从后往前念，都是1991。10年前在吉大本科毕业时，根据“山东东营”(写成方块相当于二阶魔方)的对称，我来到东营，也许是双重的条件反射，在一个对称的地方，在一个对称的年号，我要研究点对称的东西(魔方)，于是我就真的写出了一本《魔方及其应用》。

 1992年那是一个春天，东营的一家企业资助我，在张兆晋(硕士同学)的帮助下，我的书由中国广播电视出版社出版，这是我的第1本书，也是我的第1本关于魔方的书。

 当时我的数学模型和计算机程序已经现成在手，但是我没有把它们写进书里，因为我认为发表数学模型和计算机程序的时机还不成熟。我也不担心别人在短期内能搞出同样的东西，这一等就是11年，直到2001年我用魔方拿到国家自然科学基金(科普专项)，2003年才把数学模型和魔方程序(三阶、四阶、五阶)全部发表。1992年，我虽然没有把数学模型和计算机程序公开出来，但是，我把“晶体学符号和魔方”的巧妙关系写进书里并且公开发表。这种创意在数学圈子里可能会被不以为然，但是在材料圈子里却属于奇思妙想(魔方和晶体学可以相互表达)。

1993年夏天，我在山东潍坊(潍柴动力)带大学生金工实习(参观)，我准备了两本《魔方及其应用》，已经包装好了，地址邮编和收件人也写好了，随时可以到邮局按照印刷品挂号寄出。因为我已经申请过好几次基金，都没有成功，我对国家基金委的运作机制了如指掌。在材料学科召开评审会的时候，我提前一周把书寄出去了。后来我得知，当年的学科主任靳达申老师，把我的《魔方及其应用》带到了评审会上，他大谈“晶体学符号和魔方”的妙处，希望评委们能投票支持我的“超塑性的耗散结构模型和金属物理研究”，结果我的申请书被批准了。随后，靳达申老师为程开甲先生组建“集团管理项目”发愁时，因为魔方的印象而把我也拉进了集团的圈子。2007年，我在《中国科学基金》发表了一篇文章，题目是“从事基础研究的三点感想”，公开讲述了我的魔方和基金委金属材料学科(材料学科一处)的缘分(从事基础研究的三点感想.pdf)。

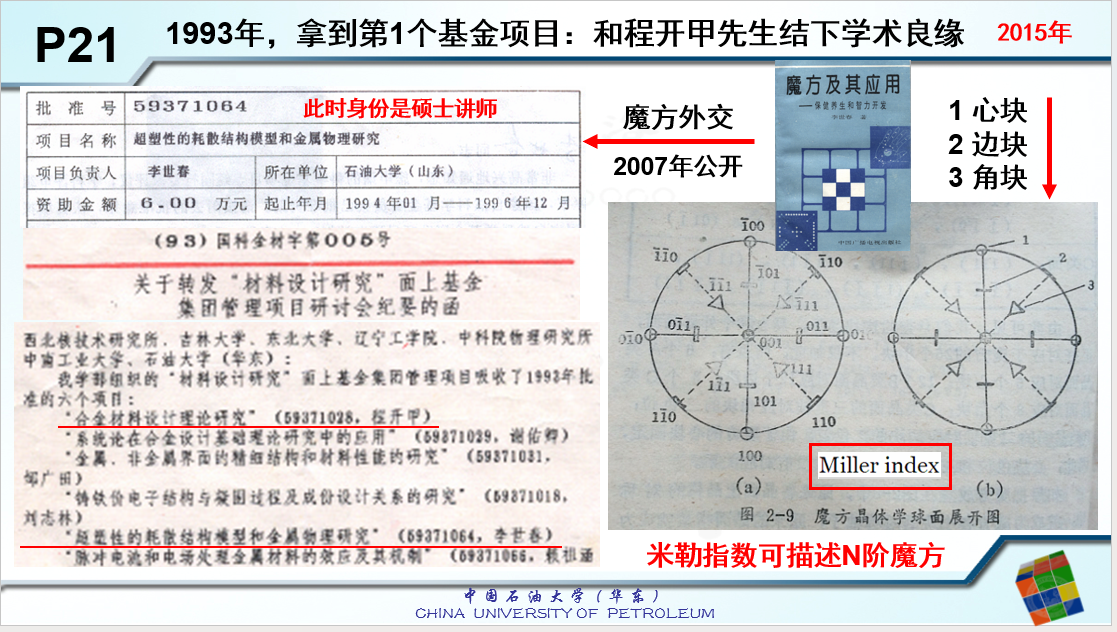
我的项目是研究超塑性的，在当年的申请书里，没有涉及余先生的EET，和材料设计也没有关系。但是金属材料学科(材料科学一处)的靳达申老师，就是因为魔方才把我推荐给程先生的。

身无彩凤双飞翼，心有灵犀一点通。

 这是唐代诗人李商隐的名句，可以描述科学思想的相通和科学灵感的共振。

 1993年12月，在北京钢铁研究总院，国家基金委金属材料学科(材料科学一处)组织召开“材料设计研究”面上基金集团管理项目研讨会，在这次会上我第一次见到了程开甲先生。1993年程先生75岁，当年程先生给我的感觉是“坐如钟、站如松、行如风”，程先生不愧有20多年穿军装的军旅生涯(程先生曾任基地副司令)。

苏东坡说：“遥想公瑾当年，小乔初嫁了，雄姿英发”，距离程先生的军旅生涯，已经60多年过去，距离我和程先生首次见面，也已经32年过去了。

 苏东坡又说：“人生如梦，一尊还酹江月”。如果怀揣梦想，人生就不是一个梦，而是一个美丽而动听的故事。

 在这次研讨会上，程先生作了关于“TFD模型及其应用”的报告，报告的重点内容是关于TFD电子密度，像原子序数Z、原子半径r和电子密度n等参数，都反复出现在我当年的笔记本里。

 对于晶体，原子半径实质上就是点阵常数，因此，我决定用超塑性Zn-5Al合金做X射线衍射实验，试探能否和程先生的TFDC模型产生关联。

 三年之后的1996年，我用Zn-5Al合金样品，做了第一批X射线衍射实验，结果是：Al相晶胞收缩，Zn相晶胞膨胀。在程先生的家里，我给程先生讲述我的实验结果，程先生听后表现出了极大的兴趣，显得特别兴奋，因为我的实验结果正中了程先生TFDC模型的下怀。在这次谈话中，我也很兴奋，因为我触及到了程先生TFDC模型的实质性内核(亮点)。和程先生讨论之后，我根据TFDC模型解释了我的实验结果。

X射线衍射结果表明：对于再结晶态，合金中Al相的晶格收缩，点阵常数比纯Al的小，而Zn相的点阵常数大于纯Zn的。对于超塑变形态，合金中Al相的晶格收缩更为明显，而Zn相的点阵常数仍然大于纯Zn的。

需要强调的是，Zn-5Al是双相合金，能呈现出5000%的延伸率，其主要微观机制是相界滑移，如何控制调节这种机制持续长久，这是另外一个问题。也就是说，Zn-5Al合金存在巨大数量的相界面，也就是Zn原子和Al原子广泛地相互接触。

为了用TFDC电子密度解释这个实验结果，我使用了一个非常简单的“二原子模型”，即只考虑两个原子，一个Al原子和一个Zn原子。我的解释是：

当Al原子和Zn原子接触时，在接触面(相界面) 应该满足量子力学波函数连续的条件，即电子密度相等。由此造成的结果是:电子密度小的原子要收缩半径，以便增大表面的电子密度；而电子密度大的原子要膨胀半径，以便减小表面的电子密度。对于晶体材料，点阵常数的变化就是原子半径的变化。因此，Zn-5Al合金中Al相晶格收缩和Zn相晶格膨胀与电子效应有关。我写成一篇文章，1999年发表在《自然科学进展》，题目是“Zn-5Al合金超塑性的量子效应”。

举例来说，当你把左手放到冰水里，把右手放到热水里，经过一段时间后，你把两手浮出水面合拢，并且把一支温度计置于合拢的两手中间，毫无疑问，温度计只有一个读数。也就是说，左手和右手界面处的温度是连续的，因为温度计只有一个读数。

同样，Zn原子和Al原子接触的界面处，电子密度也只能有一个读数，这就是所谓的电子密度连续，也就是量子力学波函数的连续。

 1996年，我终于实质性地跨进了程先生的“材料设计”集团管理项目。根据X射线衍射实验的结果，我立刻做出了决定，从此以后，对程先生的TFDC模型，我只聚焦在TFDC电子密度，而且要把我的“二原子模型”坚持到底，后来的TFDC相图(TFDC相图.pdf)和维加德定律的原子模型(Empirical atom model of Vegard's law - ScienceDirect)，都采用了“二原子模型”。

 需要说明的是，我的X射线衍射实验都是在清华大学材料中心陶琨实验室做的，陶琨也是分学位委员会主席，我申请博士学位时，很多环节将要和陶琨老师打交道，我提前用X射线衍射实验铺垫了我和陶琨老师的学术关系。实际上，2000年答辩的时候，陶琨老师也是答辩委员会的，他对我的X射线衍射结果充满信心。

 因为我选择只关注TFDC电子密度，自然而然地，我就把触角伸向了余瑞璜先生的EET经验电子理论。

1999年这篇文章的题目里，我把余先生EET经验电子理论称呼为晶体价键理论，把程开甲先生的TFDC模型称呼为晶体电子密度理论，因为我的沟通方法(公式)依赖于晶体结构。TFDC模型和EET比，显然TFDC模型更物理，更接近第一原理，实际上，现代密度泛函理论(DFT)早期就采用TFD近似。

此时我对余瑞璜EET的思考，出现分岔口：一条路是往点群空间群走，一条路是往价电子结构走。

在EET的岔路口，到底应该往哪走？

实际上，对我来说，这个问题的本质就是余瑞璜EET经验电子理论的亮点到底在哪里？

孤帆远影碧空尽，唯见长江天际流。

这是李白的名句，可以描述我当时站在EET岔路口上的感受。我已经下决心要找到余瑞璜EET经验电子理论的亮点，因为我要把以后的精力投注在EET的这个亮点上。

还是这句老话：山不转水转，水不转人转，人不转魔方转，魔方不转点群转。

    待续最后一篇：我和余瑞璜先生的缘分(5)

参考文献：

科学网—退休10年：十载闲云外，心同野鹤轻 - 李世春的博文

科学网—我和余瑞璜先生的缘分(1) - 李世春的博文

科学网—我和余瑞璜先生的缘分(2) - 李世春的博文

科学网—我和余瑞璜先生的缘分(3) - 李世春的博文