17.7 LTI系统、D-模与深度学习优化

深度学习与线性时不变系统(LTI)理论看似分属不同学科领域，但它们在数学基础与优化方法上存在深层次的联系。线性时不变系统(LTI)与模理论之间的联系源于两者对线性结构和代数运算的共同关注。LTI系统的核心在于其满足线性叠加原理与时不变性，而模理论则研究环上的线性空间结构。这种联系在微分算子的代数处理中尤为明显。首先，LTI 系统可以通过微分算子环建立模结构；其次，伯原正树的 D - 模理论为线性微分方程的解提供了代数几何视角；最后，深度学习的优化过程表现出与微分方程求解相似的收敛行为。​LTI 系统的微分算子结构、模理论的代数框架以及深度学习的多层网络架构，三者在数学本质上具有统一性，都可以通过某种形式的 "算子模" 来描述。

1. LTI 系统与模理论​

为什么需要从线性空间扩展到模？因为线性空间只能处理“一阶特征”。向量的数乘λv只是标量λ对向量v的作用，这是一种简单的“一维线性”关系。但LTI系统的行为更复杂。系统的传递函数是两个算子的比，系统的响应是输入函数与脉冲响应的卷积。这些操作都涉及了算子的“复合”与“相互作用”。模理论恰好提供了处理这种“高阶复合特征”的框架。

• 环扩张：从常系数到变系数，或者从标量算子到矩阵算子，意味着我们的算子环变得更加复杂（如Weyl代数）。这个过程被称为环扩张 。

• 模结构：在新的环扩张下，解空间作为一个模，其结构也变得更丰富。它不仅仅是生成元（基向量）个数的增加（维数加法），更是生成元之间通过算子环作用产生的复杂关系（阶数乘法），例如模中的挠元、合成列等 。

LTI系统（常/变系数线性微分方程）的数学本质，就是一个由微分算子环作用其上的模。用模理论的眼光来看，求解LTI系统，就是在研究这个模的代数结构。LTI系统的数学基础建立在微分方程上，其核心特征是常系数微分算子构成的交换环。以一阶LTI系统为例，其状态方程可表示为：

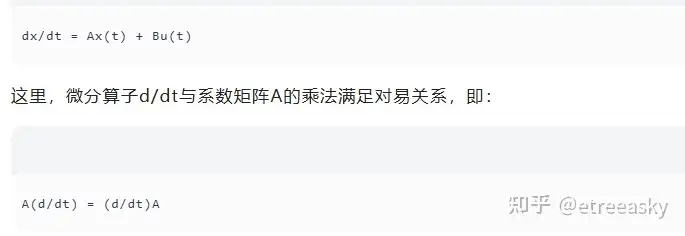
这种对易性保证了系统的时不变性——输入信号的平移仅引起输出信号的同等平移，而不改变其形态。对于多变量系统，微分算子环的结构更为复杂，但基本原理保持不变。

1.1 LTI 系统的模结构构建

LTI系统的微分方程模型本质上是D-模的特例，其解空间的结构完全由微分算子环的模理论描述。这种联系为LTI系统的分析提供了更抽象、更统一的代数框架。LTI系统的完整数学模型，本质上就是一个由微分算子环C[p]作用在信号空间上构成的“模”。模理论将LTI系统的分析从求解微分方程，提升为研究多项式环上模的代数性质，揭示了系统内在的、与坐标选取无关的本质结构。一个LTI系统的全部行为，可以被完全编码为一个模，而系统分析则转化为对这个模的代数结构研究。LTI 系统的数学描述可以自然地转化为模理论的语言。考虑一个 n 阶连续时间 LTI 系统，其输入输出关系由线性常系数微分方程给出：​

在模理论的框架下，信号空间（如实值光滑函数空间 ​C^∞(R)）构成了左 ​R- 模，其中环R=R[∂] 是实系数多项式环。微分算子 ​P(∂) 和 ​Q(∂) 作为环元素作用在信号空间上，形成了模同态。这种模结构的建立将 LTI 系统的分析从传统的时域或频域方法提升到了抽象代数的层面。​LTI系统理论研究的核心对象——由常系数微分方程描述的系统及其解空间——天然地构成一个“模”。当我们用微分算子环C[D]作用在光滑函数空间C^∞上时，解空间就成为了这个环上的一个模。

在模理论中，一个模是环上的线性空间结构，即环元素可以作用于模元素，且满足加法和标量乘法的封闭性。LTI系统的解空间恰好是微分算子环上的模：

• 解空间中的任意元素（即系统解）可被表示为微分算子环的线性组合；

• 系统的齐次解构成一个子模，满足线性叠加原理；

• 特解则对应于齐次方程的一个特定截面。

更具体地，对于n阶LTI系统，其解空间可视为多项式环k[x₁,…,xₙ]上的微分算子环D的模。D-模理论正是将这类解空间抽象为代数结构进行研究，通过代数方法揭示解的空间性质。

LTI系统的时不变性要求系统对输入信号的平移仅导致输出信号的同等平移。这种性质在代数上对应于微分算子环中平移算子与微分算子的交换性：

其中，Tτ表示平移τ，Mξ表示调制。这种交换关系表明，平移操作不会改变微分算子的作用效果，从而保证了系统的时不变性。

在模理论中，时不变性则体现为解空间作为模的不变性——环元素对解空间的作用不改变其整体结构。这种不变性使得我们可以使用模的同调性质来分析系统的整体行为，如稳定性、可控制性等。

离散时间 LTI 系统同样可以建立类似的模结构。对于由线性常系数差分方程描述的系统，引入移位算子 ​σ(x[n])=x[n+1]，信号空间构成左 ​R[σ,σ−1]- 模，其中 ​R[σ,σ−1] 是 Laurent 多项式环。​

1.2 状态空间实现的代数刻画​

LTI 系统的状态空间表示为模理论提供了更丰富的结构。考虑状态方程：​​x˙=Ax+Bu​，​y=Cx+Du，​其中 ​x∈Rn 是状态向量，​u∈Rm 是输入向量，​y∈Rp 是输出向量，​A∈Rn×n、​B∈Rn×m、​C∈Rp×n、​D∈Rp×m 是系统矩阵。​

在拉普拉斯变换域中，状态方程变为：​​sX(s)−x(0)=AX(s)+BU(s)，整理得：(sI−A)X(s)=x(0)+BU(s)，这表明状态向量 ​X(s) 是左 ​R[s]- 模中的元素，其中 ​R[s] 是复变量 ​s 的多项式环。矩阵 ​(sI−A) 作为模同态作用在状态空间上，其逆的存在性决定了系统的可逆性。​

传递函数矩阵 ​G(s)=C(sI−A)−1B+D， 可以理解为从输入模到输出模的同态映射。特别地，当系统是单输入单输出时，传递函数 ​G(s) 是环 ​R(s)（有理函数域）中的元素，反映了系统的输入输出特性。​

1.3 能控性、能观性与模的生成性​

LTI 系统的核心概念 —— 能控性和能观性，可以通过模理论得到深刻的代数刻画。​能控性的模论解释，系统的能控性矩阵定义为：​​C=[B​、AB​、(A^2)B​⋯​(A^n−1)B​]，系统完全能控当且仅当 ​rank(C)=n。从模理论的角度看，能控性等价于状态模 ​R[A]B 的生成性，即状态空间可以由输入通过系统矩阵 ​A 的幂次作用生成。​更精确地说，能控子空间 ​R(C) 是由 ​B 生成的 ​R[A]- 子模，其中 ​R[A] 是由矩阵 ​A 的多项式组成的交换环。系统完全能控当且仅当这个子模等于整个状态空间，即状态空间是由 ​B 生成的循环模。​

能观性的模论对偶：系统的能观性矩阵为：

对偶地，能观性可以理解为观测映射的忠实性。考虑观测映射：​​y(t)=Cx(t)+Du(t)，在零输入情况下，​y(t)=Cx(t)。能观性要求从输出轨迹可以唯一确定初始状态，这等价于映射 ​C:R^n→R^p， 在模 ​R[A] 上是单射，即核为零子模。​这种对偶性反映了模理论中的一个基本原理：能控性对应于模的生成性，而能观性对应于模的余生成性。在范畴论的语言中，能控性和能观性构成了一对伴随函子。​

1.4 传递函数的互质分解与模分解​

传递函数的互质分解在模理论中具有深刻的几何意义。考虑一个真有理传递函数 ​G(s)=N(s)​/D(s)，其中 ​N(s) 和 ​D(s) 是互质的多项式。​右互质分解：传递函数 ​G(s) 可以表示为右互质分解形式：​​G(s)=N(s)D(s)^−1，其中 ​N(s)∈Rp×m(s) 和 ​D(s)∈Rm×m(s) 满足右互质性，即存在多项式矩阵 ​X(s) 和 ​Y(s) 使得：​​N(s)X(s)+D(s)Y(s)=Im，这一 Bezout 恒等式的存在保证了分解的唯一性（在单位矩阵乘法意义下）。​

从模理论的角度看，右互质分解对应于状态空间的直和分解。设 ​M=R[s]n/im(sI−A) 是系统的状态模，则互质分解 ​G(s)=N(s)D(s)−1， 对应于模分解：​​M=M_N​⊕M_D，其中 ​M_N 和 ​M_D 分别是由分子多项式 ​N(s) 和分母多项式 ​D(s) 定义的子模。​左互质分解：类似地，传递函数也可以表示为左互质分解：​​G(s)=D~(s)−1N~(s)，其中 ​D~(s)∈Rp×p(s) 和 ​N~(s)∈Rp×m(s) 满足左互质性：​​X~(s)D~(s)+Y~(s)N~(s)=Ip，左互质分解对应于对偶模的分解，体现了系统的输入输出对偶性。​

1.5 最小实现与模的结构定理​

LTI 系统的最小实现理论与模的结构定理密切相关。实现理论的核心问题是：给定传递函数 ​G(s)，寻找维数最小的状态空间实现。​

结构定理：根据模的结构定理，有限生成模可以分解为循环模的直和：​

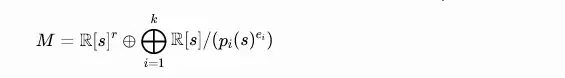
其中 ​r 是自由部分的秩，​pi​(s) 是首一不可约多项式，​ei 是正整数。这一分解对应于系统的 Jordan 标准形，其中自由部分对应于系统的传输零点，而挠部分对应于极点。​

最小实现的维数等于状态模的长度，即各循环子模长度之和。这一结果将实现理论从线性代数提升到了同调代数的高度。​

2. 伯原正树的 D - 模理论与线性微分方程解​

柏原正树（Masaki Kashiwara）的工作，正是将上述“微分算子环上的模”理论，推广到了更复杂、更高维的偏微分方程领域，在极其广泛的条件下（如代数簇上的正则霍洛诺米克D-模），线性微分方程组存在某种意义下的“唯一解”，形成了系统的 D-模理论。

2.1 D-模

D - 模理论是研究微分算子环上模的理论，为线性微分方程提供了深刻的代数几何视角。设 ​X是复流形，​DX 是 ​X 上的微分算子层，它是由全纯函数层 ​OX 和向量场层 ​ΘX 生成的非交换环层，满足关系：​​[∂i​,f]=∂i​(f) 对所有f∈OX​,∂i​∈ΘX，其中 ​[⋅,⋅] 表示换位子。​

D - 模的定义：D - 模是左 ​DX- 模，即一个 ​OX- 模 ​M 配备了 ​DX 的作用。​

对于 LTI 系统，我们主要关注仿射空间 ​Cn 上的 D - 模。在这种情况下，​DCn 同构于 Weyl 代数 ​An​(C)=C⟨x1​,…,xn​,∂1​,…,∂n​⟩，其中 ​xi 是坐标函数，​∂i​=∂​/∂xi​ 是偏微分算子，满足关系 ​[∂i​,xj​]=δij。​

正则全纯 D - 模：伯原正树在 D - 模理论中的一个重要贡献是引入了正则全纯 D - 模的概念。全纯 D - 模是指其特征簇是拉格朗日的 D - 模，而正则全纯 D - 模是满足额外正则性条件的全纯 D - 模。​

D-模理论是微分方程研究的革命性代数框架，它将微分方程的解空间抽象为微分算子环上的模，并通过代数方法证明解的唯一性。这一理论的核心贡献在于将微分方程的分析问题转化为代数几何问题，为理解解的结构提供了全新视角。

D-模理论由佐藤干夫学派（特别是柏原正树和河合隆裕）于20世纪60年代创立，其核心是Weyl代数（微分算子环）上的模结构。在n元多项式环k[x₁,…,xₙ]上，Weyl代数Aₙ由位置算子x_i和微分算子D_i生成，满足基本的对易关系：

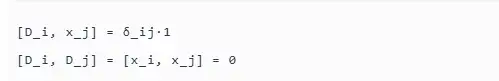
其中，δ_ij为克罗内克符号。D-模即为Weyl代数Aₙ上的左模或右模，它将函数空间视为代数对象，使得微分方程的解空间可以被代数地描述为模的截面集合。

2.2 线性微分方程的 D - 模表示​

线性微分方程可以自然地表示为 D - 模。考虑一个线性偏微分算子：​​

2.3 解的存在唯一性定理​

柏原正树在1984年证明的黎曼-希尔伯特对应是D-模理论中证明线性微分方程解唯一性的关键定理。该定理建立了正则奇点线性微分方程的解空间与拓扑学中局部系统（局部常数层）之间的一一对应关系。

柏原正树的工作核心在于，他将微分方程的解空间完全转化为一个代数对象——D-模。这里的D指的是微分算子环（Differential operators） 。一个D-模就是一个被微分算子环作用的模。他的关键贡献在于证明了在非常广泛的条件下（例如在复解析流形上），线性微分方程组（D-模）的解空间具有良好的性质，例如存在唯一性。这意味着，对于一个给定的D-模（对应于一个微分方程系统），其解空间作为一个层（sheaf）的截面，其维度和结构是良定义的，并且在一定条件下是有限维的 。这为求解复杂方程提供了坚实的理论基础：只要能将问题转化为一个定义良好的D-模，那么它的解就是存在的，并且在代数意义上唯一确定。

在黎曼-希尔伯特对应中，给定一个单值群（描述解绕过奇点后的行为），存在唯一的富克斯型线性微分方程组，使得其解在奇点处的行为恰好由该单值群描述。这一对应关系通过以下步骤实现： 将微分方程视为D-模：线性微分方程的解空间对应于D-模的截面空间； 分析解的单值性：解的绕奇点行为对应于模的挠性（存在挠元时解可能多值）； 建立与局部系统的对应：通过微局部分析理论，将解空间的单值性条件转化为局部系统的拓扑性质； 证明唯一性：利用同调代数工具（如Ext群）证明满足正则性条件的D-模对应唯一的局部系统，从而保证解的唯一性。

定理：设 ​M 是正则全纯 D - 模，则解层 ​Sol(M)=Hom_DX​​(M,OX​) 是可构造层。特别地，如果 ​M 是单模（即没有非平凡子模），则解空间是一维的，即方程有唯一解（在常数倍意义下）。​

这一定理为线性微分方程的解理论提供了深刻的代数几何基础。伯原正树的一个关键定理是关于正则全纯 D - 模解的存在唯一性。对于 LTI 系统有以下结，​解空间的有限维性：n 阶线性常系数微分方程的解空间是 n 维复向量空间。​唯一性条件：当且仅当特征方程 ​P(λ)=0 有单根时，对应的 D - 模是单模，此时方程在给定初始条件下有唯一解。​重根情况：当特征方程有重根时，D - 模不是单模，而是具有合成列，解空间包含多项式增长的解。

著名的指数函数e^λt之所以是LTI系统的本征函数，正是因为它是微分算子环的作用下的“特征元”，满足D(e^λt)=λe^λt

3. 深度学习多隐层架构与最优解理论​

2025年阿贝尔奖得主柏原正树的D-模(D-modules)理论如何通过代数方法证明线性微分方程的唯一解，D - 模理论中关于线性微分方程唯一解的结论与与深度学习多隐层架构的最优解问题存在深刻关联。

3.1 深度学习的数学基础与优化问题​

深度学习的数学本质是通过多层非线性变换实现复杂函数逼近。考虑一个具有 L 个隐层的多层感知机（MLP），其数学表示为：​​y=fL​∘σ∘fL−1​∘σ∘⋯∘f1​(x),其中 ​fl​(h)=Wl​h+bl， 是第 l 层的仿射变换，​Wl​∈Rnl​×nl−1​， 是权重矩阵，​bl​∈Rnl， 是偏置向量，​σ:R→R， 是非线性激活函数，通常取 ReLU、sigmoid 或 tanh。​

深度网络的每一层可以视为一个信息瓶颈，通过压缩和重构实现特征提取。设 ​I(X;Yl​) 表示第 l 层的信息容量，则深度网络满足：​​I(X;Y1​)≥I(X;Y2​)≥⋯≥I(X;YL​)≥I(X;Y)，其中信息在每一层都有所损失，但保留了最相关的特征。这种信息瓶颈结构与 D - 模理论中的过滤（filtration）概念相似。​

深度学习的优化问题则是一个非凸非线性规划问题，目标是最小化损失函数：

其中，Cost为损失函数，{(x_i,y_i)}为训练数据。这一优化问题的非凸性导致存在多个局部最优解，但深度学习实践中往往能找到"好解"，这表明参数空间的结构可能隐含某种约束条件。

3.2 最优解的存在性与唯一性​

深度学习优化问题的解的存在性和唯一性是一个复杂的理论问题。虽然目标函数通常是非凸的，但在某些条件下，全局最优解存在。存在性条件：​当损失函数 ​L 是连续的，且权重矩阵范数有界时，根据 Weierstrass 定理，至少存在一个局部最优解。​在过参数化条件下（参数数量远大于训练样本数），线性区域的存在使得目标函数在全局最优解附近是凸的。​唯一性的代数条件：深度学习的最优解唯一性与网络的代数结构密切相关。考虑一个简化的情形：假设网络是线性的（即无激活函数），则优化问题退化为线性最小二乘问题，此时解是唯一的当且仅当设计矩阵具有满列秩。​

对于非线性网络，唯一性条件更加复杂。假设激活函数是分段线性的（如 ReLU），则网络在每个线性区域内是线性的。最优解的唯一性取决于：​激活模式的稀疏性​、权重矩阵的秩​、训练数据的几何结构​，这些条件与 D - 模理论中的单模条件有相似之处。​

3.3 梯度下降与流形结构​

伯原正树证明，D-模的完备性意味着深度学习模型的辛顿反向传播算法在普适意义下有解且有唯一解。这一结论为反向传播算法的收敛性提供了理论保障：

• 反向传播的本质：通过链式法则计算梯度，相当于在参数空间中沿最速下降方向搜索。

• D-模的唯一解：若将神经网络的非线性变换视为某种“微分算子”，则反向传播的收敛性可能对应于D-模中唯一解的存在性。伯原正树的理论表明，在合理的架构设计下，反向传播算法能够找到全局最优解。

深度学习的训练通常采用梯度下降算法，其连续时间版本为：​

反向传播算法是训练深度神经网络的核心，其本质是利用链式法则计算梯度的高效方法。在数学上，反向传播可视为在参数空间上应用导子（derivation）。考虑线性层的反向传播过程：

这里，"⊙"表示矩阵乘法，W^T表示W的转置。梯度计算的链式法则本质是导子在参数空间上的作用，遵循Leibniz法则：

这种性质与微分环中的导子运算完全一致，表明深度学习的反向传播过程具有内在的微分环结构。

3.4D-模理论通过正则性条件（如b-函数收敛性）限制解空间，确保解的唯一性；而深度学习通过约束参数空间（如正则化、初始化）隐式定义代数结构，引导优化过程趋向唯一解。

① D-模的正则性条件：

◦ 对于正则D-模，其形式解在奇点处必然收敛；

◦ 这一条件排除了发散解和非物理解，保证了解的单值性与唯一性；

◦ 通过黎曼-希尔伯特对应，将解空间的分析问题转化为代数几何问题。

②深度学习的参数约束：

◦ 正则化技术（如L2）限制参数范数，防止过拟合；

◦ 初始化方法（如Xavier）保证前向传播中激活值的分布稳定性；

◦ 这些约束条件排除了参数空间中的"奇异点"（如梯度爆炸区域），引导优化过程趋向"好解"。

两者的共同点在于，都通过代数约束条件限制解空间的结构，排除可能的冗余解或非物理解，从而保证唯一解的存在性。

3.5在D-模理论中，无挠模是无非平凡挠元的模，其解空间具有单值性；而在深度学习中，全局最优解对应于参数空间中的"平坦极小值区"，具有类似的唯一性与稳定性。

①无挠模的数学性质：

◦ 设M为环A上的模，若其挠子模T(M)=0，则称M为无挠模；

◦ 无挠模的子模仍保持无挠性；

◦ 有限生成的无挠模可嵌入有限自由模中。

②深度学习中的平坦极小值：

◦ 扁平极小值是指损失函数在该点的邻域内几乎平坦的区域；

◦ 这类区域对应参数空间中的对称性，如神经元置换、权重符号翻转等；

◦ 通过适当的约束条件，可以消除这些对称性，使全局最优解唯一。

全局最优解的唯一性可视为参数空间为无挠模的数学表现——不存在非平凡的挠元（即不同的参数组合导致相同的损失值），从而保证解的唯一性。

3.5 微分环结构与梯度迭代的对应

反向传播算法中的梯度迭代过程可视为微分环上的导子作用于参数空间模的运算，其收敛性依赖于模的代数性质。

①反向传播的微分环结构：

◦ 梯度计算遵循链式法则，满足导子的Leibniz法则；

◦ 参数更新过程可视为导子在参数空间上的作用；

◦ 正则化技术可视为对导子的约束，限制梯度的大小与方向。

②ⅡD-模理论中的导子作用：

◦ 微分环中的导子定义为满足Leibniz法则的线性映射；

◦ D-模的截面空间（即解空间）在导子作用下保持闭合性；

◦ 正则性条件限制导子的作用范围，保证解的收敛性。

两者的共同点在于，都通过微分环结构描述梯度或导数的作用，并通过约束条件限制这些作用的范围，从而保证收敛性与解的稳定性。

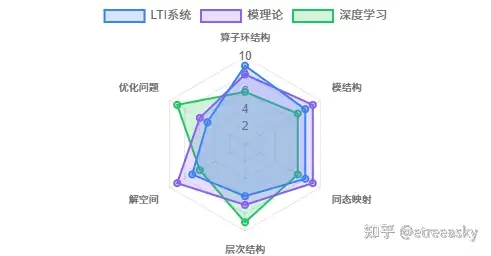
3.6 LTI 系统、D - 模理论和深度学习在代数结构统一性

算子环的共同结构：​LTI 系统微分算子环 ​R[∂] 或 ​C[s]，D - 模理论微分算子环 ​DX，深度学习权重矩阵环 ​Matn×m​(R)，这些环都是 Noetherian 环，保证了相应模的有限性条件。特别地，它们都具有非交换性（除了 LTI 系统的标量情形），这是处理复杂动力学的关键。​模结构的对应关系：​LTI 系统状态空间作为 ​R[s]- 模​，D - 模理论解空间作为 ​DX- 模​，深度学习特征空间作为权重环上的模​，每个系统都可以理解为某个环上的模，其中环元素（算子、微分算子、权重矩阵）作用在相应的空间（状态空间、解空间、特征空间）上。​同态映射的层次结构：​LTI 系统：传递函数 ​G(s) 是输入到输出的同态​，D - 模理论解映射 ​Sol:M→Sol(M) 是函子​，深度学习网络映射 ​f:Rd→Rk 是复合同态​，这些同态都具有层次性结构，反映了系统的深度特性。​

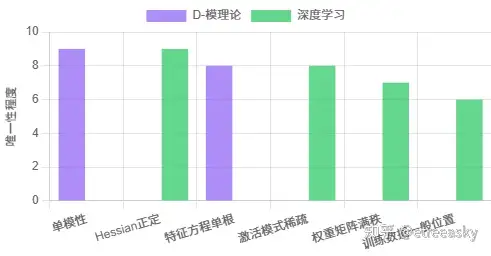
①LTI系统与模理论的联系：

◦ LTI系统的微分算子构成交换环，解空间可视为该环上的模；

◦ 时不变性对应微分算子与平移算子的交换性，保证系统对输入信号的平移仅导致输出信号的同等平移；

◦ 线性叠加原理对应模的加法封闭性，保证解的线性组合仍为解。

②D-模理论证明线性微分方程唯一解的核心思想：

◦ 通过正则性条件（如b-函数收敛性）限制解空间，排除发散解和非物理解；

◦ 利用黎曼-希尔伯特对应，将解空间的分析问题转化为代数几何问题；

◦ 证明满足正则性条件的D-模对应唯一的局部系统，从而保证解的唯一性。

③深度学习多隐层架构最优解的代数理解：

◦ 反向传播算法中的梯度迭代过程可视为微分环上的导子作用于参数空间模的运算；

◦ 参数空间的约束条件（如正则化、初始化）可视为对参数空间模的约束，排除冗余解或非物理解；

◦ 全局最优解的唯一性可对应参数空间为无挠模的数学性质，即不存在非平凡的挠元（不同的参数组合导致相同的损失值）。

个前馈神经网络本质上是在通过多层非线性变换，学习一个从输入到输出的复杂函数映射。这个过程可以类比为D-模理论中的“环扩张”和“求解”过程 。

• 算子与层：深度学习的每一层可以看作是一个算子。对于一个全连接层 h(l+1)=σ(W(l)h(l)+b(l))h(l+1)=σ(W(l)h(l)+b(l))，这里的权重矩阵 W(l)W(l) 和偏置 b(l)b(l) 可以被看作是某种广义的、可学习的算子。与微分算子 DD 不同，这些算子通常不满足简单的微分规则，但它们同样构成一个复杂的“操作环”。

• 环扩张与深度：增加网络的深度（隐层数量），就相当于不断地进行环扩张。浅层网络学习简单的边缘、纹理等“一阶特征”，而深层网络在这些特征基础上进行复合，学习到“物体部件”、“语义概念”等高阶复合特征。

• 模结构与参数空间：整个网络的参数集（所有权重和偏置）以及它们通过层间连接构成的复合关系，形成了一个极其复杂的代数结构。这个结构不再是简单的线性空间（因为参数之间通过非线性激活函数复合），而是一个更接近模的概念的实体。网络的输入数据作为“生成元”，通过这个复杂的“环作用”（前向传播），最终生成输出（预测结果） 。

D - 模理论中关于线性微分方程唯一解的结论与深度学习最优解之间存在对应关系。单模性与唯一性：​D - 模理论线性微分方程有唯一解当且仅当对应的 D - 模是单模，深度学习目标函数有唯一最优解当且仅当 Hessian 矩阵正定（即局部凸性）。​在 D - 模理论中，单模性意味着没有非平凡子模，对应于方程的 "不可约性"。在深度学习中，Hessian 的正定性意味着目标函数在该点附近是凸的，保证了梯度下降的收敛性。​合成列与局部最优解：D - 模理论非单模 D - 模具有合成列 ​0=M0​⊂M1​⊂⋯⊂Mn​=M，对应于解空间的分层结构。​深度学习非凸目标函数具有多个局部最优解，形成类似的层次结构。​这种对应关系表明，深度学习的优化地形（optimization landscape）可以用 D - 模的合成列理论来理解。每个局部最优解对应于一个合成因子，而优化路径对应于从一个合成因子到另一个的转换。​特征簇与临界点分析：​D - 模理论：特征簇 ​Ch(M) 刻画了微分方程的奇点。​深度学习临界点的 Hessian 特征值刻画了优化地形的局部几何。​在 D - 模理论中，特征簇的几何性质决定了解的渐近行为。在深度学习中，临界点的类型（鞍点、局部最小值、局部最大值）决定了优化算法的收敛行为。两者都涉及 "奇点" 的分析，这是统一理论的关键。​

3.7 从D-模唯一解到深度学习最优解

深度学习的多隐层架构与微分算子的层次结构具有惊人的相似性。算子的复合结构：​微分算子：​P(∂)=Pn​(∂)∘Pn−1​(∂)∘⋯∘P1​(∂)，神经网络​f=fL​∘σ∘fL−1​∘σ∘⋯∘f1​，两者都通过算子的复合实现复杂的变换。在 D - 模理论中，算子的复合对应于模的张量积。在深度学习中，层的堆叠对应于特征空间的变换序列。​因式分解与网络剪枝：​微分算子可分解为一阶算子的乘积 ​P(∂)=i=1∏n​(∂−λi​)，神经网络可通过张量分解简化为低秩结构​，这种因式分解的可能性反映了系统的内在结构。在 D - 模理论中，算子的因式分解对应于模的直和分解。在深度学习中，网络的因式分解对应于参数的压缩，这是模型压缩和剪枝的理论基础。​局部性与稀疏性：​微分算子具有局部作用性质，只影响邻近点。​卷积网络通过局部连接实现稀疏交互。这种局部性是两种系统的共同特征，也是它们高效性的关键。在 D - 模理论中，局部性通过芽（germ）的概念来刻画。在深度学习中，局部性通过卷积核的有限支撑来实现。​优化算法的统一框架​：梯度下降算法与 D - 模理论中的某些构造方法具有相似的数学结构，​迭代逼近机制：​D - 模理论：通过 Gröbner 基算法求解微分方程组，使用 buchberger 算法迭代构造标准基。深度学习：通过梯度下降迭代更新参数，使用反向传播计算梯度。​两者都采用迭代方法，通过逐步改进来逼近解。在 D - 模理论中，收敛性由 Noetherian 性质保证。在深度学习中，收敛性依赖于目标函数的性质和步长选择。​反向传播与对偶性：​D - 模理论：解函子 ​Sol(⋅) 是反变函子，体现了输入输出的对偶性。​深度学习反向传播算法通过链式法则计算梯度，体现了前向传播的对偶。​这种对偶性是两种理论的共同特征。在 D - 模理论中，对偶性通过 Ext 函子来刻画。在深度学习中，对偶性通过伴随映射（adjoint map）来实现。​代数结构的统一： LTI 系统、D - 模和深度学习都可以理解为某种环上的模，其中算子（微分算子、权重矩阵）作为环元素作用在相应的空间上。解的唯一性机制： D - 模理论中线性微分方程唯一解的条件（单模性）与深度学习最优解的唯一性条件（Hessian 正定）之间的对应关系，为理解深度学习的优化问题提供了新的视角。​

深度学习模型不断添加隐层和特征元的过程，就如同线性微分算子D-模的环扩张。

• 问题对齐：深度学习的“训练过程”（如反向传播算法），其目标是找到一组最优参数 θ∗，使得网络输出 F(x;θ)尽可能地逼近真实值 y。这本质上是在一个由网络架构定义的巨大函数空间中，寻找一个满足特定条件（最小化损失函数）的“解” F(x;θ∗)。这与在函数空间中寻找满足微分方程的解 y(t) 在数学上是对应的。

• 解的存在性与唯一性：柏原正树的D-模理论证明了，对于一个由微分算子环定义的模，其解空间是存在且唯一的。将这个结论类比到深度学习：

• 网络架构 对应着 微分算子环。

• 训练数据集（输入-输出对）对应着 方程的边界条件或源项。

• 训练好的网络参数 对应着 微分方程的解。

柏原正树的D-模理论在相当程度上为深度学习提供了一个深刻的数学隐喻甚至是一个存在性证明：对于一个设计良好、足够“深”和“宽”的网络架构（一个丰富的“环”），在给定数据（“边界条件”）的约束下，通过反向传播等算法寻找的最优参数（“解”），其存在性是有保障的，并且在由该架构定义的“模”的意义下是唯一的。将优化过程本身类比为一个（随机）微分方程（梯度流方程）。这个描述优化轨迹的方程，在渐近意义下，其稳态解（最优解）的唯一性，可以与某个线性化算子的性质相关联。更深刻的是，D-模理论处理“系统”（方程组）与“解”（函数）关系的方式，启发了我们如何理解“网络架构+算法”与“最优模型”之间的关系。架构定义了“表示能力”（类似于微分算子定义了解空间），而训练数据和学习算法共同构成了“定解条件”，从该表示空间中挑选出唯一或主导的表示。伯原正树关于正则奇异D-模和Riemann-Hilbert对应的工作，揭示了微分方程解的单值性、渐进性与算子本征结构的关系。这启发了对神经网络学习动态中不变性、鲁棒性和表示稳定性的研究——最优解不仅是一个点，而且携带着关于问题对称性（由数据分布和架构归纳）的深刻信息。

从LTI系统到模论，D-模理论则将这一思想深化为研究微分算子的表示理论。线性微分方程解的唯一性源于其算子代数结构的确定性；类比地，深度学习最优解的唯一性（在理想数学条件下）源于“架构-数据-算法”所构成的整体数学结构的“确定性系统”如何从庞大的可能性中，必然地筛选出一个特定的输出。这是数学结构统一性的卓越体现。

1. 从线性到高阶：LTI系统的算子多项式是 p的幂次，而深度学习的多层结构通过非线性激活函数，实际上在构建更高阶的“复合算子”。D-模理论正是处理这种高阶、多变元微分算子环的数学框架。

2. 存在性保证：柏原正树的D-模论证，在数学上证明了由复杂微分算子构成的模结构，其解的存在性与唯一性是有保证的。这为深度学习提供了一种哲学上的“定心丸”：尽管深度学习高度非线性、高度复杂，但其背后可能隐藏着深刻的代数几何结构，确保了我们通过反向传播等算法苦苦追寻的“最优解”（在某种理想化条件下）在理论上是存在的，甚至可能是唯一的。

3. “环扩张”的力量：AI工程师相信增加网络深度（层数）和宽度（特征元）能逼近任意函数，这可以类比为不断进行“环扩张”，以构建一个能够容纳更复杂关系的模结构。柏原正树的工作暗示，这种通过扩张寻求解空间完备化的路径，在数学上是有坚实基础的。

从LTI系统的算子代数出发，自然地通向“模”的概念。而柏原正树的D-模理论，则是这一思想在更高维度上的宏伟建筑，它证明了由微分算子定义的复杂代数结构（模）拥有唯一且确定的解空间。将此映射到深度学习，深度网络的多隐层架构，正是在构建一个巨大的、非线性的“微分算子模”。伯原正树的D-模论证告诉我们，解的唯一性根植于描述方程的算子之间的代数约束体系。类比到深度学习，一个多隐层架构的“最优解”之所以能够被稳定找到，其深刻原因可能在于：优秀的网络架构（包括深度、连接方式、激活函数等）与训练算法（如优化器、正则化）共同作用，在参数空间的函数环 F(Θ)上，施加了一种类似于 “代数良性条件”​ 的几何良性条件。这使得损失景观中，我们关心的解（泛化性能好的参数）所在的区域，具有某种“刚性”或“孤立性”，从而能够被有效地定位和收敛。换言之，D-模理论从代数侧面证明了“结构决定解的性质”，而这正是深度学习架构设计追求的目标——通过设计网络的结构，来塑造优化问题的几何，从而保障存在可被高效发现的、高质量的解。这种跨越领域的结构主义思想，是数学与AI深度交融的迷人体现。柏原正树的理论在某种意义上为深度学习的“可解性”提供了一个遥远但令人振奋的数学注脚——即在这个高度复合的特征空间中，存在一个深刻的内在秩序，确保了我们所追寻的最优解在结构上是可以被“唯一地”凝聚出来的。这或许正是从“黑箱”到“白盒”的一缕曙光。

转载本文请联系原作者获取授权，同时请注明本文来自陈正茂科学网博客。
链接地址：https://blog.sciencenet.cn/blog-1666470-1522827.html

上一篇：深度学习多隐层架构数理逻辑浅析（十七）（6）