17.5 螺旋结构

一、 "螺旋"LTI系统的稳定性

我们从神十航天员太空授课视频中看到，航天员在太空演示陀螺仪转动实验。首先静止不旋转的陀螺放在这儿，给它一个干扰力，它会翻滚着乱动，它的轴向显然发生了很大的改变。但是，奇特的是，如果将旋转的陀螺放到同样的位置，给它同样一个干扰力，这次它却不翻滚了，而是晃动着顽强地相对平稳向前走。这时，旋转着的陀螺仪的轴向基本上没有发生改变。这个试验显示：旋转⊗平移=稳定。

螺旋模式的“旋转”⊗“平移”复合的螺旋结构往往意味着稳定系统。比如，在枪管内腔增加来复线，子弹出镗自带旋转，射击精准稳定，抗干扰强。

涡旋动力学，流体中涡旋的螺旋破裂现象，其线性稳定性分析可归约为螺旋模态的指数增长率判定。

无论是宏观星系还是微观湍流，螺旋模式提供了跨尺度的LTI描述框架。因为"螺旋模式"LTI系统的稳定性，所以螺旋结构是所有星系的基本结构：

柯西-黎曼方程描述的解析函数特性与LTI系统的因果性和稳定性条件高度一致。因果系统的频率响应满足希尔伯特变换关系，在复平面上形成特定的螺旋对称性。

系统稳定当且仅当所有极点位于复平面左半部分，这在几何上表现为螺旋向原点收敛。LTI系统的稳定性、振荡性直接对应螺旋特性——极点实部σ<0对应收敛螺旋（稳定）、σ=0对应等幅螺旋（临界稳定，即圆）、σ>0对应发散螺旋（不稳定）；极点虚部ω对应螺旋旋转频率，即系统振荡频率。

【稳定性判据】螺旋数学结构直接解释了量子波函数演化、流体涡旋、经济周期等螺旋现象的线性稳定性分析基础。当LTI系统的状态矩阵具有复特征值 λ = α ± jβ 时，其状态轨迹在相空间中精确地构成对数螺旋：

{r} = α r ，{θ} = β

⇒

r(t) = r_0 e^{α t}, θ(t) = θ_0 + β t

稳定性判据为，α<0时螺旋收敛（稳定焦点），α>0时发散（不稳定焦点），α=0时为闭合圆（中心）

二、 "螺旋"LTI系统的普适性

"螺旋"作为LTI系统的特例，呈现LTI系统的特征属性。

螺旋不仅是LTI系统的解的形式，更是其几何指纹。从弥散方程到薛定谔方程，从控制论到深度学习（ResNet的离散动力系统本质），螺旋结构揭示了线性规则在时不变约束下必然涌现的普适模式。

在飞行器、机器人等物理系统建模中， "螺旋模式"(Spiral Mode) 是LTI系统分析的标准术语，指代由复极点产生的特定运动模态。横航向动力学，飞机的荷兰滚(Dutch Roll)和螺旋模式是LTI状态矩阵的本征运动，特征向量决定各状态的参与比例。

在图像处理中，LTI系统理论扩展为空间不变系统，其频率响应在二维频域中形成螺旋状滤波器。 圆锥螺旋线的数学描述（如 x=lsinα·φcosφ）与LTI系统的多维频率响应存在数学同构。在这个意义上，螺旋是这些物理系统内在的、自然的运动模式，而线性时不变系统理论则为描述和预测这些模式提供了完美的框架。

许多物理系统（如电路、弹簧质量系统、声学系统）在小信号近似下都可以建模为线性时不变系统。这些系统的固有振动模式，正是表现为螺旋（或正弦/余弦）运动。 例如，一个阻尼震荡系统的响应，就是一个幅度指数衰减的螺旋（复指数）。系统的参数（阻尼、固有频率）直接决定了这个螺旋的收敛速率和旋转速度。

保角映射理论解释了LTI系统如何在复平面上"扭曲"输入信号的频率分布，形成特定的螺旋轨迹。世界的振动（螺旋）通过线性时不变系统（滤波器）的塑造，最终呈现出我们听到的声音、看到的图像和测量到的各种信号。

LTI系统对复指数输入信号 x(t) = e^{ω t} 的响应为 y(t) = H(ω)e^{ω t}， 其中 H(ω) 是系统频率响应，可表示为：H(ω) = |H(ω)|e^{∠ H(ω)}， 当频率ω变化时，H(ω) 在复平面上的轨迹形成螺旋曲线，其旋转速度与系统相位特性相关，频率响应了螺旋特性。

线性时不变系统不会“创造”新的螺旋频率，它只是像一名调音师，对不同频率的螺旋成分（e^(jωt)）进行不同程度的缩放（由 |H(jω)| 决定） 和旋转（由 ∠H(jω) 决定）。

当系统具有线性相位特性时，θ(ω) 与 ω 成线性关系，对应阿基米德螺旋；当具有对数相位特性时，对应对数螺旋。系统带宽决定了螺旋的"紧密度"，带宽越宽，螺旋旋转越快。

【斐波那契数列】自然界螺旋的离散表达，可精确表征为一个因果LTI系统的脉冲响应：

差分方程 y[n] = y[n-1] + y[n-2] + x[n]

系统函数 H(z) = frac{z}{z^2 - z - 1}

其极点恰为 p_1 = φ（黄金比例） 和 p_2 = -φ^{-1}。当系统受单位脉冲激励时，输出正是斐波那契数列，其连续项比值收敛于φ，从而在连续极限下生成黄金螺旋。这揭示了自然界的螺旋结构（星系、贝壳、飓风）本质上是特定LTI系统（自相似增长律）的时域响应，黄金比例是系统极点的几何表现。

三、 "螺旋"LTI系统的完备性

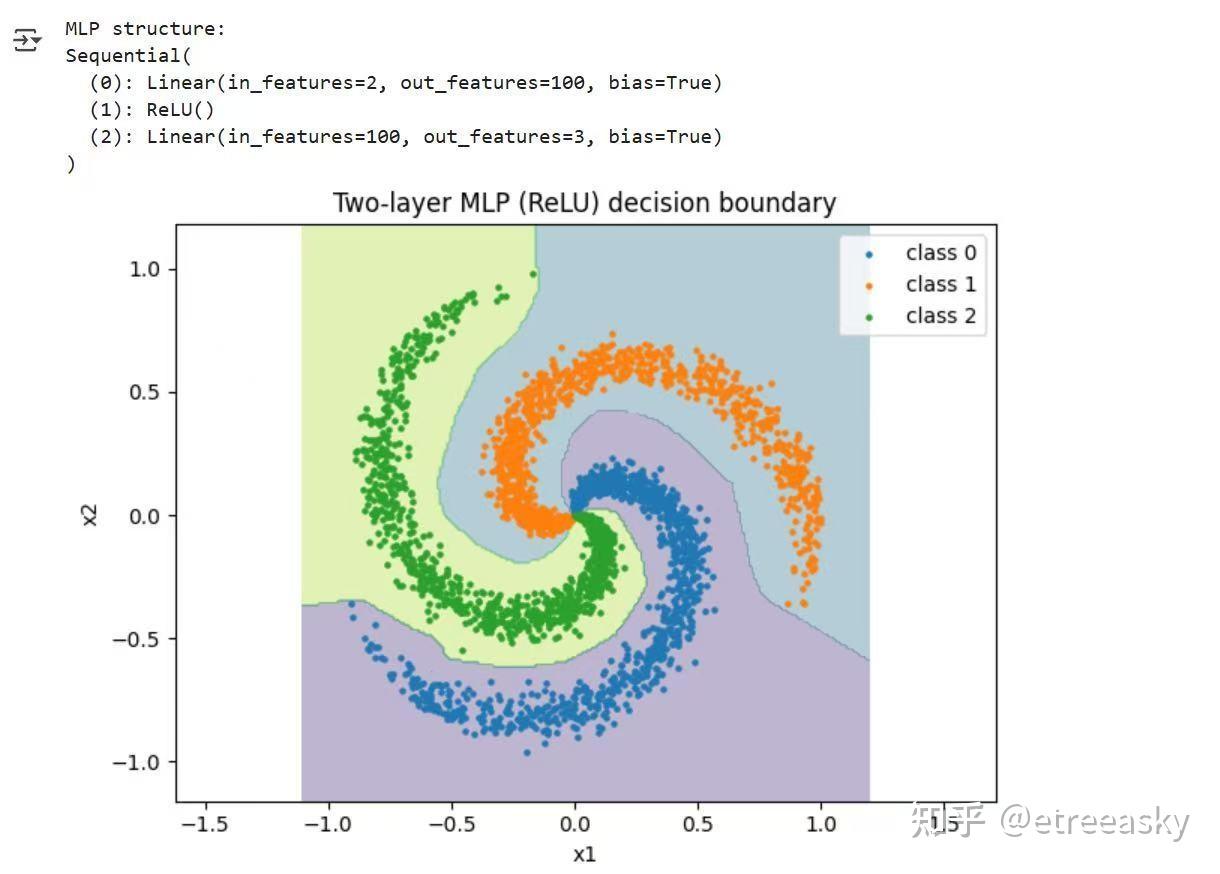
玩过TensorFLOW的同学都知道， 旋转圆圈容易聚类匹配(表征旋转圆圈也不难)、平移方块容易聚类分割(表征平移运动不难)，但是对螺旋结构却相对难以表征分割（深不可测）。因为螺旋结构是“平移和旋转的二阶复合体”（甚至可以看出三阶复合体：旋转⊗平移⊗缩放=螺旋运动），“原空间平移基矢⊗对偶空间旋转基矢”的高阶复合空间参照系具有完备性。

前面章节我们探索了卷积即联合概率，相当于多重线性映射空间的逻辑‘与’，所以卷积是一种高阶线性特征。我们来探讨卷积和线性时不变系统的珠联璧合。在线性时不变系统中，卷积的优势淋漓尽致充分发挥。

线性系统（包括多重线性结构）我们已经很熟悉了，但是“时不变”是什么意思，似乎总是有一种说不清道不明的若隐若现让人眩晕。 下面，我们从"卷积"的角度来品味“时不变”的内涵。 线性时不变系统的响应不是由单独的x或y变量决定，而是由x与y的差所决定。因此系统不是分别x或y的单独作用，不是x或y的单变量函数，而是关于（x-y）的共同函数。而且，线性时不变系统的核函数h(x,y) 是 (x-y) 的共同函数。【注意：时域的延时相当于频域的相位】

并且，如果系统由卷积得到，则它是时不变的；同时，如果系统是时不变的，则它一定由卷积得到。 即：当且仅当一个系统由卷积得到，它是时不变的。“卷积”和“时不变”有深刻内在关系。首先，卷积算符和时延算符的作用是Abel群，具备乘法交换律； 其次，“卷积”不仅是“线性”的，还是“时不变”的。在线性时不变系统中，线性算符和时延算符的作用是Abel群，满足乘法交换律。

时不变系统的意义，正如字面含义，要点在于“不变量”。一切的随机现象，虽然作为单个‘个体特征’而言随机事件是不确定的，但是作为‘整体特征’属性的概率分布(数学期望）却是不变的。‘个体特征’事件也许偶发，但大量个体汇集的‘整体特征’现象符合大数法则概率稳定。系统的固有特征属性是关键。 在大量个体堆积的试验中，随机非确定的单个‘个体’特征现象虽然不具备确定的可验证性，但是其‘整体’系统固有特征属性的概率特征却是不变的、可验证的、可重复实验的。这就是说，‘个体特征’不稳定的随机系统，可以扩充到完备空间时，从而成为‘整体特征’稳定的时不变系统。 后面，我们还会详细探讨伽罗瓦‘域扩张’形成的高阶张量，其不同层次“不变性”与相应群变换（封闭性、完备性）的深刻内在关系。 只要你愿意，一方面，任何系统都可以分解为线性系统（或者多重线性映射系统），以矩阵（或者高阶张量）表达；另一方面，一切随机系统都可以扩充拼凑成时不变的完备系统，从而能厘清内在简洁规律。这意味着，所有的系统都可以扩充为线性时不变系统，通过卷积定律轻而易举实现高阶逻辑演算。卷积表达多重线性映射，所以当我们利用多层次线性逻辑空间多重复合表达事物时，卷积是当之无愧的利器。卷积是‘联合概率密度’的特殊运算，深度学习多隐层的多重函数复合即‘联合逻辑与’运算。

螺旋与线性时不变（LTI）系统有深刻联系，线性时不变系统的本质，是对“螺旋”进行缩放、旋转、平移操作的系统。LTI系统的线性保叠加、时不变保频率，等价于对“螺旋基”的保结构变换，螺旋是能让LTI系统保持输入输出形态一致性的唯一信号几何形式。LTI系统的“天然适配信号”是复指数螺旋，输入该螺旋信号，输出仅为螺旋幅度缩放+相位偏移，螺旋形态完全保持（线性+时不变性共同决定，普通系统会破坏螺旋结构）。 LTI系统对谐波信号的处理在几何上可视为螺旋操作时频，LTI系统对正弦输入仅产生幅度缩放和相位旋转，这恰是复平面上螺旋向量的乘法运算。 交流电力系统建模中，"螺旋向量"(Spiral Vector)将时变信号映射为旋转相量，使非线性时变系统降维为LTI模型。快速傅里叶变换采用"蛇形/螺旋存储"，递归分解本身即是螺旋分形结构的算法实现。在时最优控制问题中，系统状态向目标收敛的切换曲线被映射为对数螺旋。 仿射变换通过坐标变换，二阶LTI系统的可达集边界变为相似对数螺旋，其旋转中心、缩放因子直接决定最优切换时间。 螺旋结构允许解析计算切换次数和时间，避免数值搜索，计算复杂度从O(N²)降至O(log N)，算法效率较高。螺旋是LTI的"自然语言"，LTI系统的本质是线性叠加+时间平移不变性。螺旋结构恰好同时满足这两个特性，一是线性（螺旋的径向增长和角向旋转可线性分解），二是时不变（螺旋的自相似性r(θ+2π) = k · r(θ)保证时间平移下的形态不变。r(θ+2π) = k · r(θ)是一个简洁而富有张力的方程，它统一了从普通周期到对数螺旋的一族结构，其核心是旋转变换与平移变换的耦合对称性。）

四、"螺旋"旋量生成元虚数i

“原空间平移基矢⊗对偶空间旋转基矢”的高阶复合空间参照系具有完备性。“原空间平移基矢位移r⊗对偶空间旋转基矢频率p”的高阶复合空间参照系具有完备性，exp(ipr)是全体线性时不变系统的公共基，所以线性时不变系统具有完备性。这里频率p、位移r是exp(ipr)中的不可或缺二元变量，那么复数i究竟有什么用呢？老师曾经说过，量子力学的根是ih，有ih的地方就是量子力学，没有ih的不是量子力学，i是量子力学不可或缺的元素。

如果我们仔细看，会发现作为线性时不变系统共同本征基的exp(ipr)函数的怪异：两个变量分别取值连续实数、但其联合空间特征属性却大于连续实数。并且，更让人丈二和尚摸不着头脑的是，基元函数exp(ipr）为什么需要个虚头巴脑的虚数来撑门面呢？虚数i在这个函数里到底是何特殊含义？ 如果去掉虚数i的exp(pr)函数，又会有什么不同呢？

数学家发现，虽然带虚数i的exp(ipr)是线性时不变系统的共同本征函数系，但奇怪的不带虚数i的exp(pr)却并不是所有线性时不变系统的共同本征函数系。这个特别的现象，隐含着一个不为人注意的秘密：作为特征函数，exp(ipr)比exp(pr)、sin、cos更基础。虽然很多书籍习惯把exp(ipr)看作exp(pr)的复数形式、把exp(ipr)看作sin和cos的组合形式。但由于exp(ipr)更加基础，其实我们更应该把sin、cos看作exp(ipr)的组合形式才合理。物理学家发现虚数i在量子力学并非可有可无，离开了虚数i量子力学几乎所有的重要方程都无法表达。

同样，在信息光学领域，虽然冲激函数δ(r-p)、复指数函数exp(ipr)、余弦函数cos(x)都称为基元函数。但是余弦函数的基元函数称号，只是相对于某一类特殊线性时不变系统（其脉冲响应是实函数）而言的。这个不含虚数i的余弦函数cos(x)，虽然是‘特殊’线性时不变系统本证函数，却并非‘任意’线性时不变系统的本证函数。换句话说，尽管都称为基元函数，但余弦函数cos(x)与复指数函数exp(ipr）相比是狭隘的，不具备普遍意义。很明显，虚数i的意义举足轻重。

那么这个虚值i到底什么含义呢？不知道是不是汉语翻译的误导，当年学习复变函数初见虚数时，童靴们本能的反感它，下意识里虚数就意味虚无缥缈，犹如玄学，而无暇领略它那万丈光芒。 本质上，虚数i代表了单位周期结构最基本形式： 如果我们计算i、i平方、i三次方、i四次方、i五次方、i六次方、i七次方、i八次方......，结果是i、-1、-i、1、i、-1、-i、1............ 即，i、-1、-i、1的这四个元素反复循环。 显而易见，i它是逻辑循环的基本构件，i代表了旋量生成元，是高阶张量不可或缺的因素。

深入理解，为什么非得引入虚数，系统才得以完备呢？

高等代数【基本定理】可以一窥究竟：[任何一元n次复系数多项式方程，在复数域内有且只有n个根（重根按重数计算）。] 与这个定理对应的是，n次方程在实数域不一定有n个根。换句话说，只有在复数域中方程解才是完备的，而实数域则不完备。（注意,因为复数域是代数闭域,不存在无法求解的问题。复数域上的一元多项式环是唯一分解的整环UFD,可以推出特征值特征向量的存在性。）

五、 复特征值生成对数螺旋的核心数学同构

另一方面，稳定系统往往就是“线性时不变系统”，而exp(ipr)恰恰是所有线性时不变系统的共同本证函数。特征函数/基函数 对特征函数进行操作的算子，自然存在的基本模式 对螺旋进行缩放和相位旋转。 事实上，复指数函数exp(ipr)本身就是一种螺旋结构。线性时不变系统是一个“螺旋处理器”，它天生就“认识”螺旋（复指数），并将其作为分析一切信号的基石。

“螺旋” (复指数 e^(st)) 是线性时不变系统。这里的“螺旋”不是指三维空间的螺旋线，而是指复指数函数所描述的，在复平面上的螺旋轨迹。 在复平面上，系统频率响应 H(ω) 可用极坐标表示为：H(ω) = r(ω)e^{jθ(ω)}。这与螺旋线的极坐标方程 r(θ) = a + bθ 具有数学同构性。

复频域中的螺旋表示为复指数螺旋在LTI冲激响应，源于复指数信号e^(st)是LTI系统的特征函数，而e^(st)=e^(σt)e^(jωt)在复平面的几何轨迹就是螺旋，σ决定螺旋收敛/发散、ω决定旋转角速度。

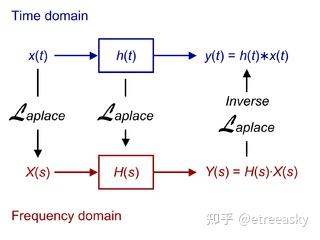
线性时不变系统的核心分析工具是傅里叶变换和拉普拉斯变换。而这两种变换的基函数（或者说“原子”）正是复指数函数：e^(st)， 其中 s = σ + jω（j是虚数单位）。这个函数描述了一个螺旋， e^(jωt) 表示一个在复平面上以角速度 ω 做纯旋转的单位圆， e^(σt) 表示一个指数增长(σ>0)或衰减(σ<0) 的标量， 二者结合 e^(st) = e^(σt) * e^(jωt)， 描述的就是一个幅度随时间指数变化、同时以恒定角速度旋转的螺旋线。σ 控制螺旋是发散的(σ>0)、收敛的(σ<0)还是稳定的(σ=0，即纯圆)。

拉普拉斯变换与螺旋结构息息相关。线性时不变系统的特性可通过拉普拉斯变换完整描述，其变换域为复平面（s平面）。 拉普拉斯变换的复变量表示为：s = σ + jω，其中σ为实部（衰减因子），ω为虚部（角频率）。 当系统响应在复平面上绘制时，频率响应轨迹常呈现螺旋形态，特别是当系统具有复数极点时。拉普拉斯变换本质是将任意信号分解为无数不同参数的螺旋分量，LTI系统的s域传递函数H(s)，就是对每个螺旋分量的增益-相位调制规则。

在更抽象的线性代数视角下，线性时不变系统可以看作一个线性算子。 螺旋 (e^(st)) 是该算子的“特征向量”。 传递函数值 H(s) 是对应的“特征值”。 这个关系 Output = H(s) * Input， 完美符合特征值方程 A*v = λ*v。因此，分析线性时不变系统，本质上就是在分析这个算子如何作用于不同频率的“螺旋”特征向量上。

在时频分析中，短时傅里叶变换的核函数在时频平面上形成螺旋形窗函数。小波变换的某些基函数（如Morlet小波）在复平面上呈现螺旋结构，与LTI系统的特征函数高度相关。对于线性时不变系统，复指数函数是其“特征函数”。这意味着，如果你输入一个螺旋（复指数信号），系统输出的将是同一个频率的螺旋，只是幅度和相位发生了变化。若输入 x(t) = e^(st)， 则输出 y(t) = H(s) * e^(st)。 其中 H(s) 是一个复数，称为系统的传递函数。傅里叶/拉普拉斯变换的基， 通过传递函数 H(s) 在频域表征。系统的固有振动模式描述系统如何响应这些模式。

【LTI系统频率响应不变性定理】线性时不变系统的核函数h（或传递函数H），体现了系统的不变的固有属性：

若L是线性时不变系统，v是输入，w是输出

即 w=Lv

有 w(x)=h(x)*v(x) ，即w可以表达成h和v的卷积

上式傅里叶变换记为:　　W(s)=H(s)V(s)

证明得到，H(s) 是一个永恒不变的常量。

转载本文请联系原作者获取授权，同时请注明本文来自陈正茂科学网博客。
链接地址：https://blog.sciencenet.cn/blog-1666470-1521537.html

上一篇：深度学习多隐层架构数理逻辑浅析（十七）（4）
下一篇：深度学习多隐层架构数理逻辑浅析（十七）（6）