博文
《测量误差及其不确定性》序言
|
《测量误差及其不确定性》全文本地下载: ![]() 测量误差及其不确定性.pdf
测量误差及其不确定性.pdf
序
人们几乎都不相信传统经典测量误差理论是个错误的理论,甚至很多人认为它完美无瑕,并引以为傲。但是,我的研究表明,传统测量误差理论实际是个错误的理论,错误的根源在于对基本数学概念的错误理解,以致于其自身的概念逻辑根本不能自洽。
现在看起来几乎就是个小儿科的数学问题了。以武汉大学的测绘专业教科书《误差理论与测量平差基础》中的例3-1为例,把等式d=23.4代入到等式σd=0.2之中就得到了数学悖论式σ23.4=0.2。仅凭这一点,就能得到以下几个结论:
1、传统测量理论的测量结果表达式的实际数学含义是,一个常数值的标准偏差不是0。
2、传统测量理论的测量结果表达式违反了最基本数学概念σ2 (C)=0。
3、传统测量理论中重复测得值的发散性概念解释歪曲了其数学表达式的本义,是偷换出来的测量学概念,换言之,它本来就是一个不存在的概念。
4、传统测量理论的整个概念体系都是由偷换的概念派生出来的,实际是无源之水、无本之木。
可以看到,人们一直对这种数学悖论表达式σd=0.2熟视无睹,其无外乎二点:要么忘却了等式d=23.4中的“=”号的数学含义,要么认为23.4就是变量。
一边认为测得值是变量,一边又同时说测得值是23.4,这不就是说23.4是变量吗?
但是,误差是测得值与其真值之差,即∆=23.4-XT,这是个很简单的一次函数式。其中,XT是自变量,∆是因变量,23.4是常数值,——这仅仅是个初等数学概念问题!传统测量理论凭什么要把23.4当做变量反而把XT当做常量呢?一个数值23.4凭什么就稀里糊涂地变成了变量呢?这是什么数学概念?这岂能不让数学界瞠目结舌?
这种问题当然不只是武汉大学教科书独有的,全世界都一样。譬如,在国际测量规范《Guide to the Expression of Uncertainty in Measurement(GUM)》的第89页,案例H.3 Calibration of a thermometer给出的最小二乘平差结果的表达式是y1=-0.1712和s(y1)=0.0029,其同样也是给出了数学悖论式:s(-0.1712)=0.0029。同样的问题,凭什么要把常数值-0.1712当做变量?
这时候可能有朋友会说:你说传统测量理论数学概念错误,那人类目前的科技成就是怎么得来的?这些科技成就不都是以测量为基础的吗?诚然,这些科技成就无可非议。但我的回答是,这其中更多来自测量者的经验传授而不是理论本身,因为人们实践中经常违背理论原理而凭经验搞测量。譬如:测量实践中,用于平差的重复观测值都是来自不同测量条件而没有遵守理论中的“相同测量条件”概念,用于精度统计的误差样本也是来自不同测量条件而没有遵守随机误差概念定义中的“相同测量条件”概念,等等。因为这些经验没有上升为理论甚至与理论中的概念背道而驰,以致于传统测量理论实际是在概念上绕来绕去;又因为它似是而非、煞有介事地绕得还象那么一回事,自然很容易迷惑人。
我们还是以武汉大学的测量学教科书《误差理论与测量平差基础》为例,请看其例7-12。它先给出了一个庞大的误差方程:

在这15个独立的方程中,共有24个未知量:9个自变量和15个因变量。从代数的角度看,该方程组显然无解。
但是,教科书借助最小二乘法——通过求二次函数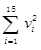 取最小值时的9个自变量的取值,从而给9个自变量赋予了数值,即:
取最小值时的9个自变量的取值,从而给9个自变量赋予了数值,即:

吃惊不?9个自变量都分别被赋予了唯一数值,自变量这下就被绕成数值了。
紧接着,把9个数值代入到原方程就得到15个因变量的数值,一个无解的方程组就这样绕得“有解”了。
被赋予了数值的量当然不是变量,因为它只代表一个数值,而不代表一个数值集合中的所有数值的任何一个。
如果只是绕到这里为止,那倒确实也没什么大碍。相信您也看到,最后混淆一下数值和变量数学概念并不影响最佳测得值的提交,姑且就当作是理论高超“促使”自变量和因变量“演变”成了常数值吧。
但是,它随后又鬼使神差地用贝塞尔公式把15个因变量的取值(仅仅6个多余观测)做了个统计,获得一个标准偏差,而且把这个标准偏差挂到了15个观测值的头上了,美其名曰单位权中误差。再然后,借用协因数传播律“推算出”9个测得值的中误差(标准偏差),即:
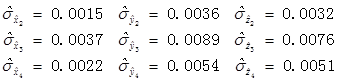
于是,这就如同前边的常数值23.4被框上了标准偏差一样了,这里的15个观测值和最后获得的9个测得值又都分别被框上一个标准偏差——可是,这不就又绕回去了吗?好不容易把变量绕成了常数值,最后却又把常数值重新绕回成了变量(随机变量),甚至把数值的方差是0的基本数学概念也抛弃了。
可见,好在最小二乘法这一基本经验没有问题,好在平差观测值来自不同测量条件的经验没有问题,这种绕来绕去没有给测得值的提交造成颠覆性的问题;但是,这种所谓的中误差(标准偏差)评价显然就是个唬人的东西:其概念定义是相同测量条件下重复测得值的发散性,既和实际做法不一致,也和其数学表达式根本不是一回事。
这确实让人们很难堪,大家引以为傲的传统测量学理论竟然连数值和变量的数学概念都没有搞清楚。特别是那些从事理论教学的同仁,突然发现自己被骗了,而且还骗了自己的学生,当然难以接受。我也很犯难,早年曾以为只是个误差认知方面的哲学性问题,以为做些局部的概念修正可以完事,最后却发现是个数学概念的根子性问题,公式推导不下去了,只能另起炉灶。
正因为如此,传统测量理论只能在概念逻辑上偷来换去、似是而非:一方面是“精度——随机误差——相同测量条件”逻辑,一方面却用不同测量条件的样本做精度统计;一会给变量赋了数值,一会又再绕回去给数值赋方差;一会说系统误差不影响精度,可实际上它有时又影响了精度;一会随机误差影响精度,可实际上它有时又不影响精度;等等。毫无逻辑性,并存在无解的遗留问题。这种概念上的绕来绕去具有很强的迷惑性,因为有些地方绕得还象那么一回事,让人似懂非懂,所以人们一旦被洗脑,就很难再重新回归到数学上的常数和变量概念上来。
自然,回归到纯正的数学概念,把测得值当做常数值,把误差和真值当做变量,那就必然诞生一种全新流派的测量误差理论,必然是一种全新的面貌。而这就是本书即将介绍的内容。
随着多篇论文的发表,谜底已被揭开了多年,但测量学术圈的主流仍然不相信传统经典测量理论是错的,其大抵有几种类型:1、迷信传统理论,迷信学术权威,对任何批判的声音不屑一顾,根本就拒绝阅读这类批判性的文献;2、确实被传统理论洗脑,在传统概念里不能自拔,坚持以传统概念为基准来否定一切批判和创新;3、虽然知道了传统概念逻辑不通,但仍然拒绝承认,死不认账,纯粹基于自身利益考量。
这是我20年来的遭遇,也因为如此,新概念测量理论的研究进展非常艰难。
这故事得追溯到20年前。2000年初,在维修一台日产全站仪时,却发现其存在着一种“弓”字形规律的非原理性的测角误差。但在随后与国家质量技术监督局的专业人士的交流中却面临到一个涉及事件定性的逻辑困扰:这是一种规律误差,属于系统误差而不是随机误差;按照传统测量理论的概念逻辑,系统误差又是不影响精度的,那么仪器仍然属于高精度仪器吗?但我们又都清楚地知道这种误差实际是影响测量精度的——测量理论背离了测量实践,存在逻辑矛盾。
随后又注意到这种误差类别逻辑矛盾问题不仅是个理论问题,而且也给测量实践带来了困扰。譬如,在我国光电测距仪计量检定规程JJG703-1990和JJG703-2003中,测距仪加乘常数误差都没有规定限差。于是我在2004年全国测绘仪器学术年会(成都)上发表了一篇评论《论测距仪加乘常数检验的地位和作用》,其基本论点是计量检定规程应该给测距仪加乘常数误差规定限差。但这一论文在专家委员会的评议中遭到了诸多测绘界学者的反对,甚至有专家明确表达“叶老师犯了概念错误”,理由是加乘常数是可以改正的,不影响精度。自然难以接受这种评价,随后这一论文发表于《中国计量》杂志。
2008年,在海南三亚,全国几何量长度计量技术委员会对JJG703光电测距仪检定规程进行再版评审,测距仪加乘常数误差的限差标准议题正式摆到了计量技术委员会的桌面,二派观点仍然尖锐对立。计量派认为,测距仪加乘常数误差是系统误差,是仪器的准确度评价指标,应该规定限差;测绘派则认为,系统误差是可以改正的,大误差和小误差都是一样的改正,没有限差的必要。因为二个流派各说各话,互相不能说服对方,以致于JJG703-2008迄今未能出台。
而我其实就是在这时才开始思考一个更深层次的问题:我们凭什么必须把测距仪加乘常数误差归类为系统误差?凭什么测绘界给出的成果的误差就不能归类为系统误差?究竟什么样的测量产生系统误差、什么样的测量产生随机误差?误差分类理论是正确的吗?废弃误差分类概念误差理论能否解释得通?
脑洞大开,随即一篇《误差分类主义批判》成文,列举了众多案例证明误差分类学说实际是自相矛盾、逻辑混乱。后征询名家意见,却被告知这种文体不适合当前学术界,很难发表。果然,几家主流刊物的审稿人都不关心论文给出的案例论据,而都是直接用现有文献为依据来拒稿。后来,该论文只在《2011全国测绘学科博士生论坛论文集》上出版。
总得让主流刊物来为新思想背书才行。终于,2015年,第一篇提出新概念误差理论思想的论文《误差理论的新哲学观》由我国《计量学报》正式发表。
紧接着,2016年,论文《The New Concepts of Measurement Error Theory》由国际测量学联合会(IMEKO)的Measurement杂志发表。
2017年,专著《新概念测量误差理论》由湖北科学技术出版社出版。
2018年,论文《The New Concepts of Measurement Error's Regularities and Effect Characteristics》由国际测量学联合会(IMEKO)的Measurement杂志发表。
这几个出版物都是针对误差分类学说,围绕废弃误差分类学说的测量概念而讨论,更多地是在通过误差分类学说的自相矛盾而讨论误差认识论的哲学问题。但也就是在这个时候才意识到,导致误差分类认知其实还有更深层的原因:数学概念理解问题——传统经典测量理论把常量和变量的数学概念理解错了。
于是,2019年,论文《Comparison of Variance Concepts Interpreted by Two Measurement Theories》经The 5th International Conference on Fuzzy Systems and Data Mining (FSDM 2019)推荐由Journal of Nonlinear and Convex Analysis (JNCA)杂志发表。这篇论文主要说明,测量理论中的方差实际是误差的方差,是一个未知误差的所有可能取值的发散性,是一个未知误差的概率区间评价值,而不是测得值的发散性。测得值是数值,属于常数,在数轴上是一个点,根本没有发散性。按误差的所有可能取值的发散性来理解误差的方差,自然就得出任何误差都有其方差、误差不存在系统/随机分类的结论。
2020年,论文《A New Theoretical Interpretation of Measurement Error and Its Uncertainty》经The 6th International Conference on Fuzzy Systems and Data Mining (FSDM 2019)推荐由 Discrete Dynamics in Nature and Society发表,这篇论文从数学上把测量理论的解释过程进行了一个概括性的推演;同年,论文《Origin and Evolution of Conceptual Differences Between Two Measurement Theories》也发表于Fuzzy Systems and Data Mining VI论文集,这篇论文对二种不同测量理论的概念逻辑的推理过程做了一个全面的对比。
2021年,《测量误差理论的真值中心论和测得值中心论》发表于中国计量科学研究院的《计量科学与技术》杂志,这篇论文再次以中文全面介绍了二种测量理论的不同概念逻辑体系。
2022年,《Mathematical Concepts of Numerical Value and Variable in the Interpretation of Measurement Theory》发表于Journal of Nonlinear and Convex Analysis (JNCA),论文详细阐述了传统经典测量误差理论混淆了常数值和变量的基本数学概念。
但是,学术圈也无非也是这样。
因为知悉了传统测量理论的错误要害,2020年6月,我直接向武汉大学学术委员会和测绘学院教授委员会递交了修改测量误差理论教科书的《学术建议书》,明明白白地告知当前的测量教科书把常数值和变量概念混淆了,违反了数学概念,应当立即纠正以停止其对学生的继续误导。但是,经过几番交流,教授们就是不同意23.4是常数值的观点,他们始终坚持真值才是常量。直到今天,他们也没有给出是否采纳《学术建议书》的回复。我是真替他们担心,将来学生们在课堂上用数学悖论式σ23.4=0.2回怼他们的时候,质问他们“=”号的数学含义的时候,他们将会面临怎样的尴尬呢?
现在看起来,是我太自作多情了,简直就是皇帝不急太监急。这种概念“逻辑”又不是他们发明的,是老师的老师传下来的东西,全世界都一样。既然σ23.4=0.2都是糊弄过去完事,那就继续糊弄呗,犯得着为这种东西伤神吗?既有学术体系的掌握者凭什么要支持自己的反对者呢?自己高高在上不香吗?你搞点新东西就想挤进人家的俱乐部,人家凭什么要解答你出的难题?
一切真理开始时总是在少数人手里,总是受到大多数人的压力。这是一个规律。——科学网好友天津大学杨正瓴博士如是说。
而著名的普朗克原理更如是说,“科学的重大革新很少通过说服反对者并使他们改变立场来实现。事实上倒是,反对者逐渐死去,新生的一代一开始就熟悉新思想。” 西方尚且如此,何况当下这个功利主义的人文环境?当所有的既得利益者选择沉默甚至暗中对抗的时候,你的所有课题申报都不会获批,你将得不到研究经费,连你申报的学生毕业设计课题也能被封杀,你的研究将穷困潦倒,你将无计可施,即使法官也没有办法。
故事就是这样。一个野生的学问,从来不被主流学界看好,不仅未获得过官方支持,反而还受到官方的挤压,自然,它也就不需要再去为主流学界留什么情面了。
当然也曾想过把书稿交由出版社正式出版,像所有的读书人一样,顺便也以此谋求个技术职位的升迁。但是,一者没有募集到出版资金,二者也看透了学术圈里的套路,自然也打消了捞职称的念头,三者则是考虑更有利于学术思想的传播和节约读者的获取成本,于是最终选择了利用互联网免费分享。
和先前出版的个人专著《新概念测量误差理论》相比,本书稿在数学概念上有了更深的挖掘,在不确定度评价原理、离群误差的处理方法、权值分配方法等方面均有了更宽的拓展。欢迎国内外广大读者自由地阅读、研究和传播。
叶晓明
2022 7 于武汉大学
https://blog.sciencenet.cn/blog-630565-1350302.html
上一篇:一目了然的错误测量学概念
下一篇:《测量误差理论解释中的关键数学概念---数值和变量》正式出版