博文
广义线性混合模型之泊松回归模型的R2计算
|
上次跟大家聊了下线性混合模型(lmm)的R2计算方法,这次我们进入稍复杂点的情况,广义线性混合模型(glmm)的R2计算方法。今天我们给大家介绍下,当你的数据为计数数据(count data即数据都为非负整数)的时候,GLMM模型R2的计算方法。对于计数数据, 有几种分布模型可供选择:泊松,伪泊松,负二项,零膨胀等等。我们今天先来介绍GLMM—泊松回归中R2的计算。
首先你要清楚,泊松回归适用的条件是Y是计数数据,且不存在过度离散(理论上,泊松分布的方差=均值,如果实际上方差>均值,那就是出现了过度离散)。我们看下面GLMM案例。
m3 <- glmer(Extinction ~ YearC + TemperatureS + PrecipitationS +
SpeciesDiversityC + (1|Population),
data=biomass, family="poisson")
这个模型的R2应该如何求呢?可能有人觉得,我们直接求这个模型的残差的方差,然后按线性混合模型(LMM)的算法来求R2不可以么。错!当然不可以!因为在GLMM模型中,我们的模型拟合对象,不是y的原始值,而是y的期望值 (也就是模型最终拟合线上的值)。 并且在拟合过程中,我们对 进行了转化(重点:不是对y本身进行了转化)这种转化就是link转换)。对于泊松回归来说,我们进行的一般是log link转换。
即:log( )=b0+b1*x+G,
其中G为随机效应,且G~normal(0, τ)
那么问题来了:这个模型的残差的方差如何算?有人可能会说了,我们直接用y- 不就得到了模型的残差么?对,没错,但问题是这样算的残差是原始尺度的残差,而模型得到的拟合参数(如随机效应的方差)都是是log link尺度下的参数。所以,原始尺度的残差无法转化为log-link尺度下的残差。这导致GLMM的残差的方差难以直接求出。目前统计学家已经提出了一系列理论方法来估算GLMM模型残差的方差,其中最为常用的还是日本大师Nakagawa提出的一系列方法(Nakagawa and Schielzeth 2013, Nakagawa et al. 2017)。我们按出场顺序,向大家一一坐下介绍。
方案1:Nakagawa于2013年提出的最早方案(Nakagawa and Schielzeth 2013)。理论上,对于泊松分布,均值=方差。即y的期望值 的均值=方差。根据这个基本原理,我们可以重新构造一个null model.
m3_null <- glmer(Extinction ~1 + (1|Population),
data=biomass, family="poisson")
这个模型的截距 ,就是log-link尺度下的均值。得到了 之后,依据log(1+ ), 就得到了残差的方差,然后根据模型m3,求
固定效应的方差/(固定效应的方差+随机效应的方差+残差的方差),就得到了R2:

这与performance包下的r2_nakagawa命令的结果一致。

这就是Nakagawa 大师对GLMM 泊松回归模型R2的最初算法。但经历了一番进一步修炼之后,Nakagawa 大师发现这种算法有可能会高估残差的方差,从而低估R2(Nakagawa et al. 2017)。这可能会造成狂热的R2主义者们(大多数科研人员都是)的不满,进而可能影响这种方法的推广。所以大师于2017年又提出了改进后的算法(Nakagawa et al. 2017)。改进后的方法认为,仅依据null model 的截距来计算 还不够,要把随机效应的方差也加上,但要给这个方差除以2,也就是:
![]()
算出来 的均值lambda之后,残差方差的计算又一招变三招,变成了三种计算方法;
方案2:delta法,
方案3:log-normal近似法
方案4:trigamma 法。
这三种方法的其计算方法如下:

这里定义的新变量,就是残差的方差。 那么对应的R2计算当然也就有了三种方法,其计算方法如下:

上述结果与MuMIn包下的r.squaredGLMM命令的结果完全一致:

但就本案例来讲,处lognormal法以外,其他两种方法的R2并没有比原始算法有所升高。
方案5:你也可以用partR2中的partR2命令,来求模型m3的R2, 则会得到:
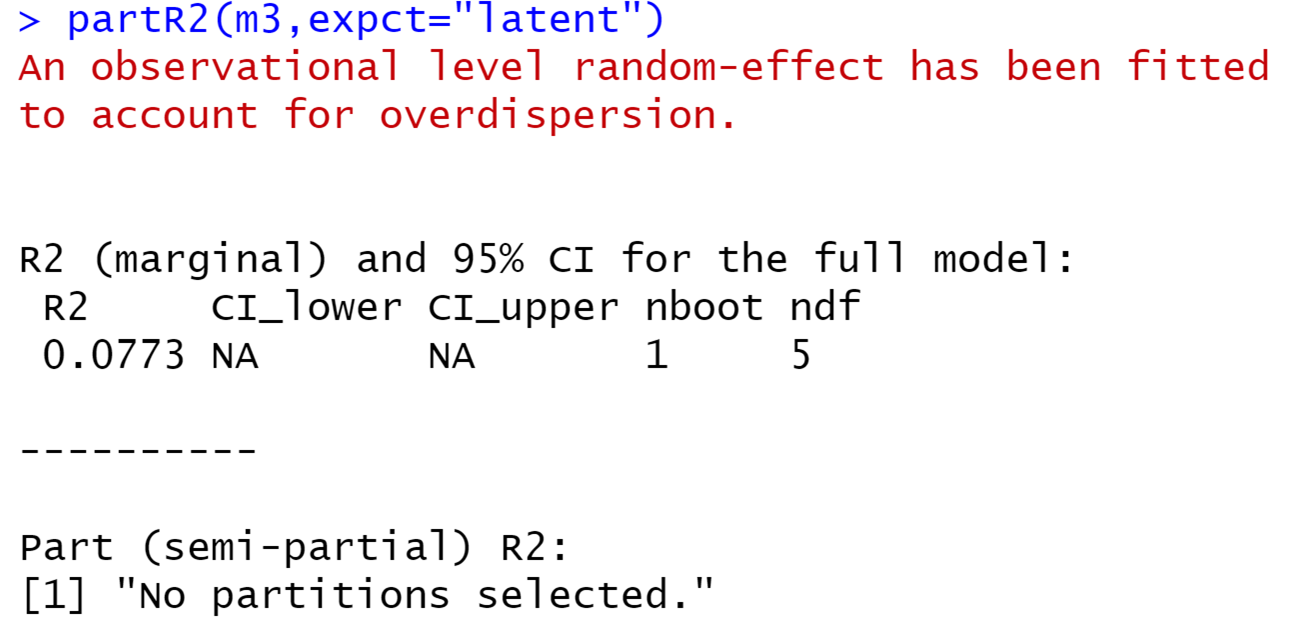
这里设置expct="latent",就是采用日本大师的算法。
注意看,这个结果和上面的四种算法都不相同,是不是哪里出问题呢?别紧张,红字部分其实已经提醒你了:对于计数数据,partR2在求模型R2的时候,强制性的额外添加了一个观测水平的随机效应,以应对Y可能存在的过度离散。这也是目前glmm泊松回归处理过度离散的常用方法。也就是在你的数据里增加新的一列,其值为1,2,3,…n, 其中n就是你的数据的行数(即数据的样本量)。 然后,将这一列变量设置为随机效应。即我们重新拟合1个模型:
m4 <- glmer(Extinction ~ YearC + TemperatureS + PrecipitationS +
SpeciesDiversityC + (1|Population)+(1|obs),
data=biomass, family="poisson")
其中,obs即是观测水平的随机效应。
需要特别说明的是partR2内置的算法中,并没有构造null model,其模型marginal R2的计算,全部依赖full model来完成:

这就与partR2给出的结果完全一致了!但必须明确指出的是,这种算法,跟Nakagawa 2017年定义的算法并不完全一样(没有构造null model),但也不能说一定就是错的,因为这也是计算 的均值的一种方法。
方案6:我们上面设置了expct="latent",以按照Nakagawa算法计算。 其实对于glmm 泊松回归,partR2中还有另一种设置,expct="meanobs", 这种算法简单粗暴,直接以y的原始值的均值,作为其期望值 的均值,其算法如下:

手动计算的结果和partR2的结果完全一致!
综上所述,对于glmm 泊松回归的R2计算,目前有很多种方法。R中不同的包,采用的计算方法有时也并不相同。所以这就要求我们要理解他的背后计算原理,才能做到处变不惊。那么看到这么多计算方法,可能大家就迷惑了,到底采用哪种算法更好呢?按照Nakagawa大师的建议(Nakagawa et al. 2017),首推delta法,也就是r.squaredGLMM函数给出来的第一种R2。
但正如鲁迅他老人家所说:“尽信R, 则不如无R!” r.squaredGLMM这个函数,对于glmm 泊松回归模型的R2计算,没有任何问题。但是,r.squaredGLMM对于glmm的伪泊松模型、负二项模型的R2 计算,竟然都是错的。关于这些错误,鄙人前些天已经发邮件告知了MuMIn包的作者Kamil Bartoń,Kamil Bartoń大师今天也已邮件回复鄙人,目前他已在R-forge上修正r.squaredGLMM函数的错误,并且将尽快在CRAN上更新。关于glmm伪泊松和负二项模型的R2计算方法,以及r.squaredGLMM错在何处,我们下回详细分解!
参考文献:
Nakagawa, S., P. C. D. Johnson, and H. Schielzeth. 2017. The coefficient of determination R(2) and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. Journal of the Royal Society Interface 14:20170213.
Nakagawa, S., and H. Schielzeth. 2013. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods in Ecology and Evolution 4:133-142.
https://blog.sciencenet.cn/blog-3442043-1327038.html
上一篇:混合模型的R2到底是如何计算的?
下一篇:广义线性混合模型(GLMM)伪泊松回归的R2计算