第十七章 再谈线性时不变系统

17.1 宇宙的叛逆者

我们知道，杂乱无章才是宇宙的本质！宇宙的自然趋势是朝着热力学熵与信息熵均最大化的状态演进，即物理上的均匀死寂与认知上的完全随机的混沌，宇宙在整体上遵循一条由有序走向无序（熵增）的宿命之路。但在这条路上却发生了意外，意外地演化出一种名为“智慧体”的反叛力量。这种力量通过利用信息和能量，在局部缔造秩序、对抗无序。激流中逆流而上的智慧体不是 passively 的简单条件反射，而是 actively 强迫症般的创造秩序。内在欲望支配的智慧体组织，总是从宇宙纷繁复杂、看似随机的现象（高信息熵数据）中，提炼出规律、公式和叙事（低信息熵的知识），从而反作用于自然宇宙原本的信息熵增，转变为熵减。

一、“智慧体”的根基--LTI

2001年前后，荷兰和法国的几个研究小组几乎同时实现了数百万个亚稳态氦原子（He*-4）气体中的玻色-爱因斯坦凝聚。实验将数百万个氦原子的所有原子凝聚于单一的、相同的量子基态，具有完全相同的无法区分的波函数，仿若数万亿舞者突然跳起完全同步、整齐划一舞蹈的奇迹。同态、同频、同相的亚稳态氦原子宛若玻色-爱因斯坦凝聚态，宏观上表现为一个整体的量子态，拥有超流、相干等任何单个原子都不具备的全新宏观量子特性。正如同《华严经》“一即一切，一切即一”，“那一个共同的量子态（一）就是整个凝聚体宏观特性（一切）的直接来源和唯一原因；那数万亿个各自不同的原子（一切），在临界条件下丧失个体性，共同构成了那一个纯粹的宏观量子态（一）。“一花一世界，一叶一如来”，是华严宗法界缘起思想的标志性命题，主张个体与整体、部分与全体、具体与普遍之间圆融无碍、相即相入，催生了华严宗从微观到宏观的大一统宇宙观。

进一步看，玻色-爱因斯坦凝聚态（BEC）与线性时不变（LTI）系统息息相关。弱扰动场景下玻色-爱因斯坦凝聚态（BEC）的宏观动力学可近似为线性时不变（LTI）系统，LTI系统的核心数学框架是分析BEC集体激发与线性响应的关键工具。 无/弱相互作用BEC的薛定谔方程是线性时不变动力学方程，原子量子态演化等价于LTI系统的信号传递过程。 BEC线性响应理论（研究弱扰动下的集体模式）完全嵌套LTI系统逻辑，因果性、响应叠加性均与LTI系统准则一致。 强关联BEC的非线性效应是对LTI近似的偏离，LTI框架是分析BEC基态小幅度激发的基础基准。BEC宏观波函数的线性化Gross-Pitaevskii方程满足LTI系统的线性叠加性与时不变性，弱外场（输入）对BEC的激发响应（输出），可通过LTI系统的时域/频域分析（冲激响应、传递函数、傅里叶变换）精准刻画。

LTI系统（线性时不变系统）理论之所以是“智慧体”的基石，是因为它为我们提供了一个完备的、自洽的、且数学上极其优美的工具箱。它允许我们将缤纷繁杂（熵增）的物理世界转化为简单正弦波（熵减），并让我们能够精确地预测和分析系统在这些成分作用下的秩序。

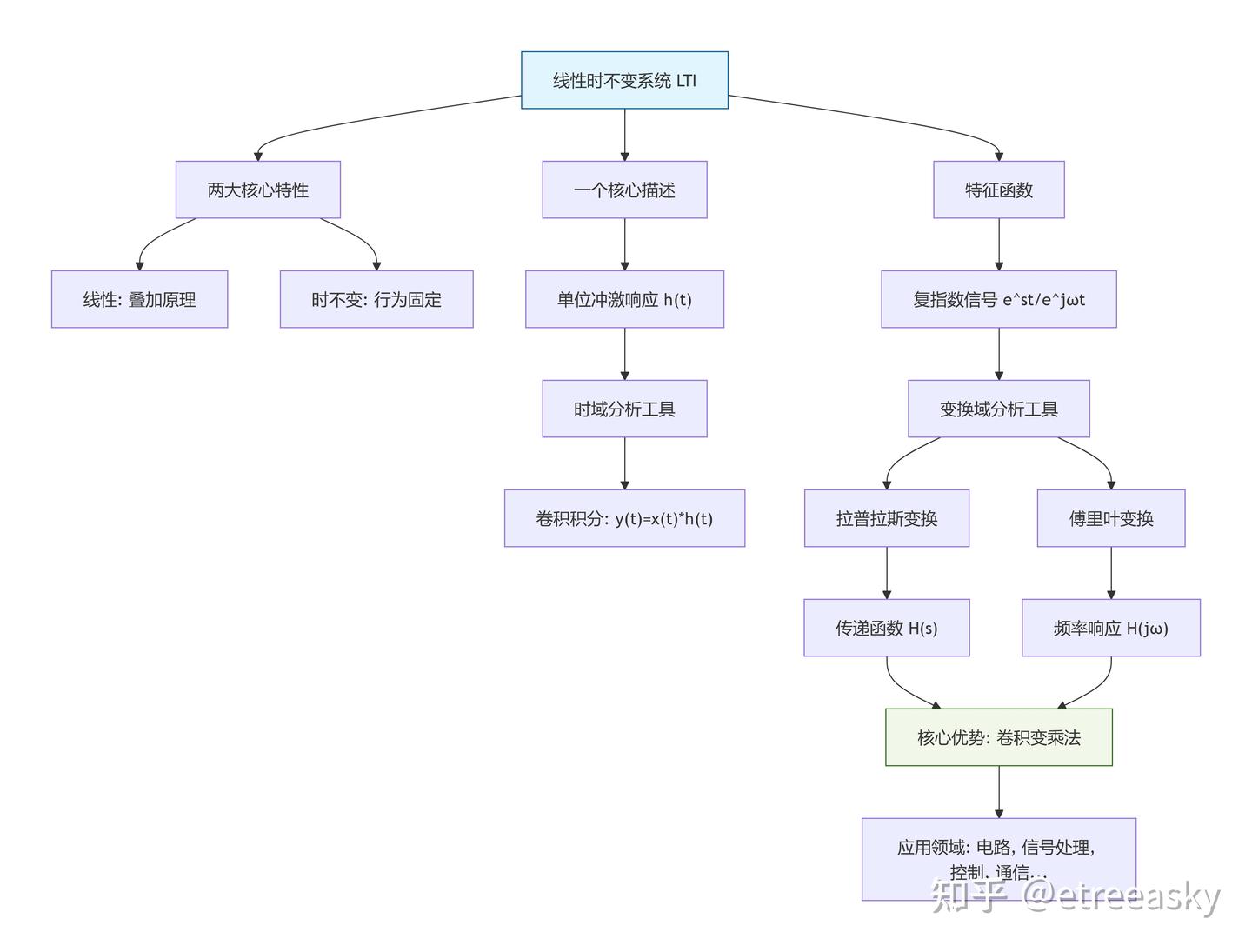
LTI系统无比强大的能力，建立在三个相互关联的数学基石上：

①输入一个理想的瞬间脉冲 δ(t)（狄拉克δ函数），系统产生的输出 单位冲激响应h(t)，对于任何LTI系统，只要知道了它的h(t)，就可以计算出它对任何输入 x(t) 的响应。

②计算工具是卷积积分，系统的输出等于输入信号与单位冲激响应的卷积：

y(t)=x(t)∗h(t)=∫−∞^∞{x(τ)h(t−τ)}dτ

将输入信号 x(t) 看作一连串在时间上排列的加权冲激。每个冲激都会产生一个按 h(t) 形状缩放和延迟的响应。最终的输出 y(t) 就是所有这些被延迟和缩放的冲激响应的叠加（积分）。

卷积是LTI系统的“DNA运算”，根据LTI系统的卷积定理，将时域缤纷繁杂（熵增）信号 x(t) 分解成不同频率 ω 的正弦波的叠加（傅里叶变换），在频域中复杂的卷积运算变成了简单（熵减）的乘法运算：Y(jω)=H(jω)⋅X(jω)

③LTI系统的 “特征函数” 是复指数函数，其复指数信号保持不变性。LTI系统有一个魔法般的性质，如果输入是一个复指数信号 e ^st （其中 s=σ+jω 是一个复数），那么输出将是同一个复指数信号，只是幅度和相位被改变了：est →[ LTI系统 ]→H(s)⋅est，这个复比例因子 H(s) 是系统的传递函数。

当 s=jω（纯虚数）时，输入是正弦/余弦信号 e ^jωt，此时 H(jω) 称为系统的频率响应。它告诉我们系统如何改变不同频率正弦波的幅度（增益）和相位。

二、“智慧体”的身体--同步

单神经元生物没有智能，两个、三个、百、个千个的神经元的生物也没有智能。

但是，一亿个、十亿个、百亿个神经元链接，却诞生了人脑智能，诞生了拥有通用常识智能的chatGPT，这就是神经网络的真正神奇之处。

为什么呢？它们是怎么从量变到质变的呢？

究其根本，这与线性时不变系统的性质密切相关。

先来看看蚂蚁群体一致性行为。在群居生物物种中，切叶蚁表现出了高度复杂行为的物种特征。“切叶蚁形成地球上仅次于人类的最为庞大且复杂的动物社会。”实际上，整天搬叶子的切叶蚁并不吃叶子，它们是用叶子来喂养一种真菌，然后把真菌来作为食物来源。换句话说，它们已经进入了农耕畜牧文明的精准分工协作阶段。切叶蚁群的每一个体，都只是平凡低等的蚂蚁，只懂最简单低级的行为。它们之间交流也仅仅遵循一些简单社会互动和化学气味简单交换规则。虽然切叶蚁群有一个蚁后，但蚁后只负责繁衍后代，蚁后在蚁群中并不发号施令。也就是说，切叶蚁群不存在中央集权体制或领导人。通过切叶蚁我们可以看到，哪怕在去中心化管理组织的社会网络中，也可能通过群落中数百万成员简单互动，而展现的高度智能且复杂的行为。尽管整体蚂蚁群并没有司令官统一指挥调度，蚂蚁群却一点也不象是一群乌合之众，它们精准分工协作的表现比专业教管训练的军队都好。 很奇怪，它们是如何做到的呢？

要保证一个群体不是乌合之众，唯一的办法是规范个体行为与整体行为的某种同步性（一即一切，一切即一）。

如果把个体看作微分dx，整体看作积分∫，“个体行为与整体行为同步”（即微分与原函数保持正比关系）的数学模型为（ 注意，定义域的dt实际上相当于常数）：

当然，实际情况下，“个体行为与整体行为同步”步调一致，并不要求个体步伐与整体步伐跨度一模一样，只要能保持相同比例关系就行，也就是说允许个体与整体有各自常数参数（我的一大步是人类的一小步）：

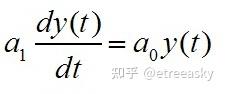
如果我们需要更加细致的考虑同步问题，比如了解蚂蚁四肢每个关节与身体的协调，则可能要研究引入二阶微分来进一步细致量化。步伐一致性数学模型方程添加二阶微分，要素会稍微复杂了点：

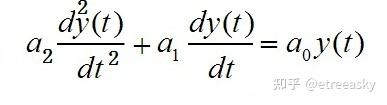
更进一步，如果要细致化到极致的考虑蚂蚁系统更多环节同步问题，则可能要引入更加高阶微分来量化，保持一致性的数学模型难免更加稍微复杂了点：

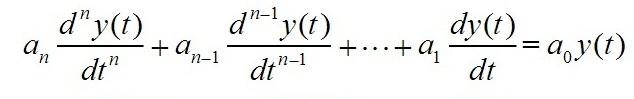
把上式作个小小变形，把原函数y(t)移到等式左边，在把系统反映延迟的常量C代人，得：

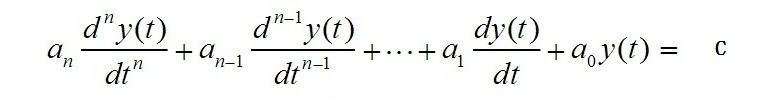
更加复杂一点考虑，如果两个子系统同步，则可以视作是一个稳定系统。比如把y系统和x系统合成一个系统：

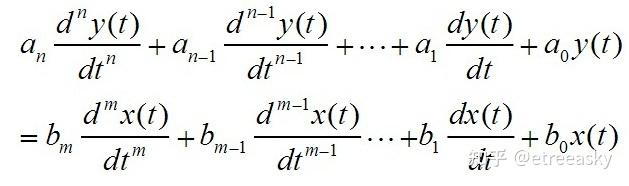
上式中t为自变量(习惯称为时间变量），系数a0、a1......an，b0、b1、......bm均未不随时间变化的常数。看清楚了吗，这样的系统就是线性时不变系统！

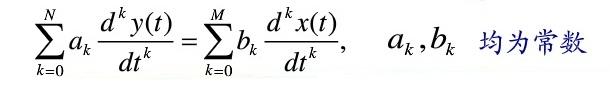
我们知道，既然如果“微分同比例于原函数”（常系数微分方程），则解为指数函数。反过来看，如果某个系统的本征解是复指数函数（比如量子态），这个系统会不会是个常系数微分方程（即线性时不变系统）呢？

且看下面推演（为简化，以无势场薛定谔方程为例）：

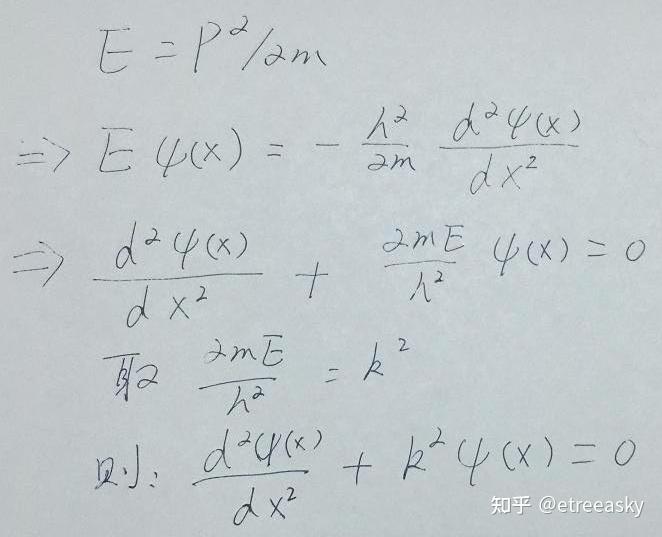
另外，从常系数微分方程数学模型，我们可以看出，要保证群体不崩溃，每一个维度的特征权重值必须是稳定的，也就是说要求每一个体特征不恣意膨胀而保持与整体特征同步。这是一种广义的收敛性，遵从“粒子条件”。请对比常系数微分方程与量子力学的粒子条件：

量子化条件在于哈密顿算子对泊松括号的不变性，指向于系统整体的某种微分不变性，这种数学模型是二维变量下的常系数微分方程。

常系数微分方程组成的系统，最重要的意义在于张量结构，其逻辑模型可以转化为多层线性空间。 线性时不变系统以常系数微分方程为约束条件，是一类特殊张量，可以转换为多层次线性空间。所以，一个单神经元生物是没有智能的，两个三个四个五个神经元也没有智能。一亿个十亿个百亿个神经元链接，却诞生了人脑智能。这是神经网络同步合成的质变。 同步复合的隐含词是：这个系统是线性时不变的。

三、“智慧体”的灵魂--完备性

根据“线性时不变系统”的定义：一个系统是线性且时不变的，当且仅当其系统算符 L 与任意时移算符 D_τ 可交换。即：L{x(t−τ)}=(L{x(t)})∣t→t−τL{x(t−τ)}=(L{x(t)})∣ t→t−τ

①线性算符 (L)：满足叠加原理，L{ax(t) + by(t)} = aL{x(t)} + bL{y(t)}。

②时移/时延算符 (D_τ)：定义为 D_τ{x(t)} = x(t - τ)。

得到，算符交换性：L∘Dτ=Dτ∘L

线性时不变系统中的L∘D τ =D τ​ ∘L ，即线性算符和时延算符的可交换性，即“对易子为零”[L, D_τ] = 0，含义是指所有线性时不变算符的集合，与所有时移算符的集合，各自在复合运算下都构成一个阿贝尔群（满足封闭性、结合律、有单位元、有逆元，且交换律成立）。更重要的是，这两个算符族彼此可交换。这使得对系统的分析（如通过傅里叶变换）变得非常强大。

线性时不变算符 L 的特征函数，是复指数函数 e^{st}（或 e^{jωt}），其中 s 或 ω 是复数频率。关键点是，因为 L 与所有 D_τ 可交换，根据数学理论（如调和分析中的核心定理），L 的特征函数也必须是时移算符 D_τ 的特征函数。而 D_τ 的特征函数也正是这些复指数函数，因为 e^{s(t-τ)} = e^{-sτ} • e^{st}。因此，“它们的共同特征函数——复指数函数——在能量有限信号空间中构成完备正交基。”

在适当的函数空间（如 L² 空间，即能量有限信号空间）中，复指数函数族 {e^{jωt}}（对应不同的频率 ω）构成了一个完备正交基。这就是傅里叶变换的数学基础。任何在该空间中的信号都可以唯一地分解为这些特征函数的线性组合（即频域表示）。

线性时不变系统的核心特性，正是其系统算符与时间平移算符的可交换性。这一对称性直接导致了复指数函数成为系统的特征函数，并最终引出了以傅里叶分析为代表的强大频域分析工具，使得线性时不变系统成为工程和物理学中分析得最为透彻的系统。

线性时不变系统最深刻内含在于，线性算符和时延算符的作用是Abel群，其对应的线性时不变算符（L）与时移/时延算符（D_τ）可交换的，满足乘法交换律，也就是说不存在“对易子”，满足对易关系，它们的共同特征函数（复指数函数）构成完备正交基，其特征基系构成完备系统。

鉴于交换群只是群的特例，线性空间只有流形的一层切空间，满足线性时不变系统条件相对苛刻，所以它的覆盖范围局限。但是LTI系统如同种子，植根于更广范生态中发芽。