博文
为何今年诺贝尔物理学奖颁给两位人工智能学者?谈人工智能的历史变迁及对人类社会的影响  精选
精选
|
2024年10月8日,国庆节放假完第一天,2024年的诺贝尔物理学奖颁给了两位人工智能学者,约翰·霍普菲尔德(John Hopfield)和杰弗里·辛顿(Geoffrey Hinton),因为他们通过人工神经网络对机器学习方面形成的奠基性贡献。我相信这结果让大多数物理学家大失所望,毕竟物理学方面的成就也不少。自1901年首次颁奖开始,历届的物理学奖也从未给过其它专业的科学家,倒是反过来的有,比如居里夫人,1911年因发现元素钋(Polonium,对她出生国波兰的纪念)和镭获得诺贝尔化学奖,成为第一个两获诺贝尔奖的人。

图1: 约翰·霍普菲尔德(左)和杰弗里·辛顿(右)(图来自网络)
不过,约翰·霍普菲尔德和杰弗里·辛顿获得诺贝尔物理学奖,估计让人工智能学者也同样大吃一惊。毕竟人工智能界的最高奖通常是图灵奖,是为纪念人工智能图灵所设。辛顿在2018年和他两学生Yoshua Bengio, Yann LeCun(杨立昆,中译名)因对深度学习的贡献获得图灵奖,估计已经知足了,没想到还有大奖在后面。而另一让人工智能学者吃惊的可能是,为啥霍普菲尔德能拿诺奖。从1936年图灵提出想模拟人类智能的图灵机开始,杰出的人工智能学者层出不穷,为啥霍普菲尔德能够胜出呢?下面以我个人的理解,来简单聊聊两位人工智能科学家的贡献。

图2: 2018年图灵奖获得者
辛顿是大家熟悉的,他的成名作是与Rumelhart以及Williams于1986年在《Nature》上发表的误差反向传播算法。该算法让神经网络经历第一波寒冬后,重新走向人工智能的舞台。尽管该算法在数学界很早就有相关的研究,但应用于神经网络则是从1986年开始。只是,反向传播算法引发的热潮,在1995年左右很快又被统计机器学习盖过去,因为后者在当时既有严格的理论保证,也有比当时的神经网络更为出色的性能。结果,有将近20年的时间,人工智能的主流研究者都在统计机器学习方面深耕。即使2006年辛顿在《Science》上首次提出深度学习的概念,学者们仍然将信将疑,跟进的不多。
直到2012年,辛顿带着他的学生Alex在李飞飞构建的ImageNet图像大数据上,用提出的Alex网络将识别性能比前一届一次性提高将近10个百分点,这才让大部分的人工智能学者真正转向深度学习,因为以之前每届用统计机器学习方法较上一届提升性能的速度估计,这次的提高需要用20多年时间。
自此以后,人工智能开始相信,大数据、算力、深度模型,是走向通用人工智能的关键三要素。科学家们想到了各种各样的方式来增广数据,从对图像本身的旋转、平移、变形来生成数据、利用生成对抗网来生成、利用扩散模型来生成;从人工标注到半人工到全自动机器标注。而对算力的渴望也促进了GPU显卡性能的快速提升,因为它是极为方便并行计算的。但它也导致了对我国人工智能研究的卡脖子,因为目前几乎绝大多数学者和人工智能相关企业都认为硬件是对大数据学习的核心保障。深度模型的发展也从最早的卷积神经网络,经历了若干次的迭代,如递归神经网络、长短时记忆网络、生成对抗网、转换器(Transformer)、扩散模型,到基于Transformer发展而来的预训练生成式转换器(GPT),以及各种GPT的变体。
回过头来看,这些研究与辛顿在人工智能领域、尤其是人工神经网络方面的坚持是密不可分的。
当然,辛顿的坚持并不意味着他只认定一个方向。实际上,他对人工智能真谛的探索一直是有转变的。记得某年神经信息处理顶会(NIPS,Neural Information Processing Systems)会议曾做过一个搞笑视频,讲述辛顿对大脑如何工作的理解,从1983年的玻尔兹曼机、到86年的反向传播、到对比散度、再到06年的深度学习,经历过多次的变迁。如果用机器学习的表述来理解辛顿的观点,可以说依某个小于1(1表示确定,0表示否定)的概率成立。
再说说霍普菲尔德。他的主要贡献是1982年提出的Hopfield网络,如果从发表的时间节点来看,当时没有反向传播算法,这个网络的初期版本自然是无法通过误差反向来调优的。
但这个网络当时发表在PNAS期刊上,文章的标题里有一个与物理相关的单词“Physical Systems”。网络的主要想法是,如果按物理学讲的能量函数最小化来构造网络,这个网络一定会有若干最终会随能量波动稳定到最小能量函数的状态点,而这些点能帮助网络形成记忆。同时,通过学习神经元之间的联接权值和让网络进行工作状态,该网络又具备一定的学习记忆和联想回忆能力。
另一个与物理相关的是,构造该网络的设计思路模拟了电路结构,假定网络每个单元均由运算放大器和电容电阻组成,而每一个单元就是一个神经元。
不过,这个网络从当时看,还是存在诸多不足的。比如只能找到局部最小值。但更严重的问题是:
尽管从神经生理学角度来看,这个网络的记忆能对应于原型说,每个神经元可以看成是一个具有某个固定记忆的离散吸引子(Discrete Attractor),但它的记忆是有限的,且不具备良好的几何或拓扑结构。
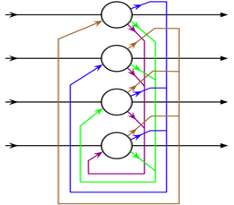
图3:Hopfield网络结构图,1982。圆形节点代表可形成记忆的神经元,相互联接的线反映了神经元之间联系的权重。
图4: Kohonen网络,1989
所以,便有了很多在此基础上的新方法的提出。比如1989年的Kohonen网络在设计时就假设有一张网来与数据云进行匹配,通过算法的迭代最终可以将网络完好地拟合到数据上,而网上的每个节点便可以认为是一个记忆元,或离散吸引子。这样的网络有更好的拓扑或几何表征。
另外,关于人的记忆是不是应该是离散吸引子,至今也没有终结的答案,比如2000年左右就有一系列的流形学习文章发表(Manifold learning)。这些文章在神经生理学方面的一个重要假设是,人的记忆可能是以连续吸引子形式存在的。比如一个人不同角度的脸,在大脑记忆时,吸引子可能是一条曲线的形式,或者曲面、或者更高维度的超曲面。人在还原不同角度的人脸时,可以在曲面上自由滑动来生成,从而实现更有效的记忆。在此理念下,仅考虑离散吸引子的Hopfield网络及其变体,自然就少了很多跟进的研究者。
当然,流形学习的研究实际上后期也停顿了,因为这方面的变现能力不强。
随着深度学习的兴起,大家发现通过提高数据量、加强算力建设、扩大深度模型的规模,足以保证深度学习能实现好的预测性能,而预测性能才是保证人工智能落地的关键要素。至于是否一定要与大脑建立某种关联性,是否一定要有好的可解释性,在当前阶段并不是人工智能考虑的重心。
也许,等现有的大模型出现类似计算机一样的摩尔定律时,人工智能会回归到寻找和建立与大脑更为一致、更加节能、更加智能的理论和模型上。
再回到人工智能与诺奖的关系。从今年诺贝尔物理学奖的得奖情况,和人工智能近年来对几乎全学科、所有领域的融入程度来看,也许,未来学好人工智能,很有可能会比拒绝人工智能的人,能更有效的工作、生活、形成新的重要发现,甚至争夺各个方向的诺贝尔奖。
张军平写于2024年10月8日晚
https://blog.sciencenet.cn/blog-3389532-1454347.html
上一篇:失控:脑补的生成式AI
下一篇:为什么诺贝尔化学奖又被人工智能学者拿了:阿尔法折叠,蛋白质结构预测易手