博文
如何证明勾股定理?
||
英国科学刊物《Physics World》曾经让读者评选“历史上最伟大公式”,最终入选的十大公式中包括著名的几何定理——勾股定理:直角三角形两直角边的平方和等于斜边的平方。
勾股定理,也称毕达哥拉斯定理。毕达哥拉斯是希腊哲学家、数学家,生于约公元前570年,卒于公元前500-490年。西方学者认为,毕达哥拉斯第一个证明了该定理。但是,一位现代数学家偶然发现了一块古巴比伦石碑,表明该定理可能在毕达哥拉斯诞生前1000多年就已存在。这块石碑提出了一个类似于毕达哥拉斯定理定理的概念。数学的核心支柱之一是证明的概念。现在流传下来毕达哥拉斯定理的第一个严格证明是在公元前300年前后,欧几里得在其编撰的《几何原本》(成书于公元前300年左右的)里给出的。
在我国古籍《周髀算经》(约成书于公元前1世纪)中,对勾股定理有过明确的记载:“若求邪至日者,以日下为勾,日高为股,勾股各自乘,并而开方除之,得邪至日。”。《周髀算经》中还记载:“勾广三,股修四,径隅五”。这里也没有给出勾股定理的具体证明,“三”、“四”、“五”只是勾股三元数组的特例(在公元前1800年巴比伦人的文字泥板中,也发现过有15行勾股三元数组)。后来,三国时期东吴数学家赵爽在其所著的《周髀算经注》,利用“赵爽弦图”给出了勾股定理的精巧证明。相比欧几里得在《几何原本》中介绍的方法,赵爽的证明方法更简洁、优美。“赵爽弦图”现在被称为“中国古代数学的图腾”,并曾作为在2002年北京召开的世界数学大会的会徽,2021年在上海召开的第十四届国际数学教育大会的会徽中心也镶嵌了赵爽弦图。
勾股定理现有500种以上证明方法,是数学定理中证明方法最多的定理之一。本博文介绍其中的7种,包括欧几里得、赵爽、著名物理学家阿尔伯特·爱因斯坦和曾任美国总统的詹姆斯·加菲尔德等是如何证明勾股定理。
(一)欧几里得《几何原本》如何证明毕达哥拉斯定理?
对于直角三角形△ABC,假设其斜边AB长c,两个直角边CA和BC分别长a和b。欧几里得在《几何原本》中的证明使用了下面的图形:
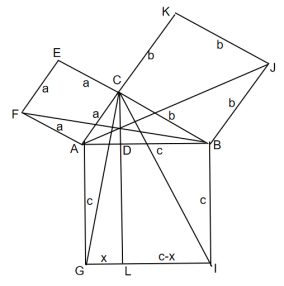
首先,以CA、AB、BC为边做正方形□CEFA、□AGIB、□CBJK。我们需要证明□AGIB面积=□CEFA面积+□CBJK面积。
过点C作CL平行于AG,将正方形□AGIB分成两部分:矩形AGLD和矩形DLIB。
连接CG、BF,构成△CAG和△FAB。△FAB和△CAG全等(除了旋转了一个角度)。
因为△CAG与矩形AGLD共底AG,且在平行线AG、CL之间,所以,矩形AGLD面积=2△CAG面积。
因为△FAB与正方形□FACE共底AC,且在平行线FA、EB之间,所以,□FACE面积=2△FAB面积。
因为△FAB面积=△CAG面积,所以,□FACE面积=矩形AGLD面积。记GL长度为x,即
连接AJ、CI,构成△CIB和△ABJ。同理,矩形DLIB面积等于□CBJK面积。LI长度为c-x,即,

所以,得到:
证毕。
(二)赵爽弦图如何证明勾股定理的?
赵爽在为《周髀算经》作注解时,其中,530余字的“勾股圆方图”注文,给出了勾股定理证明方法。
设直角三角形的两个直角边长分别为a和b,斜边长c,赵爽将四个直角三角形的直角边拼在一起,形成了一个大正方形,称之为弦图。
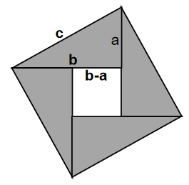
这个大正方形的边长为弦长c,所以大正方形的面积为
大正方形又是由一个小正方形(边长b-a),四个直角三角形(两个直角边的长度分别是a和b)构成的,所以面积S应该等于:
因此,得到
证毕。
(三)利用相似三角形的性质证明勾股定理
从直角三角形△ABC的直角顶点C向斜边AB画一条垂线CD,将原来的直角三角形分成两个小三角形△DBC和△DCA。假设,BC长a,CA长b,AB长c,DB长c1,DA长C2。
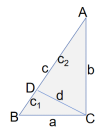
由于△ABC和△DBC相似,即
 -------(1)
-------(1)
由于△ABC和△DCA相似:
-------(2)
将(1)和(2)相加,得到
因为(c1+c2)= c,得到:
证毕。
(四)爱因斯坦提出的证明方法
假设直角三角形两个直角边长是a和b,斜边长c。阿尔伯特·爱因斯坦在11岁时(1890年)提出的证明方法,也是从直角顶点向三角形斜边画一条垂线,把三角形分成两部分:把斜边为a的直角三角形记为①,斜边为b的直角三角形记为②。把①、②和原来的直角三角形一起排成一排,并以各自的斜边为边,画一个正方形,其面积分别为a2,b2和c2。
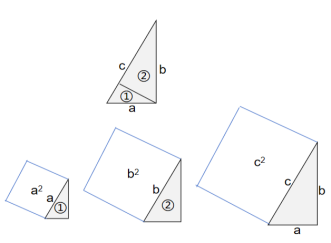
这三个图形完全相似,三角形部分与正方形部分面积比相同,假设为m。也就是说,三个三角形面积分别是ma2,mb2和mc2。由于原来的直角三角形的面积等于三角形①和②面积之和,即
消除比例系数m,得到:
证毕。
(五)加菲尔德证明方法
1876年,英裔美国政治家、数学家詹姆斯·艾伯拉姆·加菲尔德(后来曾当选美国第20任总统),在《新英格兰教育日志》上发表了他对勾股定理的一种证法。
假定直角三角形ABC,斜边AB长c,两个直角边BC和CA分别长a和b。加菲尔德的方法是用两个全等直角三角形,构成如下图的梯形BCEA,。

证毕。
(六)加菲尔德证明方法的变种
加菲尔德证明方法是用两个全等直角三角形摆成梯形,如果用四个全等直角三角形摆成正方形,则可以更简洁地证明。
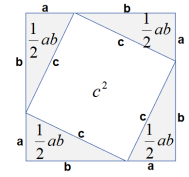
如图所示,由四个全等直角三角形(直角边为a和b)和一个正方形(边长为c)构成了一个大正方形(边长为a+b)。因此,
证毕。
(七)一种一目了然的证明方法
最为一目了然的证明勾股定理方法,是分别用四个全等直角三角形(假设直角三角形的两个直角边长为a和b,斜边长c),摆成两个正方形(注意,左边的图和前面加菲尔德证明方法变种用的图一样):右边图的两个白色正方形面积之和与左边图的白色正方形面积相等。也就是:a的平方加上b的平方,等于c的平方:
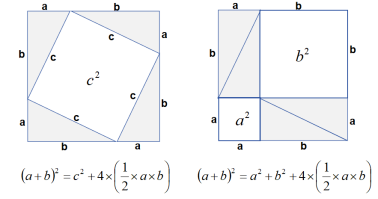
证毕。
https://blog.sciencenet.cn/blog-3005681-1407867.html
上一篇:MilliMobile自动驾驶机器人由光或无线电波供电
下一篇:约翰逊-杰克逊的证明
全部作者的精选博文
- • 人类理解宇宙的基石
- • 古代文明的智慧结晶
- • 一个颠覆传统认知的科学发现
- • 史上最著名的悖论
- • 漫谈伯特兰悖论和伯特兰盒子悖论
- • 漫谈“男孩或女孩”悖论
全部作者的其他最新博文
- • 人类理解宇宙的基石
- • 跨越时空的数学瑰宝
- • 古代文明的智慧结晶
- • 一个颠覆传统认知的科学发现
- • 史上最著名的悖论
- • 漫谈伯特兰悖论和伯特兰盒子悖论