博文
约翰逊-杰克逊的证明
||
在美国数学学会的一次会议上,两位高中生展示了她们利用三角学证明毕达哥拉斯定理(即,勾股定理)的一种新的方法——这类方法曾被一些人认为是不可能的。数学家伊莉莎·卢米斯(Elisha Loomis)在其1927年的著作《毕达哥拉斯定理》中指出,毕达哥拉斯定理的任何三角学证明都是不可能的。卢米斯认为,如果你在证明毕达哥拉斯定理时使用三角函数,会是一个循环论证。三角学的大多数基本规则本身都是基于毕达哥拉斯定理的,这意味着任何这样的证明可能成问题。但是,实际上,三角学中的有些结果独立于毕达哥拉斯定理,例如,正弦定理,正弦和余弦比值。
2023年3月18日,新奥尔良圣玛丽学校的高中生卡尔恰·约翰逊(Calcea Rujean Johnson)和奈基娅·杰克逊(Ne'Kiya Jackson)在美国数学学会东南分会春季会议上发表了一篇演讲摘要,提出了毕达哥拉斯定理的一个新证明,正是基于三角学中的正弦定理。一些数学家对这个新的证明感到兴奋。
约翰逊-杰克逊是如何证明的呢?假设三角形两个直角边长为a和b,斜边长c。她们在图中添加更多的三角形(图1):首先,她们通过在一边添加它的镜像来对折原始三角形;然后她们延伸这个镜像三角形的斜边,直到它与一条垂直于原始斜边的线相连。结果是一个新的直角三角形——两个直角边的边长为c,X,斜边为Z。
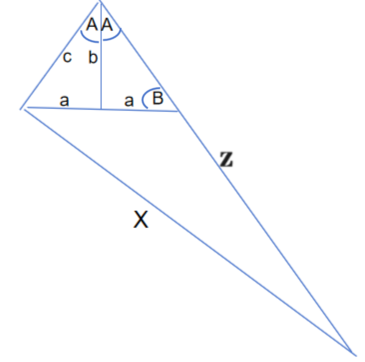
图1
约翰逊和杰克逊用了正弦定理——假设任意一个三角形的边长为a、b、c,如果把与边a相对的角标为角A,与边b相对的角标为角B,与边c相对的角标为角C,则sinA/a=sinB/b=sinC/c。
注意,图1上部原始三角形及其镜像构成一个等腰三角形(边长为c、c、2a),根据正弦定理:
由于
因此,
...........(1)
证明的后一部分是将这个大三角形细分成无限多个小的直角三角形,它们都与原始三角形相似。约翰逊和杰克逊注意到,当继续沿着这个无限下降时,连续的三角形之间的相应边长比率是a/b。注意,斜边沿线X的相邻三角形的斜边比率是a2/b2,斜边沿线Z的相邻三角形斜边比率也是a2/b2,如同图2所示。这里边长的计算只要用正弦定理。
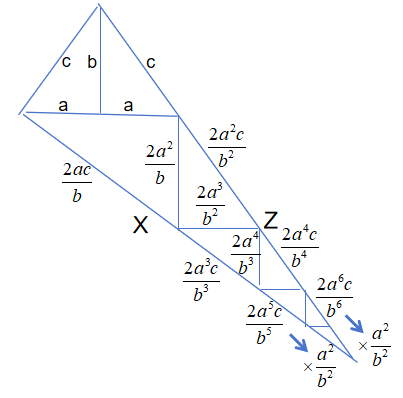
图2
由
得到
由
得到
因此,
..........(2)
比较(1)和(2),得到:
证毕。
结语
勾股定理(即,毕达哥拉斯定理)被称为“数学皇冠上的明珠”。德克萨斯A&M大学商学院数学荣誉退休教授斯图尔特·安达臣说,这个定理“连接了代数和几何”。“语句a2 + b2 = c2,那是一个代数语句。但它的来源是一个几何图形。”
我国周朝时期的商高就提出了“勾三股四弦五”的勾股三元数组的特例。根据加州大学洛杉矶分校计算机科学系的说法,古巴比伦和埃及的学者也知道这个定理,它显示在一个有4000年历史的巴比伦石碑上。所以,它可能至少有4000年的历史。勾股定理至今已经出现500种以上证明方法,大家可能会认为不会有太多新的东西要出现。
今年春天,约翰逊和杰克逊的证明,成为西方许多科技网站报道的焦点,报道大多强调两个高中生发现了勾股定理的“不可能”证明。
两位中学生的探索精神可嘉,美国数学会邀请中学生做报告,也值得称赞。不过,就证明方法本身而言,我还是更喜欢我国三国时期东吴数学家赵爽的证明——直观、简洁(见本博文的附录)。
这里介绍的约翰逊-杰克逊证明过程主要依据参考资料[1]~[3]。我在写这个博客后,发现有一个问题:如果a=b,图1的线Z和线X平行,构不成大三角形。这是否一个漏洞?能够堵塞这个漏洞吗?据报道,美国数学学会(American Mathematical Society)鼓励这两人将他们的结果提交给同行审查,但,几个月过去了,还没有看到有关报道。
参考资料:
[1] Tesfaye Negussie. 2 New Orleans teenagers say they proved the 2,000-year-old Pythagorean Theorem.March 31, 2023.https://abcnews.go.com/US/2-new-orleans-teenagers-proved-2000-year-pythagorean/story?id=98207106
[2] Leila Sloman. 2 High School Students Prove Pythagorean Theorem. Here’s What That Means. April 10, 2023
https://www.scientificamerican.com/article/2-high-school-students-prove-pythagorean-theorem-heres-what-that-means/
[3] Two High School Students Discover "Impossible" Proof Of The Pythagorean Theorem.https://www.iflscience.com/two-high-school-students-discover-impossible-proof-of-the-pythagorean-theorem-68455
附录:
在上一篇博文《如何证明勾股定理》中介绍过历史上7种证明方法。这些证明有的独特而奇妙的,有的简洁而优美。为了与杰克逊和约翰逊的证明方法比较,把这些证明过程的要点图示如下。

图A 欧几里得的证明

图B 赵爽证明

图C 利用相似三角形的性质证明

图D 爱因斯坦提出的证明

图E 加菲尔德证明
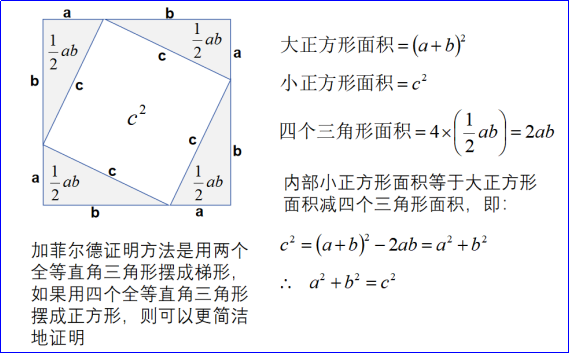
图F 加菲尔德证明方法的变种

图G 一目了然的证明
https://blog.sciencenet.cn/blog-3005681-1408600.html
上一篇:如何证明勾股定理?
下一篇:比内特公式
全部作者的精选博文
- • 人类理解宇宙的基石
- • 古代文明的智慧结晶
- • 一个颠覆传统认知的科学发现
- • 史上最著名的悖论
- • 漫谈伯特兰悖论和伯特兰盒子悖论
- • 漫谈“男孩或女孩”悖论
全部作者的其他最新博文
- • 人类理解宇宙的基石
- • 跨越时空的数学瑰宝
- • 古代文明的智慧结晶
- • 一个颠覆传统认知的科学发现
- • 史上最著名的悖论
- • 漫谈伯特兰悖论和伯特兰盒子悖论