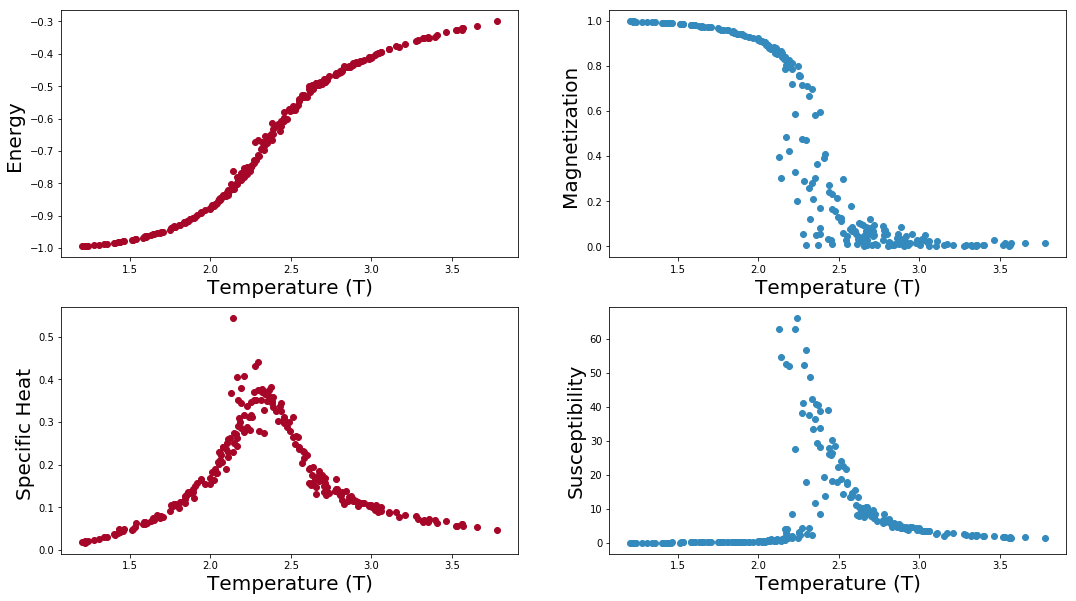
2维伊辛模型 数值模拟
算法
♦ 选择一个格点i, 其自旋将考虑作翻转 si =-si.
♦ 计算与此翻转相联系的能量变化 dH.
♦ 计算这一翻转的转移几率 w.
♦ 产生一在 [0,1] 之间均匀分布的随机数 x.
♦ 如果x<w, 则翻转该自旋, 否则, 保持不变. 不论何种情况, 其结果都作为一新的状态.
♦ 分析该状态, 为计算平均值收集数据.
以下代码在2D中模拟Ising模型。
能量,磁化,比热和磁化率已被计算和绘制。
from __future__ import divisionimport numpy as npfrom numpy.random import randimport matplotlib.pyplot as plt#----------------------------------------------------------------------def initialstate(N):
''' generates a random spin configuration for initial condition'''
state = 2*np.random.randint(2, size=(N,N))-1
return statedef mcmove(config, beta):
'''Monte Carlo move using Metropolis algorithm '''
for i in range(N):
for j in range(N):
a = np.random.randint(0, N)
b = np.random.randint(0, N)
s = config[a, b]
nb = config[(a+1)%N,b] + config[a,(b+1)%N] + config[(a-1)%N,b] + config[a,(b-1)%N]
cost = 2*s*nb
if cost < 0:
s *= -1
elif rand() < np.exp(-cost*beta):
s *= -1
config[a, b] = s
return configdef calcEnergy(config):
'''Energy of a given configuration'''
energy = 0
for i in range(len(config)):
for j in range(len(config)):
S = config[i,j]
nb = config[(i+1)%N, j] + config[i,(j+1)%N] + config[(i-1)%N, j] + config[i,(j-1)%N]
energy += -nb*S
return energy/4.def calcMag(config):
'''Magnetization of a given configuration'''
mag = np.sum(config)
return magnt = 2**8 # 温度点数量N = 2**4 # 点阵尺寸, N x NeqSteps = 2**10 # MC方法平衡步数mcSteps = 2**10 # MC方法计算步数n1, n2 = 1.0/(mcSteps*N*N), 1.0/(mcSteps*mcSteps*N*N)tm = 2.269; T=np.random.normal(tm, .64, nt)T = T[(T>1.2) & (T<3.8)]; nt = np.size(T)Energy = np.zeros(nt); Magnetization = np.zeros(nt)SpecificHeat = np.zeros(nt); Susceptibility = np.zeros(nt)---------------------------------------------------------------------for m in range(len(T)):
E1 = M1 = E2 = M2 = 0
config = initialstate(N)
iT=1.0/T[m]; iT2=iT*iT;
for i in range(eqSteps): # equilibrate
mcmove(config, iT) # Monte Carlo moves
for i in range(mcSteps):
mcmove(config, iT)
Ene = calcEnergy(config) # calculate the energy
Mag = calcMag(config) # calculate the magnetisation
E1 = E1 + Ene
M1 = M1 + Mag
M2 = M2 + Mag*Mag
E2 = E2 + Ene*Ene
Energy[m] = n1*E1
Magnetization[m] = n1*M1
SpecificHeat[m] = (n1*E2 - n2*E1*E1)*iT2
Susceptibility[m] = (n1*M2 - n2*M1*M1)*iTf = plt.figure(figsize=(18, 10)); # plot the calculated values sp = f.add_subplot(2, 2, 1 );plt.plot(T, Energy, 'o', color="#A60628");plt.xlabel("Temperature (T)", fontsize=20);plt.ylabel("Energy ", fontsize=20);sp = f.add_subplot(2, 2, 2 );plt.plot(T, abs(Magnetization), 'o', color="#348ABD");plt.xlabel("Temperature (T)", fontsize=20);plt.ylabel("Magnetization ", fontsize=20);sp = f.add_subplot(2, 2, 3 );plt.plot(T, SpecificHeat, 'o', color="#A60628");plt.xlabel("Temperature (T)", fontsize=20);plt.ylabel("Specific Heat ", fontsize=20);sp = f.add_subplot(2, 2, 4 );plt.plot(T, Susceptibility, 'o', color="#348ABD");plt.xlabel("Temperature (T)", fontsize=20);plt.ylabel("Susceptibility", fontsize=20);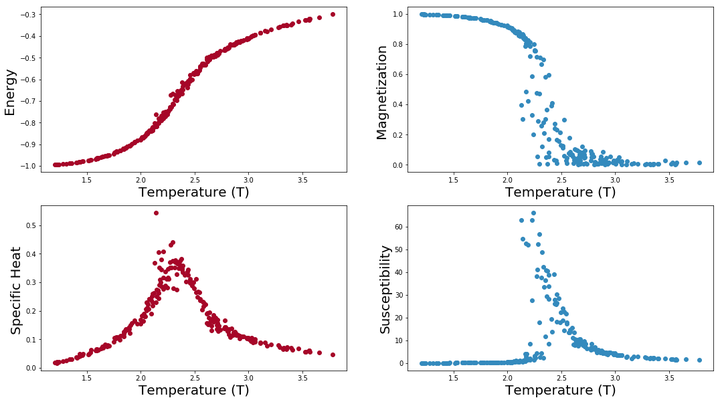

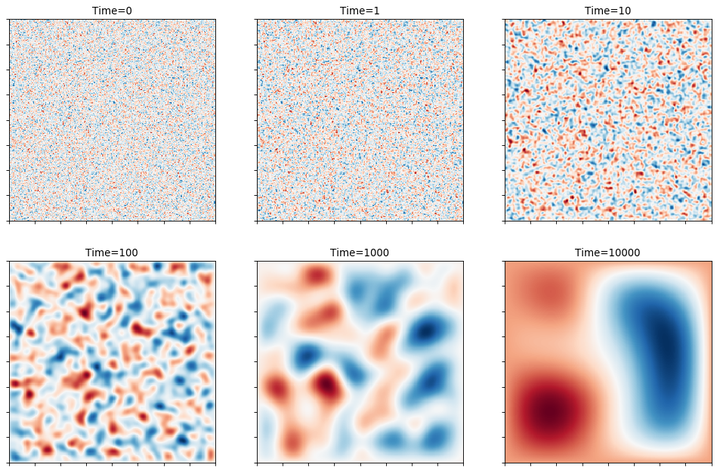
计算能量差是最费时的工作,对于Ising 模型, 由于能量差只能取很少几个数值, 我们可以予先算好存起来以节省计算量. 这一技巧不仅适用于Ising 模型, 也适用于其它分立变量的模型如
Potts 模型等.
例如, 对于正方格子上的Ising模型, 每个自旋(设为s0)有四个近邻, 设为s1, s2, s3, s4, 则s0与近邻的相互作用能量为:
翻转一个自旋可能的能量差为
于是
求出dE0 和exp(-\beta d E0)的几个数值并保存下来,可以节省很多计算时间.