博文
警惕:别让对统计结果的误读误导科学研究(二)
 精选
精选
|
(二)数据分布对R2的影响
除本质性关联外,数据分布同样会影响回归分析的R2,进而影响因子(或回归方程)的显著性。多数研究中认为,只有P值低于0.05(即,95%以上的可能性)才认为该因子具有显著性(实际上,这一原则可能过于教条与苛刻)。因此,数据分布的影响可能对相关因子的评判产生本质性差别(即,显著与不显著的区别)。数据分布对R2的影响可以通过其计算公式推导出来(我都尝试过),不想弄得太复杂,故不在此给出相关推导,仅以下面三种情况举例说明:
(1)数据离群值的影响:实际研究中,多种原因都可能导致离群值的出现。这种离群值不一定是错的,但远离绝大多数数据的分布范围。在大样本分析中,这种离群值还可能不只一两个,它们的存在会对统计分析结果造成巨大影响。一个极端点儿例子:100次观测中有99次观测在1-10之间变化,仅第100次观测为100。如果回归分析包括第100次观测,R2可能会接近于与1。此时接近于两点间的回归分析,前面99个点几乎相当于一个点。在此情况下,即使R2再高,回归方程的残差也不会符合正态分布,注定不是一个成功的回归分析。相反,如果剔除第100次观测,回归方程甚至可能达不到统计学意义上的显著性。因此,一个异常值的剔除与否可能带来两种完全不同的评判。被鉴定为显著的因子会被继续关注,不显著的因子从此被“打入冷宫”。此时,正确的选择是基于一些公认的数学方法进行异常值剔除。但可能会面对一个巨大无比的“帽子”:人为筛选数据。
在此分享两个亲身经历:(1). 2018年发表的一篇大样本分析文章中,我们只采用了数据库中1-99百分位(Percentile)的数据,剔除了其中约2%的数据。审稿过程中,评委质疑我们剔除这些数据的理由,认为:剔除任何数据都需要联系原始文献的通讯作者,让他/她承认数据有问题才行。这显然是一个不可能完成的任务,有几个人会公开承认自己的数据是错的?当时,我们是这样回答的:没有包括这一部分数据并不是因为它们错了,而是因为它们位于样本总体分布的边缘,属于小概率事件。我们不怀疑这些数据在特定条件下的正确性,但它们不适合被包括在我们的大样本分析中。因为,大样本分析应该侧重于数据的总体规律,而不是关注少数情况下才出现的现象。第二次返修时,评委没有再提类似问题,算是过关了。(2). 在一次半开放的学术交流中,我介绍了几种剔除异常值的常见方法(很多统计学教材中都有讲述)。结束后一位教授提出:不管采用何种方法,从已有数据库中剔除数据都有“人为筛选”的嫌疑。当时我愣了住了,一时不知道怎么回答。片刻后,我举了两个例子:一个农民在播种玉米时发现一粒种子已经发霉,还坚持把它播种下去,那是犯傻;一个姑娘在相亲时发现对方是流氓,还坚持嫁给他,那是犯贱。例子的确不好听,但至少明确表达了我的看法。
(2)数据变异范围的影响:在多因子体系中,如果某一自变量的变异范围过窄,它对因变量的影响很可能被其它自变量所掩盖。在表象上表现为对因变量没有显著影响。我们曾经推导过:变量变异范围越窄,回归分析达到显著性水平(即,P < 0.05)的可能性越低(图1a)。以温度对有机碳周转速率的影响为例:局地研究中温度的变异范围一般较窄,所以不少研究发现温度与有机碳周转速率没关系。但是当把这些局地结果放在一起时,温度变异范围超过了30℃。此时的回归分析表明:温度是影响有机碳周转速率的极显著因子(即,P < 0.01)(图1b),而且这些局地数据绝大多数被涵盖在回归方程的预测区间内(图1b中红虚线范围)。又如:一项在某地区开展的调查研究发现,土壤有机碳周转速率与粘粒含量之间没有显著相关性。但是同一批作者在整合全球数据后发现,粘粒含量是影响有机碳周转速率的显著性因子。同一因子的显著性在不同研究中经常不同,很多情况下都是因子变异范围的差别造成的。“管中窥豹”、“瞎子摸象”等典故能很好地表达类似意思。
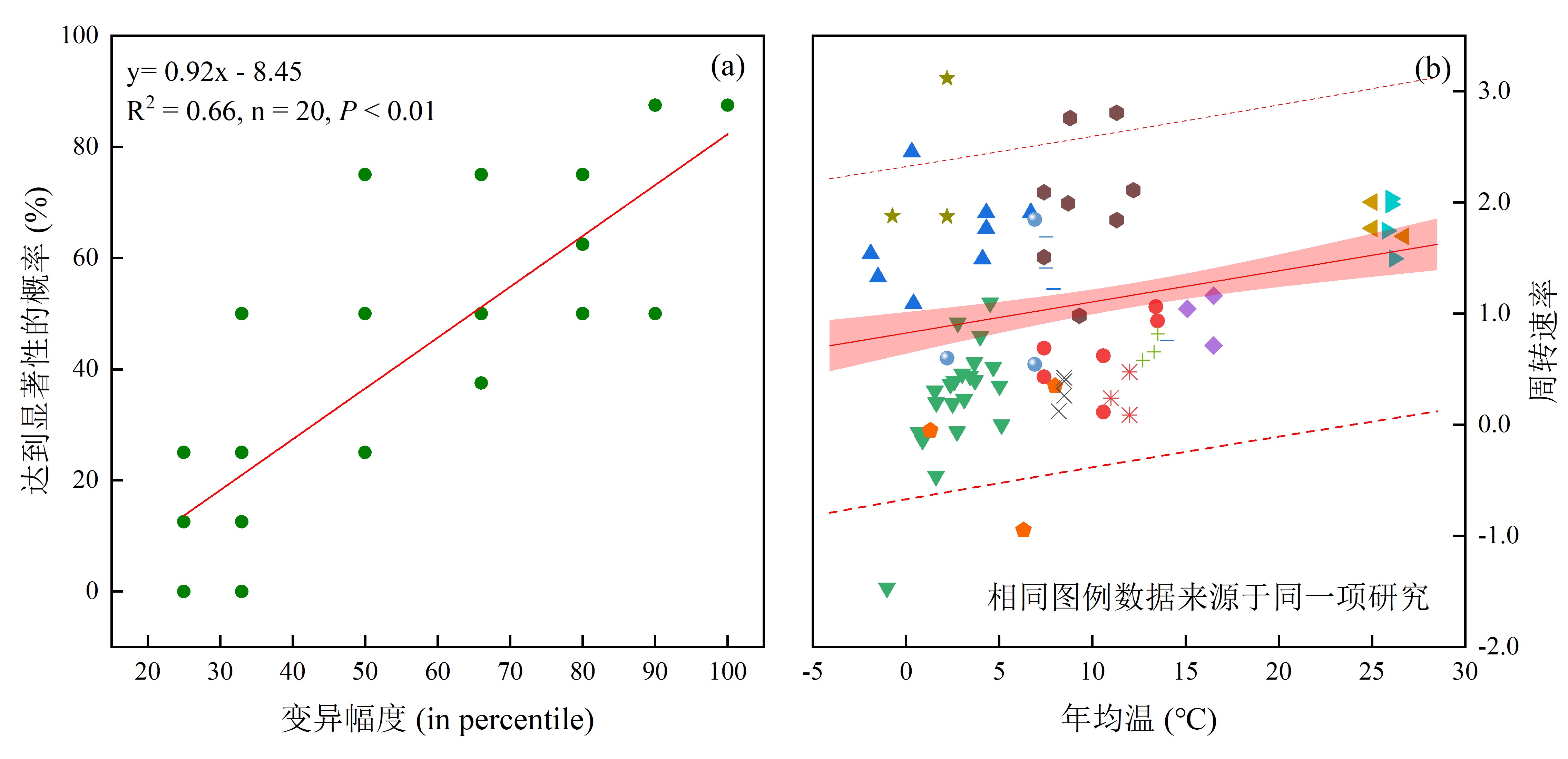 图1. 数据变异范围对统计结果的影响.
图1. 数据变异范围对统计结果的影响.
(2)因子共线性的影响:在多因子体系中,变量之间往往不是完全正交独立的,而是存在着复杂的共线性。这些共线性可能会导致表观统计结果放大、降低、抵消、甚至是逆转某一因子对因变量的真实影响。上述表现形式在不同研究中可能会有差别,具体决定于研究体系内各因子之间共线性的方式和程度。
一个通俗点的例子。两个人分别从南、北两个方向拉同一辆车(即,负相关)。如果此时评价两人对车子移动速率的贡献,可能会出现这样一种情况:南人力气稍大于北人,表观结论会是南人是显著性因子,但消极怠工,北人没有贡献。但这一评判显然没有反应北人的贡献(尽管是反作用),同时也低估了南人的努力程度。我们还可以设想其它不同的情况,但无论如何这种负相关(共线性)都使得表观统计的评判有失公允。
一个专业点的例子。在一个较大的地理范围内,年均温度、年降水量、土壤pH、土壤有机碳、土壤质地之间存在显著的正或负相关,而且可能都对土壤有机碳的周转速率存在影响。如不能克服这些共线性的影响,表观统计结果的可信度将大打折扣。由于风化成土过程的影响,土壤pH 一般与当地年均温呈现显著负相关。与此同时,土壤pH 与年均温都与有机碳分解速率呈显著正相关。这意味着,温度本身促进有机碳的分解,又通过降低土壤pH抑制有机碳分解。如果不克服两者间共线性的影响,温度和土壤pH对有机碳分解的影响都会被低估,甚至是完全抵消(即,谁都没有显著影响)。最近,我们已经通过实际数据验证了这种可能性。上一篇文章开始的时候,我提到一篇《Nature》文章认为温度对有机碳分解没有影响。该文章中仅采用了简单的回归分析,而没有考虑温度、土壤pH与有机碳分解之间的共线性。因此,他们的“不寻常”结论很可能属于这一类对统计结果的误读。
https://blog.sciencenet.cn/blog-3486388-1302126.html
上一篇:警惕:别让对统计结果的误读误导科学研究(一)
下一篇:警惕:别让对统计结果的误读误导科学研究(三)