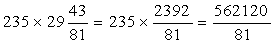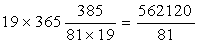《中华文明密码》-元君庙、凌家滩再考

                                                       第1部分  元君庙陶缻

                  第1节  元君庙仰韶墓地

1 中华文明的起源

中华文明在原始社会阶段，按教科书中内容可分为旧石器时代、中石器时代和新石器时代。

旧石器时代(距今约250万年-约1万年以前)，以元谋猿人（1965年在云南元谋县上那蚌村发现其化石，距今约170万年）、蓝田猿人（1963年在陕西蓝田陈家窝村附近、1964年在陕西蓝田公王岭分别发现其化石，分别距今约65万年或75-80万年）、北京猿人（1927年起在北京周口店龙骨山多次发现其化石，距今约69万年）和县猿人（1980年在安徽和县龙潭洞发现其化石，距今69万年左右）为代表，但以墓葬的形式出现的至今最早的是山顶洞人的墓葬（1930年在北京市周口店龙骨山北京人遗址顶部的山顶洞发现，约距今3.4万年至1.6万年之间），属于旧石器时代晚期。中石器时代（距今1.5万～8000年），新石器时代始于距今8000年前的人类原始氏族的繁荣时期。以磨制的石斧、石凿和石铲，琢制的磨盘和打制的石锤、石片、石器为主要工具。

陶器出现于新石器时代，是先人把粘土加水混和后，制成各种器物，干燥后经火焙烧，产生质的变化而形成的产物，可当日用品使用。仰韶文化 (西元前5000年-前3000年 )、大溪文化 ( 西元前4400年-前3300年 )、大汶口文化 ( 西元前4100年-前2600年 )是新石器时代中，墓葬文化的代表。在这3大文化中，墓中的随葬品中均有陶器发现。

仰韶文化是黄河中游地区重要的新石器时代文化，于1921年在河南省三门峡市渑池县仰韶村被发现。主要分布于黄河中下游一带、以秦晋豫三省为核心的中原地区，陕西大部、河南西部和山西西南的狭长地带为中心，东至河北中部，南达汉水中上游，西及甘肃洮河流域，北抵内蒙古河套地区。仰韶时期的人们过着定居生活，拥有一定规模和布局的村落；农业为主要经济形式，同时兼营畜牧、渔猎和采集；主要的生产工具是磨制石器；生活用具主要是陶器；埋葬制度也已经初步形成。

1931年梁思永先生与史语所同仁李济、董作宾、吴金鼎、刘耀等先生进行河南安阳殷墟发掘，发现后岗遗址的文化堆积层分三层：上层属于小屯殷商文化遗存，中层是龙山的黑陶，下层是仰韶彩陶。这三层依次相叠的堆积，明确了仰韶文化早于龙山文化，龙山文化又早于商代文化的年代关系，这就是著名的“后岗三叠层”，从地层上证明了中华文明从史前至商代是一脉相承的，从而明确了仰韶文化的相对年代约为西元前5000至西元前3000年。

2 元君庙仰韶墓地

 1958年北京大学历史系考古专业为配合黄河水库工程，组成了黄河水库考古工作队陕西分队华县队，从1958年秋至1959年秋在华县、渭南两地进行了考古工作，元君庙仰韶墓地，位于陕西省华县元君庙，南依秦岭，北有渭水流过，西南距泉护村1公里，西侧50米处有注入渭水的沟峪河。根据陪葬物，墓葬制度和墓地的排列，以及1972年中国科学院考古研究室公布的放射性碳素测定年代的数据，元君庙仰韶墓地属于中国黄河中游新石器时代仰韶文化的半坡类型墓地，半坡类型又分老官台文化、半坡类型和庙底沟类型，元君庙墓地在老官台文化（西元前6000年-西元前3000年）之后，庙底沟类型（西元前4005年-西元前2780年）之前的一种文化遗存（北京大学历史系考古教研室《元君庙仰韶墓地》文物出版社，1983年4月，p.49）。

“元君庙墓地共发掘出 51座墓葬，其中45座墓葬颇有规律地排列成6排”。著名考古学家张忠培先生（后曾任故宫博物院院长、中国考古学会理事长）发现尖底瓶存在一定的形态差别，弦纹罐数量多，而且形态有区别。在一些墓葬里，尖底瓶和弦纹罐共出；随葬尖底瓶、弦纹罐的墓葬之间存在叠压、打破关系。根据尖底瓶、弦纹罐的形式变化和组合关系，张忠培先生把元君庙墓葬分为三期。“当把墓葬分期结果放到墓地平面图里时，他惊奇地发现，自东向西的第一排、第二排、第三排依次是一期墓、二期墓、三期墓，第四排、第五排、第六排又重复这种似乎成规律的现象，整个墓地明显可以分为东、西两个墓区”（陈雍< 破译元君庙墓地“密码” — 一案边脞语之五十三>，今晚网-今晚报(天津)，2014年10月26日）。

在1983年北京大学历史系考古教研室出版了《元君庙仰韶墓地》一书中，作者把东、西两个墓区分为甲氏族墓地与乙氏族墓地，葬于甲氏族墓地的有99人，分别在24座墓葬中；葬于乙氏族墓地的有110人，分别在20座墓葬中。甲氏族墓地有7座空墓，且墓葬有单人墓和合葬墓，有1次墓葬以及2次墓葬（并非死后直接埋葬，而是经过处理后再重新埋葬），安葬的原则是：自左而右，自上而下（或自北而南，自东而西）依先后顺序墓葬。

第2节 元君庙陶缽

1  陶缽（M413:5）

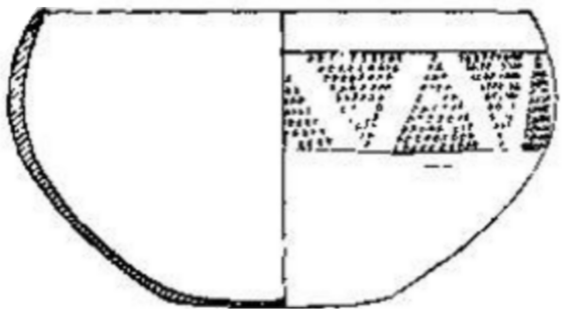
在《元君庙仰韶墓地》中，提及其中标号为M413:5的陶缽，M413墓为双人墓1次葬（墓主为男性，年龄1号骨架为25岁；2号骨架为30岁，同墓中随葬品7件），属第2期墓，位置在墓地第4排的左起第8墓穴（或右起第4墓穴）。“ⅠAC式：仅M413:5一件（图一三:6，图版一六:六）。敛口，曲鼓腹，平底。绕器壁饰椎刺的三角形纹带。三角形上下交错配置，三角形高度就是带纹的宽度。从口沿下留存的一阴线刻痕窥知，在锥刺三角形前，先绕器壁划出上下平行的两条规线，以定三角形之高亦即带纹的宽度。在这样一个半球形的器面上要划出平行的两个圆周并非易事。引人注目的是陶工在装饰三角行纹带前，曾对三角行的大小和间距在器面上的展开长度进行了较精确的计算。现存的三角形纹带已部分残损，但还剩下十个三角形。按自左至右顺序，一、二和四～十这九个三角形的面积等大，宽端为5厘米，配置等距离锥刺点十个。由宽端往上逐层减少锥刺点一个，十层至尖端仅存一个锥刺点。这九个三角形及第三、四两个三角形之间的间距相等，都是1.5厘米。第三个三角形是正置的，底边宽3.8厘米，配有九个锥刺点。该三角形也只有九层，由底部往上如积木式地逐层减少一个锥刺点，至顶端仅余锥刺点一个。二、三两个三角形的间距，也区别其他三角形之间距，上为1.8、下为1.2厘米。可以看出，第三个三角纹和其它三角纹不同，以及二、三两个三角纹间距较其它三角纹间距为小，当是设计上出现的一点误差”（北京大学历史系考古教研室《元君庙仰韶墓地》文物出版社，1983年4月，p.32-34）。

图1-1   陶缽（M413:5）形状

资料来源：北京大学历史系考古教研室《元君庙仰韶墓地》，p.33。

 2 陶缽的计算

当考古学者认为M413:5陶缽（以下简称：陶缻）第3个三角形的9数“当是设计上出现的一点误差”时，通过以下图形的锥刺点计算，发现不是误差的问题，而是当时的先人已经具有高度的数学知识。如果将三角形每层分拆，每个三角形由十层组成，根据图1-1的排列，可以得出图1-2的连续图形。以层次为纵轴，三角形的组合数为横轴，每组三角形为10层，唯独第3个三角形为底部9数，层数9数。计算结果得到表1-1三角形组合的每层合计数，发现第3个三角形底层为9个锥刺，共9层不是设计上的误差，而是显示了高度的数学水准。

                              图1-2 三角形组合

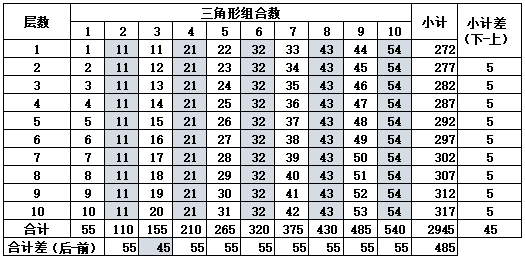
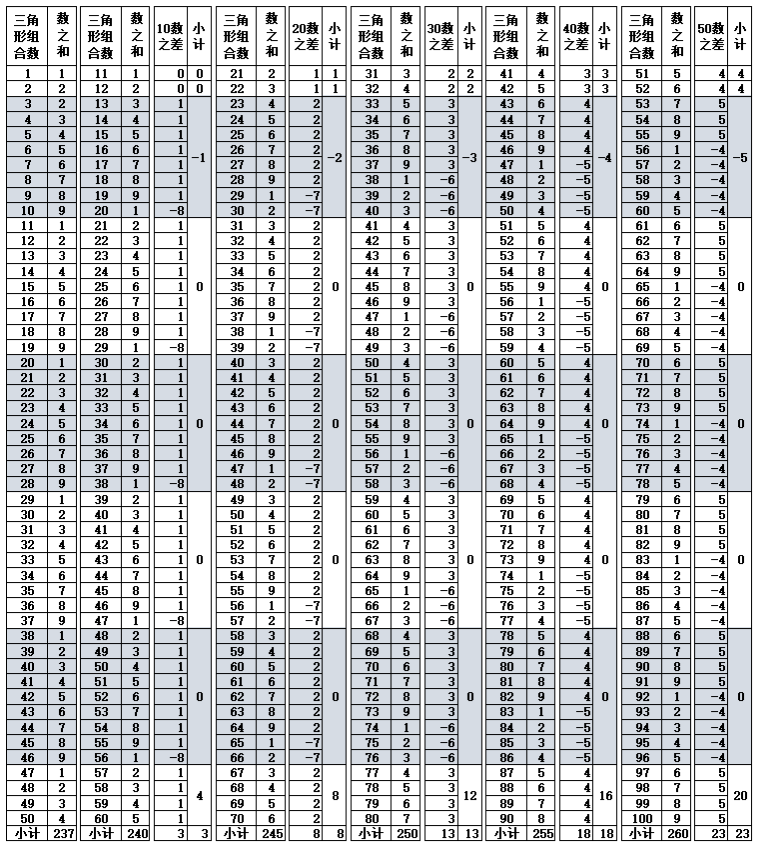
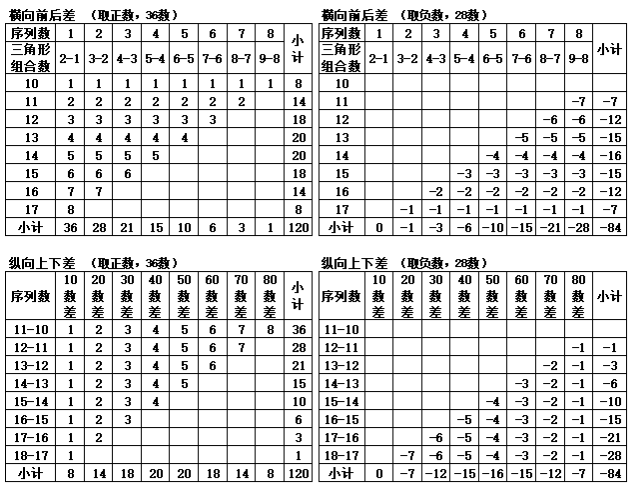
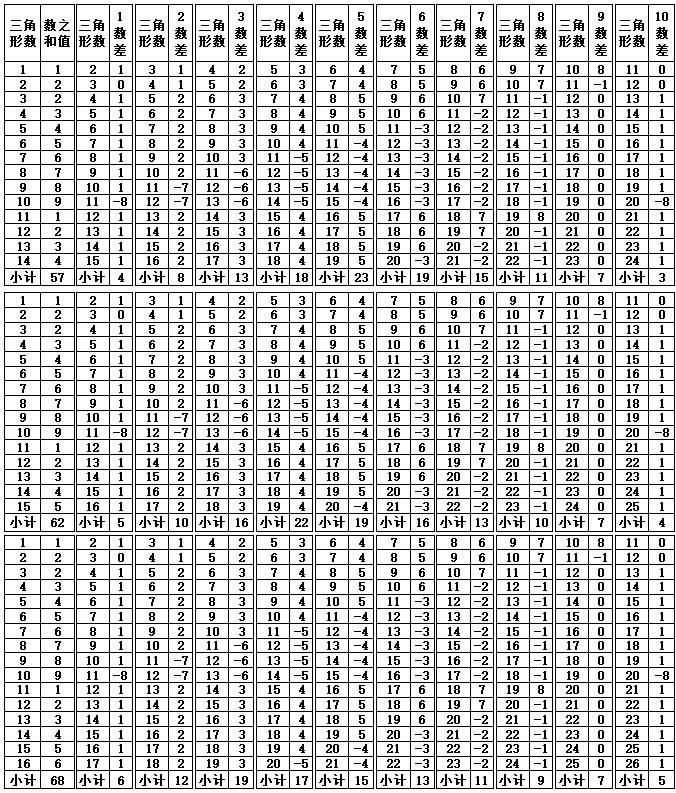
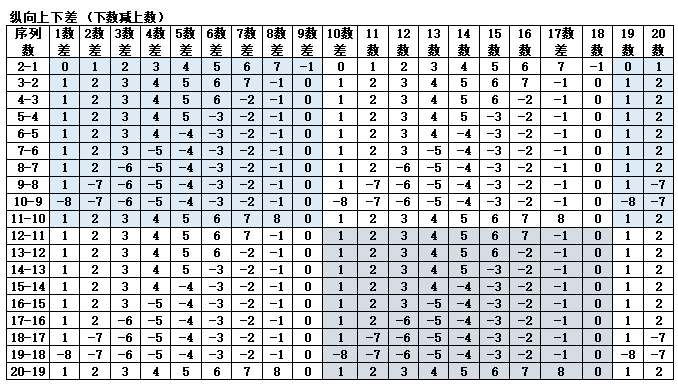
表1-1 每个层次的锥刺数统计

           注：以每一个锥刺点为1值进行统计。合计差指前后三角形的合计数差值。小计差为上下值差。

从表1-1可以明确看到，因为第3个三角形底数为9，层数为9，只要其他的三角形底数均为10，层数为10，其结果是所有的偶数三角形的层数值可以在相同的组合中得到一致的结果，即{2,4,6,8,10}5个组合的三角形每一个层数值各自是{11,21,32,43,54}，按后数减前数，差值为{10,11,11,11}(合计值43）。对应的奇数组合，根据层数的增加而增加，永远保持递增的趋势，即{1,3,5,7,9}5个组合的三角形合计值各自为{55,155,265,375,485}，按后数减前数，差值为{100,110,110,110}(合计值430），按平均值计算{10,11,11,11}与偶数的单位数值相同。由此可以看到第3个三角形底数为9，层数为9的设计，体现出中华文明中的“3、6、9”概念中，其中的3和9的重要性。同时，第6个三角形每层的数值是32，数之和值为5（3+2=5），一般每个三角形按底数10、层数10计算锥刺点，合计数为55点，第3个三角形底数为9，层数为9，锥刺点合计数为45，55+45=100，55-45=10，100为10数的10倍（10的2次方），若将第2和第3三角形组合，如图1-3所示，每一层的合计数均为10，总数100。

                              图1-3  第2、3三角形组合

如果把奇数代表阳（男性）；偶数代表阴（女性），用今天的人体性染色体的知识去理解，男性的性染色体由XY组成，女性的性染色体由XX组成，那么表1-1的规律代表着女性的性染色体比较男性的要稳定，佐证了在新石器时代尚处于母系社会情况下，该理论在当时得到先人的认可。且这理论在天文历法中，将被运用到对太阴（月亮）的观察，因为太阴（月亮）的变化规律相较与太阳的运动变化，其稳定性大，28星宿的概念应该与此理论有关。

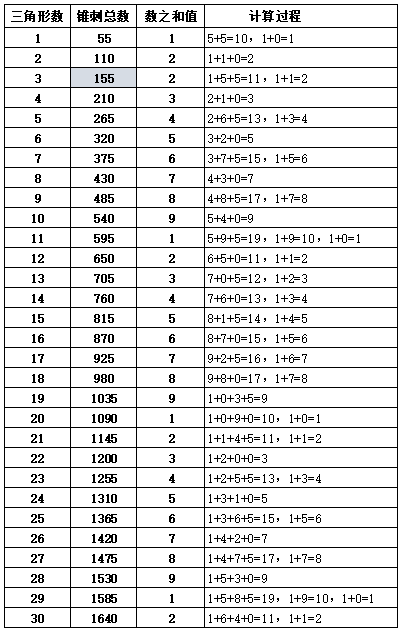
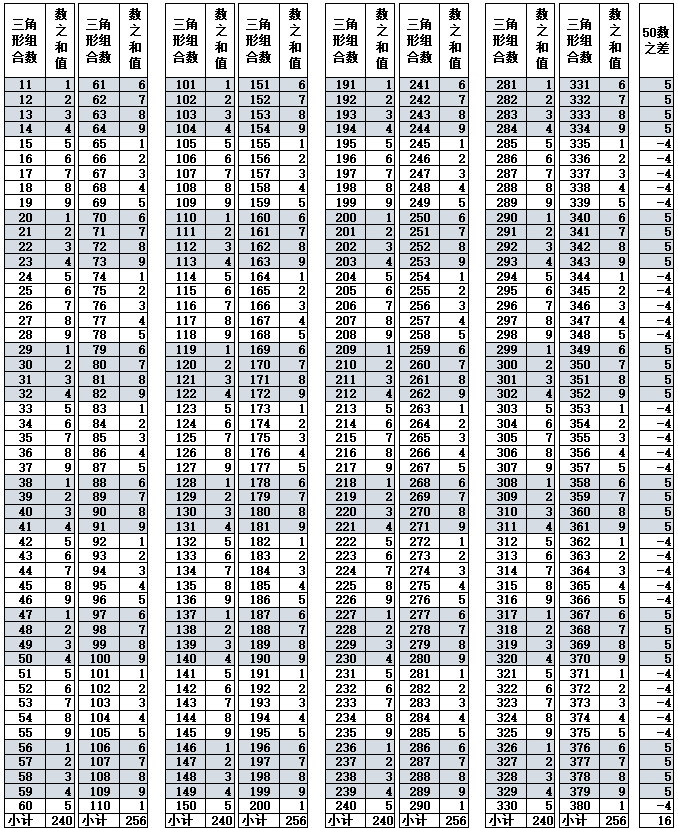
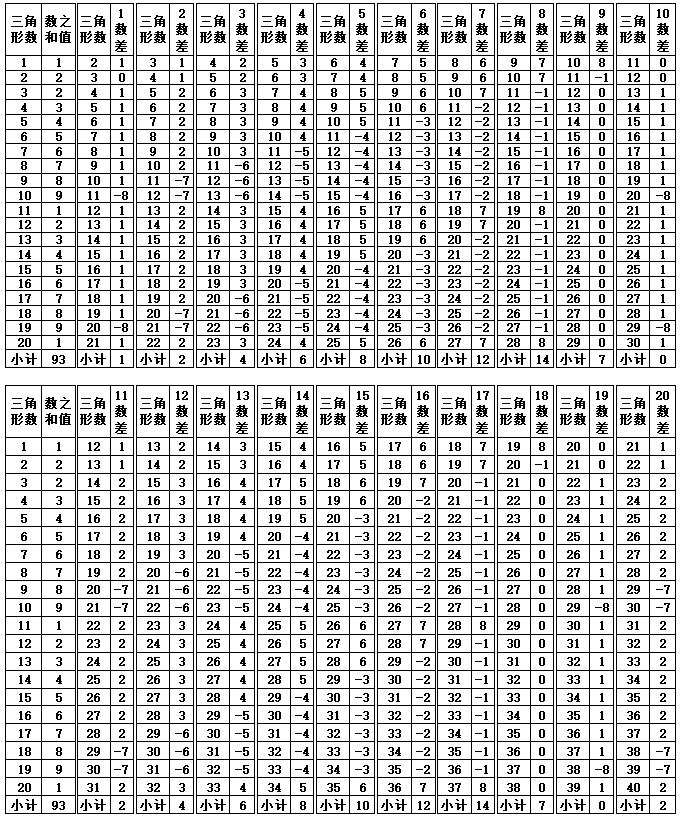
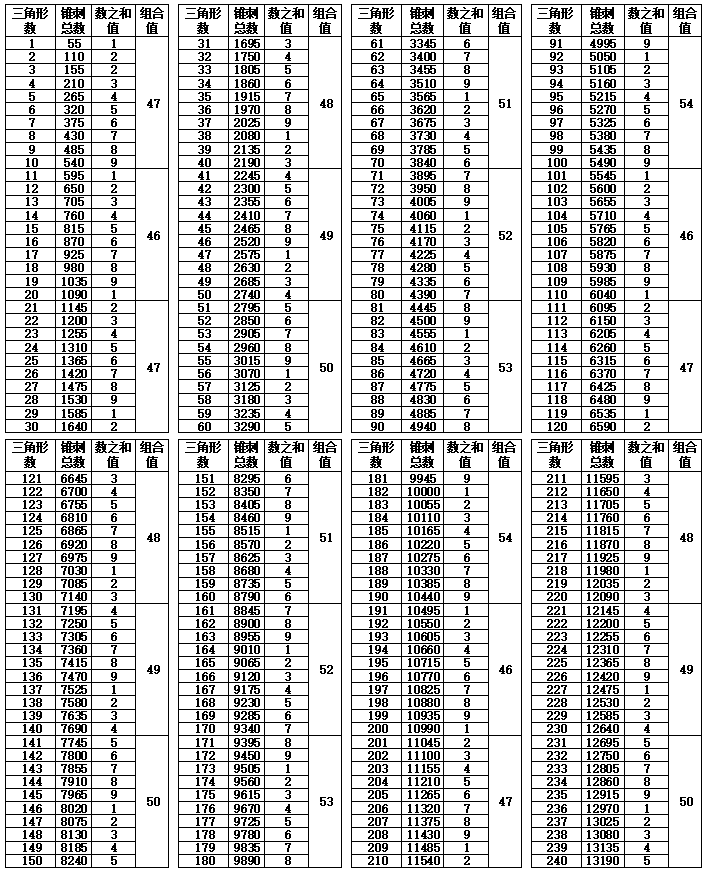
假设如图1-3，把第3个三角形的10层次从上至下理解为是{0,1,2,3,4,5,6,7,8,9}的话，也可以认为，在当时“0”（零）的概念已经存在，“9”与长久、持久的“久”同音，因此“9”代表了最高数的概念就能理解。虽然当时还没有文字的出现，但锥刺点的记录已经明确告诉后人，世界是有规律的，该图形非常之完美。表1-2，对三角形的锥刺总数进行数之和计算，个位数不变，十位数除以10，百位数除以100，依次类推，锥刺总数均当个位数相加，如出现2位以上的数值再次当个位数相加，其结果，除第3个三角形不是顺序数以外，其他所有的数之和值都完美的按照1-9的顺序排列，并且循环。

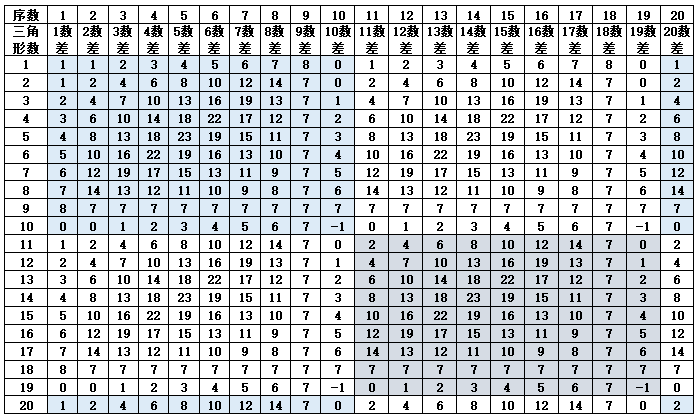
  表1-2  三角形锥刺总数的数之和值

             注：第3三角形按45数计算，其他均为55数。

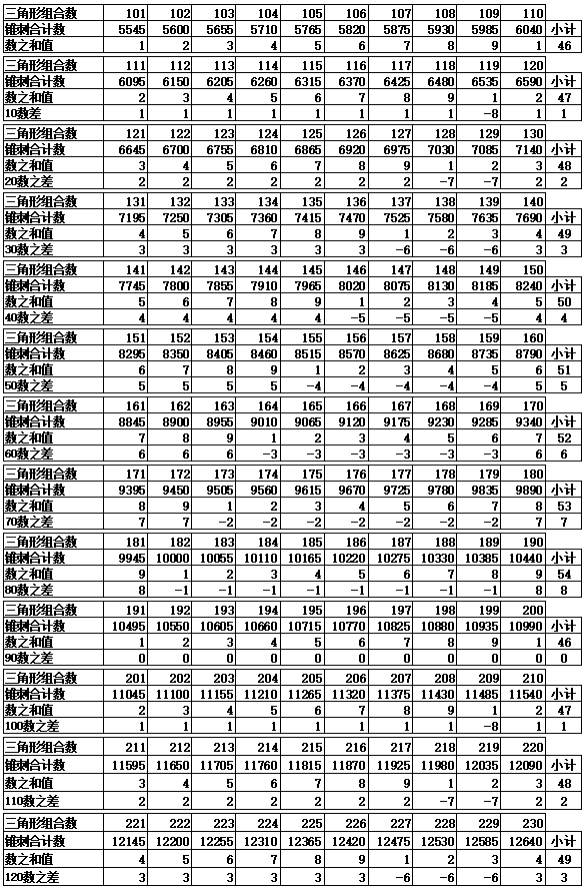
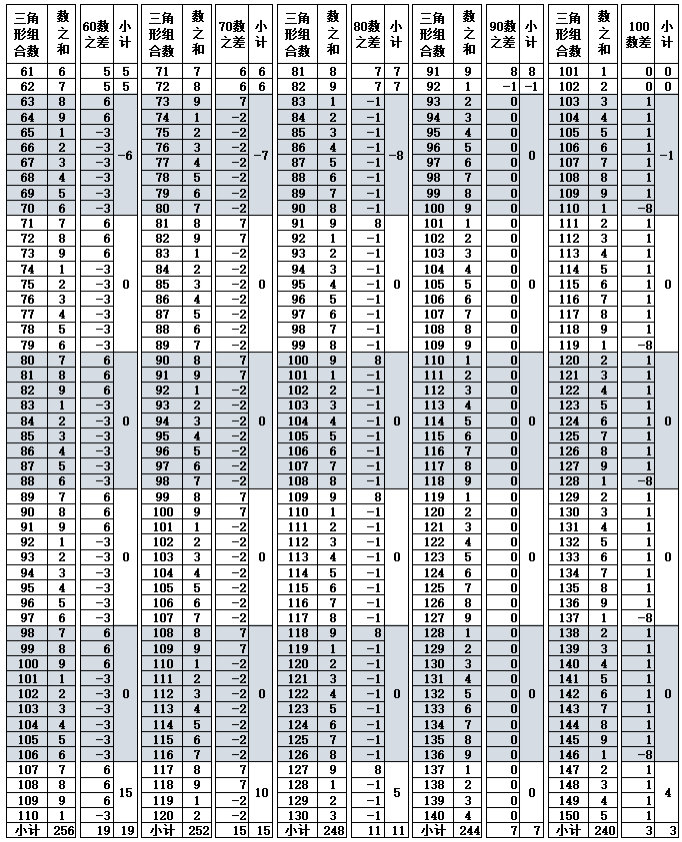
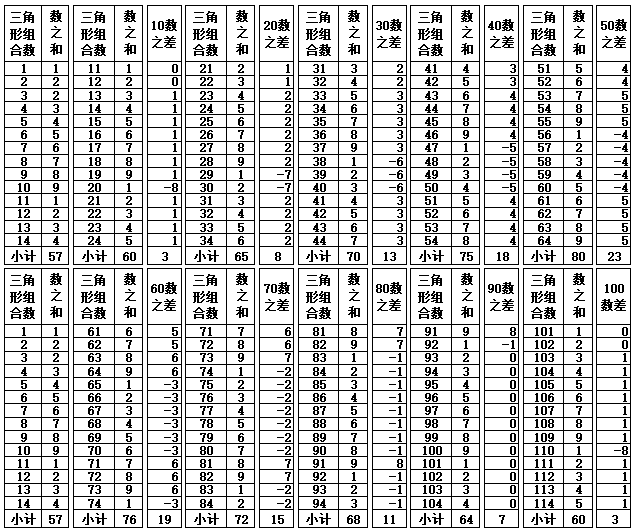
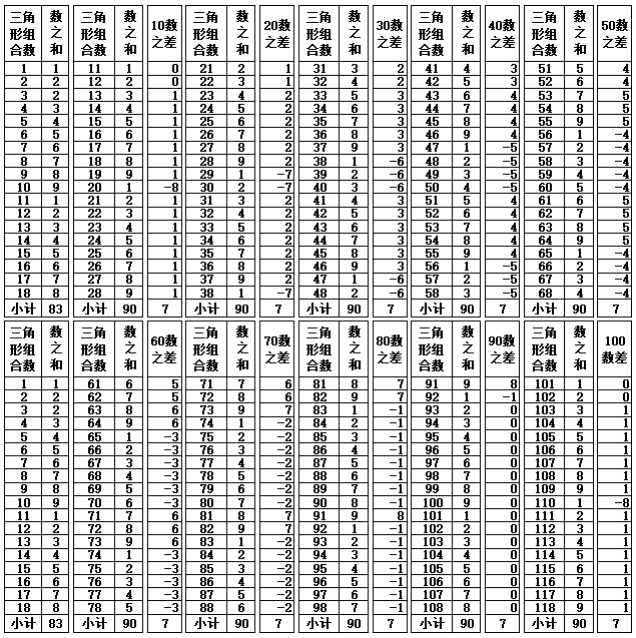
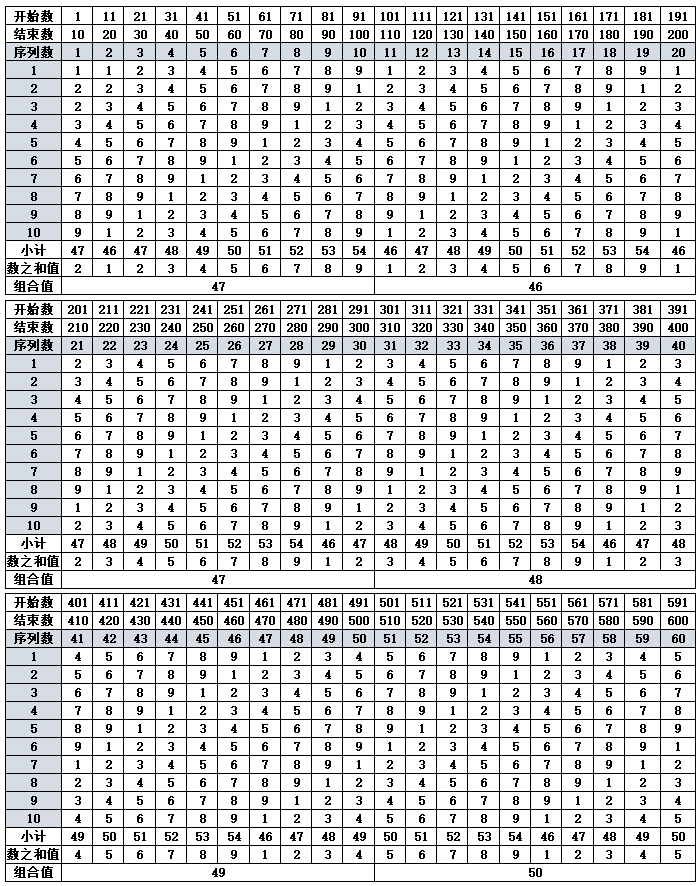
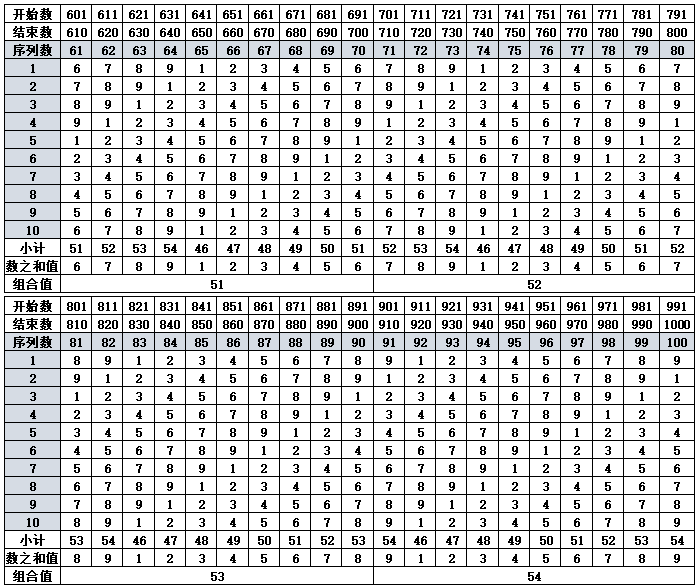
根据表1-2数之和值具有循环变化的规律，11-19三角形组合数的末尾个位数与数之和相等，第20个三角形的数字开始不再对应，以后再要对应，要到101-109个三角形组合数的末尾个位数时，与数之和值的数字匹配，所以表3从101个三角形的组合开始计算，假设1个三角形的锥刺合计数为55，n个三角形组合的锥刺数就是{55×(n-1)+45,n≧3}，并且以101-110个三角形组合数为标准基数，每增加10个组合数进行一次差值检验，发现每递增每10个三角形组合数的变化如下（注：@代表出现的数字，*后面代表出现的次数）：

10数之差的差值变化是{1,1,1,1,1,1,1,1,-8,1}（@1*9-@8*1=1）；

20数之差的差值变化是{2,2,2,2,2,2,2,-7,-7,2}（@2*8-@7*2=2）；

30数之差的差值变化是{3,3,3,3,3,3,-6,-6,-6,3}（@3*7-@6*3=3）；

40数之差的差值变化是{4,4,4,4,4,-5,-5,-5,-5,4}（@4*6-@5*4=4）；

50数之差的差值变化是{5,5,5,5,-4,-4,-4,-4,-4,5}（@5*5-@4*5=5）；

60数之差的差值变化是{6,6,6,-3,-3,-3,-3,-3,-3,6}（@6*4-@3*6=6）；

70数之差的差值变化是{7,7,-2,-2,-2,-2,-2,-2,-2,7}（@7*3-@2*7=7）；

80数之差的差值变化是{8,-1,-1,-1,-1,-1,-1,-1,-1,8}（@8*2-@1*8=8）；

90数之差的差值变化是{0,0,0,0,0,0,0,0,0,0}（@0*10=0）；

100数之差的差值变化是{1,1,1,1,1,1,1,1,-8,1}（@1*9-@8*1=1）；

110数之差的差值变化是{2,2,2,2,2,2,2,-7,-7,2}（@2*8-@7*2=2）；

120数之差的差值变化是{3,3,3,3,3,3,-6,-6,-6,3}（@3*7-@6*3=3）。

以此类推，以上是以90数差为一个周期发生变化，而且是有规律地循环发生。

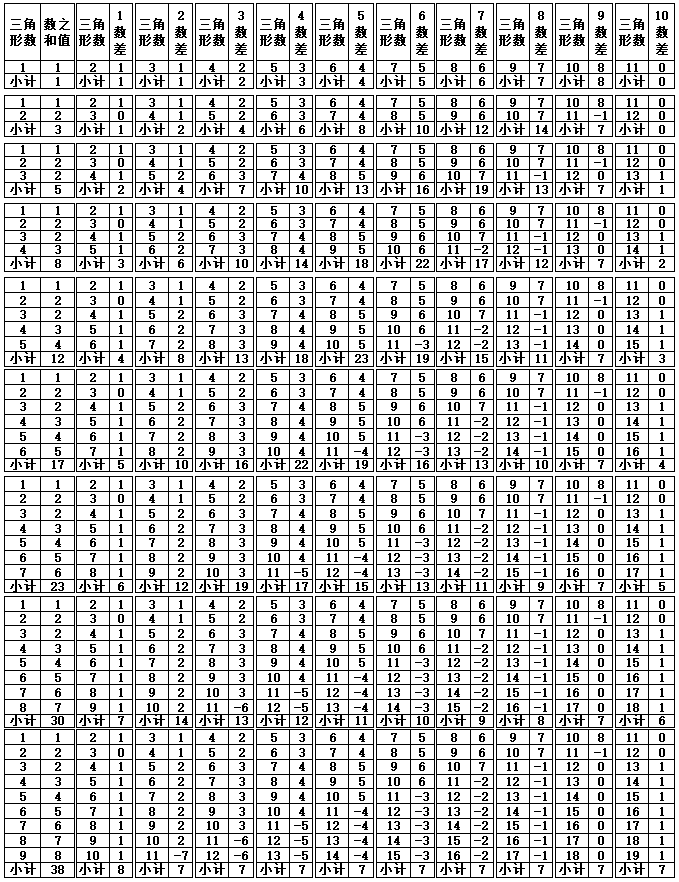
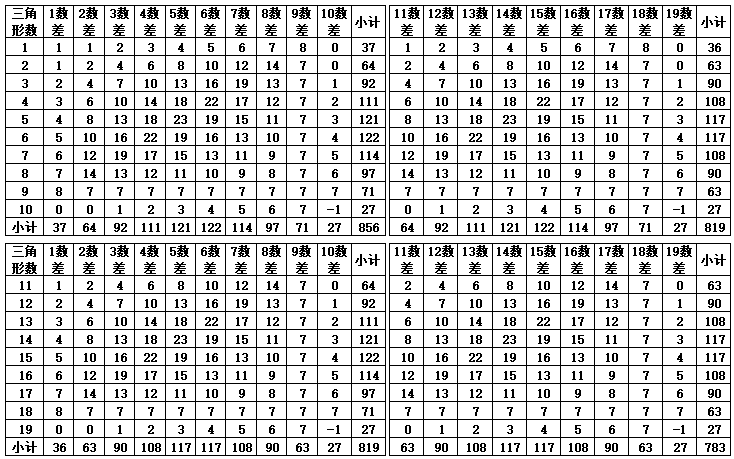
  表1-3 数之和的差值变化（第101-230个三角形数）

 根据表1-2、表1-3计算出三角形的组合数的数之和值，可以发现，如果取前10个三角形的数据，{1,2,2,3,4,5,6,7,8,9}(合计值47），此外除前10个三角形之外的数之和值之间的数差并不需要特定的数字作为基准，只要排除前10个三角形的数据，后续的其他的数字差不管是从那个数字算起，差1、10，100，1000…，只要数之和的差值个数一致，差值的结果就一致。如差值数差2，20，200…，最后的结果也等同于差值2的变化。其他同理可得，且从前9个数至后9个数的数之和值变化会重复出现，在10～80的个数变化范围内，正负差值总合计数为“36”{1,2,3,4,5,6,7,8}，第90个数的差值均为“0”（零）值。表1-3中，第100-120的数之和值差值产生的{1,2,3}差值与第10-30的数之和值差值产生的{1,2,3}差值结果相同，可重复出现。

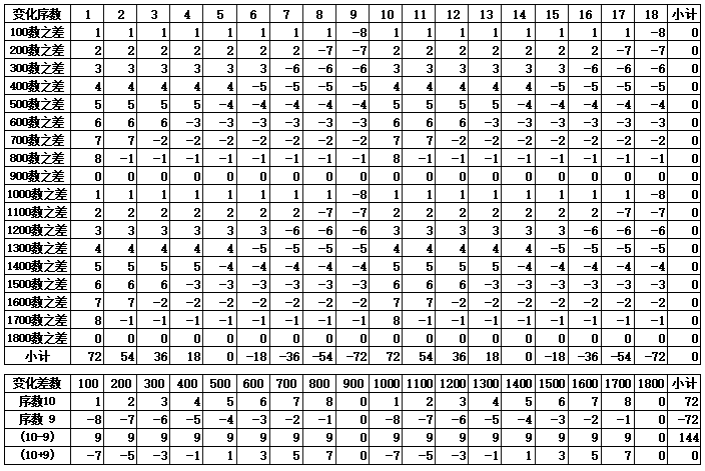
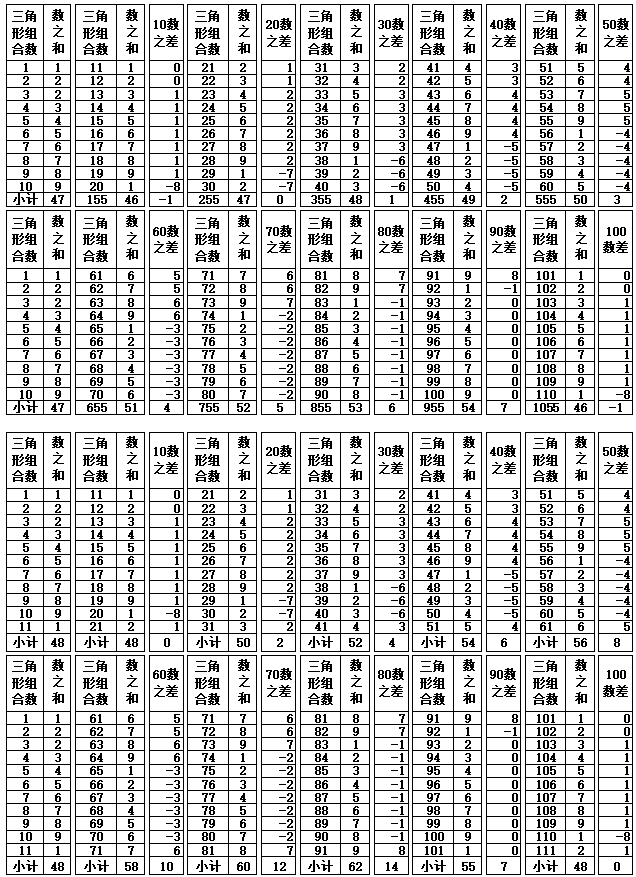
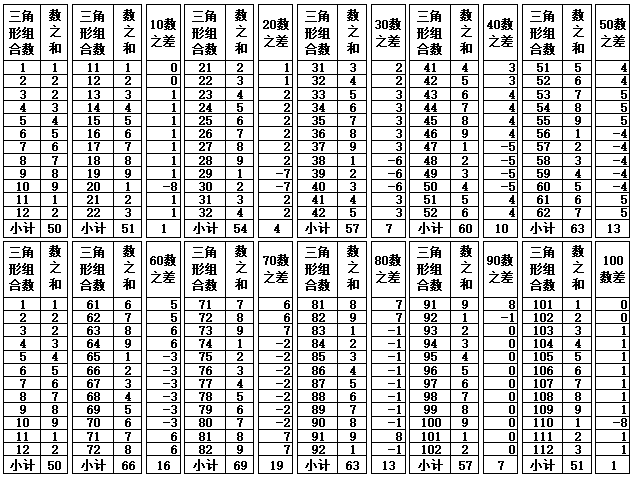
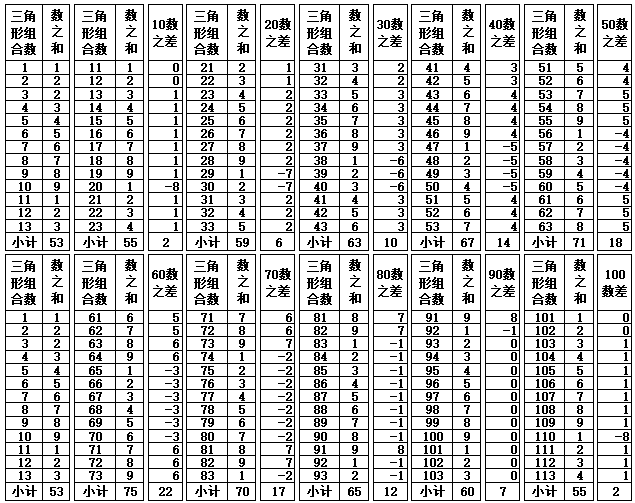
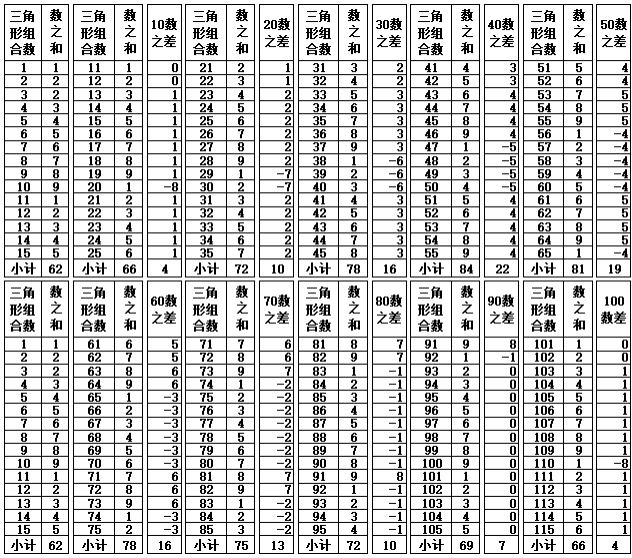
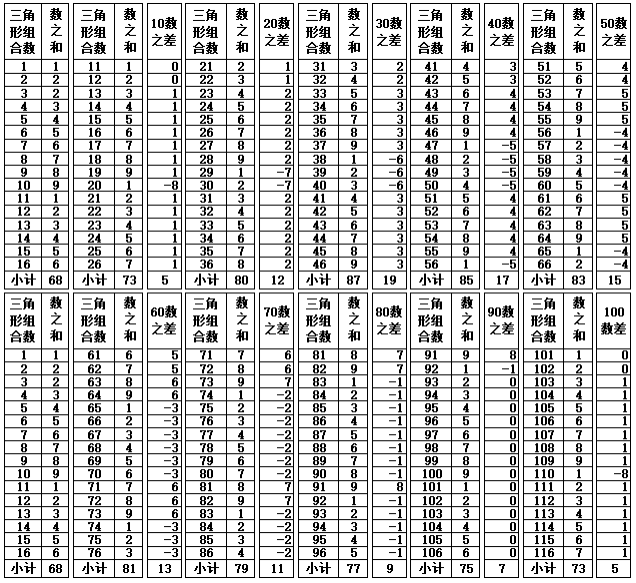
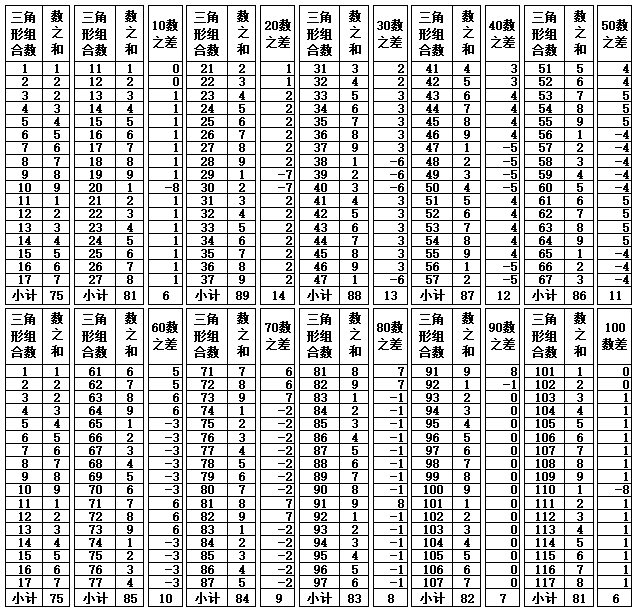
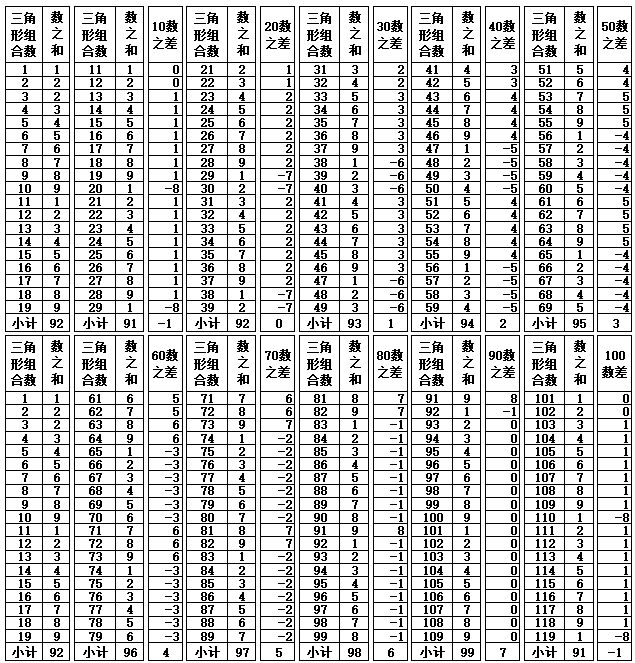
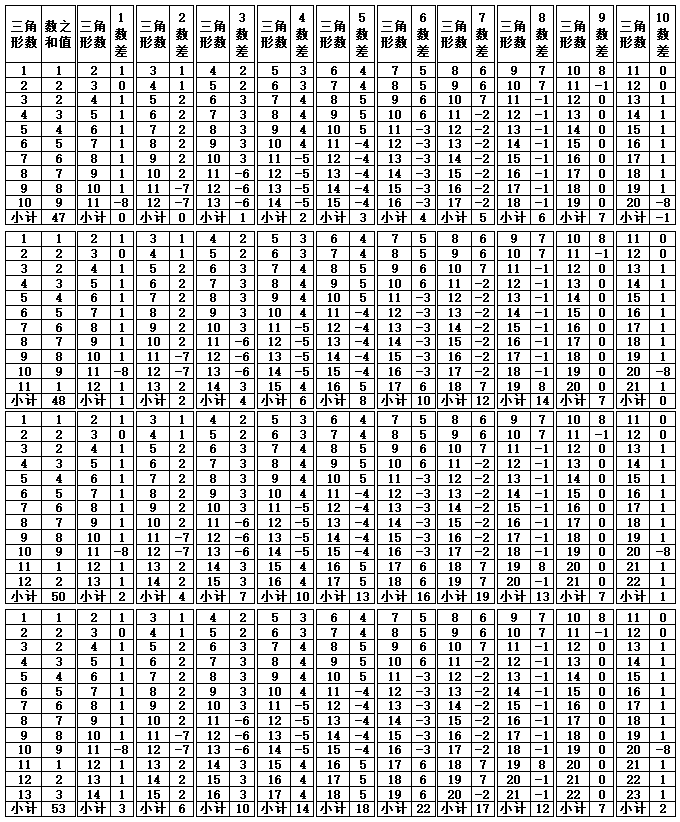
表1-4 数之和的差值变化（第101-1801个三角形数）

表1-4的100-1800数之差，如果以变化序数1-9数为一个单元，变化序数10-18数为第2个单元，可以看到每一单元的变化规律同样是循环发生变化。具体如下：

100数之差的差值变化是{1,1,1,1,1,1,1,1,-8}（@1*8-@8*1=0）；

200数之差的差值变化是{2,2,2,2,2,2,2,-7,-7}（@2*7-@7*2=0）；

300数之差的差值变化是{3,3,3,3,3,3,-6,-6,-6}（@3*6-@6*3=0）；

400数之差的差值变化是{4,4,4,4,4,-5,-5,-5,-5}（@4*5-@5*4=0）；

500数之差的差值变化是{5,5,5,5,-4,-4,-4,-4,-4}（@5*4-@4*5=0）；

600数之差的差值变化是{6,6,6,-3,-3,-3,-3,-3,-3}（@6*3-@3*6=0）；

700数之差的差值变化是{7,7,-2,-2,-2,-2,-2,-2,-2}（@7*2-@2*7=0）；

800数之差的差值变化是{8,-1,-1,-1,-1,-1,-1,-1,-1}（@8*1-@1*8=0）；

900数之差的差值变化是{0,0,0,0,0,0,0,0,0}（@0*9=0）；

1000数之差的差值变化是{1,1,1,1,1,1,1,1,-8}（@1*8-@8*1=0）；

以此类推，100-900数之差与1000-1800数之差，同样是一个大循环。每900数差为一个大单元。如果以100-1800数差为一个大组合，变化序数1-9数（或变化序数10-18数）的9个组合合计为“0”（零），取正数值{72,54,36,18},合计180数，平均45数（180/4=45）。如果以100-900数差为一个小组合，则正数合计值为{36,27,18,9},合计90数，平均22.5数（90/4=22.5），四舍五入取整数，为“23”数，如不保留小数取整数，为“22”数。

表1-4中，变化序数10与变化序数9的差值合计为“144”（@9*16=144），这里还看不出有什么具体意义。将在以后章节中具体阐述其意义所在，但可以明确一点，从第1单元过度到第2单元，变化序数（10-9）的差值均为“9”数，2个组合差共出现16个“9”数，100-900的单元（或1000-1800单元）中，各有8个“9”数，代表着如果可循环可持久，差值均为“9”数，一个循环72数（144/2=8×9=72）；但如果做加法，变化序数（10+9）的合计数为“0”（零），不可循环，将归为“0”（零），因此，每次循环的交接点就变得非常重要，必须关注。在天文历法中，“冬至日”就有其特别的重要性。加法中产生正数值{1,3,5,7}(合计16），100-1800数差为一个大组合，其中有2个{1,3,5,7}，合计值为32。

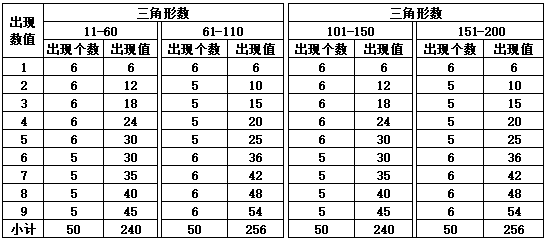
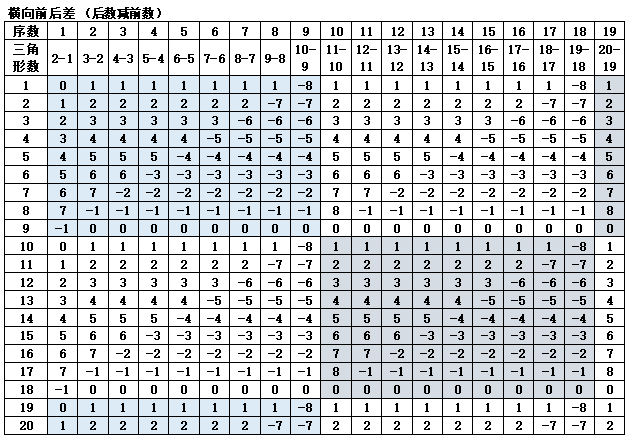
          表1-5 三角形每50数差的变化(第11个三角形组合之后的差） 

表1-5计算了三角形组合数每差50数的情况下，第61与第11的数之和之差、第151与第101的数之和之差、第241与第191以及第331与第281的数之和之差，只要差50个三角形数，都会出现50数之差的差值变化是{5,5,5,5,-4,-4,-4,-4,-4}（@5*4-@4*5=0）的循环，与其他数字的9数差值规律一致，只是表现的数值不同。

  表1-5中另一个规律是，三角形组合数的差值有5数与4数两种情况，5数差对应的数之和值有{1&6,2&7,3&8,4&9}4个组合情况重复出现。这规律与第2章的河图洛书的图形有关。而4数差对应的数之和值有{1&5,2&6,3&7,4&8,5&9}5个组合重复出现。

{1&6,2&7,3&8,4&9}的8数合计值为40（1+2+3+4+6+7+8+9=40）；{1&5,2&6,3&7,4&8,5&9}10数合计值为50（1+2+3+4+6+7+8+9+5×2=50）。@40×5=@50×4=200；@8×5=@10×4=40，200/40=5，18×5=90=50+40。故2个9数组合18个数之和值绝对值可得合计数“90”。

取100个差值，前50个值的合计数为240数，后50个值得合计数为256数，差16数。如果把每50个数两两相减，同样可以得到24个5数差和26个4数差（@5*24-@4*26=16）。此外，前50个数的合计数之和值为240，后50个数的合计数之和值为256，前后50个数值中，出现的数之和值“1”数各有6次，其余8数以{2,3,4,5}、{6,7,8,9}为2个组合，在合计数“240”中，{2,3,4,5}（合计14）出现5次、{6,7,8,9}（合计30）出现6次，故240=@1×6+@14×6+@30×5=6+84+150，{6,84,150}的数之和1值为{6,12,6},合计24数；数之和终值为{6,3,6},合计15数，15、24与240的数之和终值均为“6”。合计数“256”中{2,3,4,5}为6次、{6,7,8,9}为5次，故256=@1×6+@14×5+@30×6=6+70+180。{6,70,180}是数之和终值为{6,7,9},合计22数，22与256的数之和终值均为“4”。故240+256=496，数之和1值为“19”（4+9+6=19），终值为“1”（1+9=10，1+0=1）。

因此，如果以每100个数为统计对象（@1×12+@8×11=12+88=100），数之和总值496数为一个大单元，1数的出现次数为12次，出现值为“12”，其他{2,3,4,5,6,7,8,9}8数共出现11次，{（2+3+4+5）+（6+7+8+9）}×11=(14+30)×11=484，共计496（484+12=496），且前50个值的合计数与后50个值的合计数差值为“16”。496/16=31，{496,31,16}的数之和1值分别为{19,4,7},{496,31,16}的数之和终值各为{1,4,7}，496=1+55×9，16=7+1×9，故496为数之和“1”值的第56位（1+55=56），16为数之和“7”值的第2位（7+1×9=16，1+1=2），56/2=28；4×7=28，似乎与28星宿的理论有关联性。

以上的50数差以第11个三角形之后的50数为差值计算，可知分类结果有2个大类。但是，陶缽设计的10个三角形基数也需考虑，即考虑第3三角形的特殊性。

    表1-6 三角形10-100数差的变化(第1-50个三角形组合为基准）

表1-6以第1-50陶缽三角形为基数，按10-100个三角形的数之和值进行差值计算，其结果10数至90数差是一个大循环，100数差值与10数差值的结果相同。如以10个组合值进行差值计算，后数减去前数，前4个组合差值均为5数，后5个组合差值均为4数，故如可循环，10个组合产生的9个差值合计为“0”（零）。如果不可循环，以9个组合值进行差值计算，产生的8个差值合计为“4”数（4×@5-4×@4=4）。由此可知以陶缽设计的10个三角形组合为基准，进行差值计算具有一定的现实意义。

故表1-7以陶缽的10个三角形组合（1-10的组合数）的数之和值为基准，按10-100个三角形的数之和值进行差值计算，之后基准数以每增加一个三角形值，各自进行10-100个三角形的数之和值的差值计算，发现三角形基数为第19个数的差值结果与第10个数差值相同，说明横向差数以90数为一个循环，纵向差值以每9个三角形组合为一个循环，均以9数为循环。

        表1-7 三角形10-100数差的变化(分别以第10-19个三角形组合为基准）   

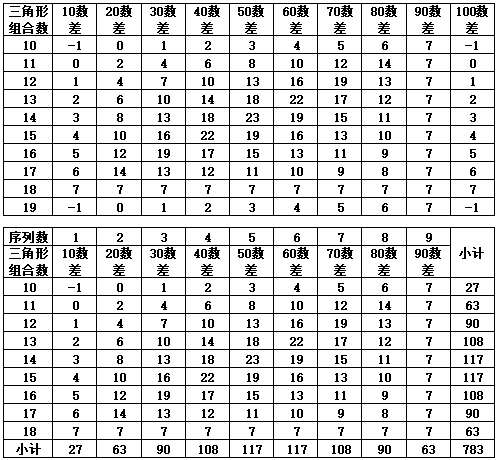
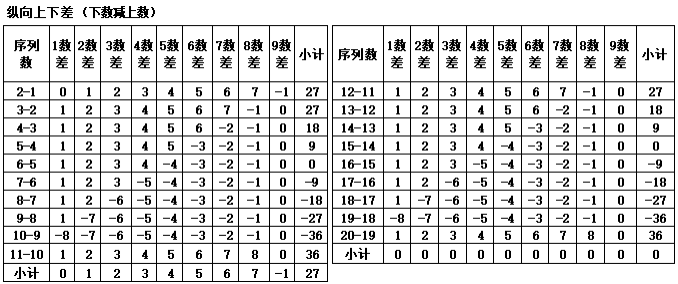
   通过表1-8的汇总，发现三角形组合数的变化以10数-18数为一个循环，差数100数与差数10数重叠，故取差数10-90数为一个循环。

           表1-8  三角形10-100数差的变化(分别以第10-19个三角形组合为基准）汇总

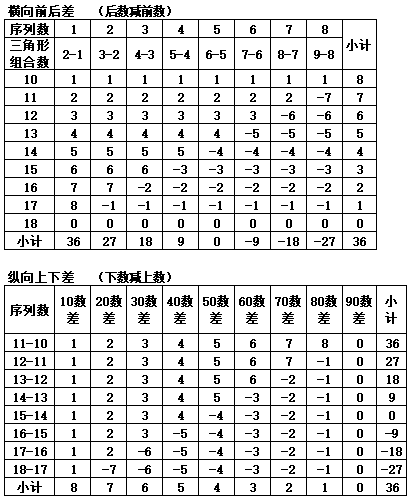
   表1-8对第10至第18个三角形组合的差值进行汇总，纵横共81数，对纵横各9数进行横向差值计算（10数差的再差值）以及纵向差值（三角形组合的再差值）计算，纵横差值除去零值（17数），余正负差值个数64数；合计值为36。并对纵横差值按正数与负数进行分类，可知纵横差值的正数各为36数，合计值各为“120”；负数各为28数，合计值为“-84”，代表9纵9横进行差值计算，无论是纵向还是横向进行差值计算，除去零值，均可以得到8纵8横的差值结果。且差值合计数的结果一致。但如果以各自出现的差值个数看，横向差值的横向小计值从上往下为{8,7,6,5,4,3,2,1}，合计36；纵向差值的小计值从左至右为{8,7,6,5,4,3,2,1}。如取正数，横向的从上往下的小计值为{8,14,18,20,20,18,14,8}，合计“120”；取负数，从上往下的小计值为{-7,-12,-15,-16,-15,-12,-7}，合计“-84”数。纵向差值以从左至右与横向差值相同。

  以上表1-8的汇总中，横向差是表1-7的10数至90数的差再次进行差值计算，代表着各10数的等差结果，而纵向差是以表1-7三角形组合差再次进行差值计算，代表着每增加一个三角形组合的差值计算。其8纵8横的纵横64数的正数结果36数，合计值120，如果按1-8数统计，120/8=15，目前尚不知有什么具体意义，但与陶缽的三角形间距15毫米有关联；而负数的28数，合计值84，如果按1-7数统计，84/7=12，是陶缽的第2与第3的底部间距12毫米的数值。从纵横的差值按正负数区分后，图形的数值非常有规律的排列。故表1-9继续计算，以20个三角形组合为基准，分别计算1数差至20数差的差值，发现1数的差值之后没有发生循环，而2数至10数与11数至19数的差值合计数相同，分别为{2,4,6,8,10,12,14,7,0}，合计值63。20数差又与2数差的合计值相同。因此，可以认为，只要计算1数至10数的结果，就可以知道之后的循环趋势。

       表1-9 三角形1-20数差的变化(20三角形组合为基准）   

  表1-10 三角形1-10数差的变化(第1-19各三角形组合为基准） 

表1-10，对表1-9的差值分别以1-20个组合为基准，观察1数-10数的差值情况，表1-11对表1-10的差值合计数进行汇总，发现纵向1-10个组合的差值小计数各自不同，从11个组合开始，与第2个组合相同，同样可以循环。11-19组合与2-10组合的差值小计数相同，这样以19数差，19个组合形成4个不同的结果。第1个方阵有100个值{10（第1-10组合）×10（第1-10数差）}；第2个方阵有90个值{9（第11-19组合）×10（第1-10数差）}；第3个方阵有90个值{10（第1-10组合）×9（第11-19数差）}；第4个方阵有81个值{9（第11-19组合）×9（第11-19数差）}，且第2个方阵与第3方阵等值，第2方阵的纵值与第3方阵横值相等，第2方阵的横值与第3方阵纵值相等，可以看作为相同数值的纵横表现，故以19数差乘以19个组合形成361个不同的结果，最终可以分类为3大类即按个数分类有{100,90,81}之分；按数值的合计数分类，可分为{856,819,783}，总计个数361数（100+90×2+81=361），总值3277（856+819×2+783=3277），3277的数之和1值为19（3+2+7+7=19）；数之和终值为“1”。{856,819,783}数之和1值分别为{19,18,18}，合计55（19+18+18=55）；数之和终值分别为{1,9,9}，合计值19。但如按{856,819,819,783}4个方阵的合计数统计，数之和终值各为{1,9,9,9},合计值28。

   表1-11 三角形1-20数差的变化(第1-20各三角形组合为基准）小计值汇总

仔细观察从三角形11-19组合产生的差值小计，11数至19数的小计值{63,90,108,117，117,108,90,63,27}合计值783，以前数减后数，得到的小计差值为{-27,-18,-9,0,9,18，27,36},合计36，如果取差值的正数，{9,18,27,36}合计90，分别是9数的{1,2,3,4}倍；而负数{-27,-18,-9}的合计为54，分别是9数的{3,2,1}倍。{63,90,108,117,117,108,90,63,27}数之和终值均为“9”,按数之和终值统计，合计值为81数（9×9=81）。1数至10数的小计数值{64,92,111,121,122,114,97,71,27}的数之和终值分别为{1,2,3,4,5,6,7,8,9},合计45。81-45=36；819-783=36，2种方式的差值相等。数值虽然众多，但实际就是1数差的三角形11-19组合的{1,2,3,4,5,6,7,8,0}的合计值36的差值结果。换言之，2-10数差与11-19数差，差值完全相同，即11-19数按数之和值1表示，就是2-10数值；如按数之和值终值表示，即1-9数值。同时，前后2个单元在数之和值层面上，与表1-2的计算结果相同，具有变与不变的结果。前10数差（1-10数差）的合计（小计值）代表变，随三角形数的增加而递增({1,2,3,4,5,6,7,8,9})，后9数差（11-19数差）的小计值代表不变，均为“9”数。

同理，从三角形1-10组合产生的差值小计值，除三角形1数组合以外，其他的数值与11-19组合的数值重复，故三角形1数组合的前10数差（1-10数差）小计37数的数之和值为“1”，后9数差（11-19差）小计36数的数之和值为“9”，11数至19数的小计值{36,63,90,108,117，117,108,90,63,27}合计值819，以前数减后数，得到的小计差值为{-27,-27,-18,-9,0,9,18，27,36},合计9，如果取差值的正数，仍然{9,18,27,36}合计90，是9数的{1,2,3,4}倍，但负数的合计数为“-81”（{-27,-27,-18,-9}），比三角形11-19组合的11数至19数的小计值大27数。所以，依然前10数差代表变化，后9数差代表不变，数之和值均为9数，合计值90（10×9=90）。1至10数的小计数值{37,64,92,111,121,22,114,97,71,27}合计值856，以前数减后数，得到的小计差值为{-27,-28,-19,-10,-1,8,17,26,44}，合计值10。{37,64,92,111,121,22,114,97,71,27}的数之和终值分别为{1,1,2,3,4,5,6,7,8,9},合计值46，90-46=44，856-819=37，44-37=7，代表着在从三角形1-10组合产生的差值小计，前10数差（1-10数差）与后9数差（11-19数差）在数之和差值结果与非数之和差值结果不一致，存在“7”数之差。

  表1-12以表1-11为计算对象，按照表1-8的形式，同样做小计值的再差值，观察到纵横差值的计算均有2种结果出现，横向差值以每9个组合9个差数为一个方阵，从第2个单元开始可以循环；而纵向差值结果，第一个单元以11个组合产生的10个差值与9数差为一个单元，纵向第2单元以10个组合产生的9个差值与9数差为一个单元，因此纵横的差值结果不同。

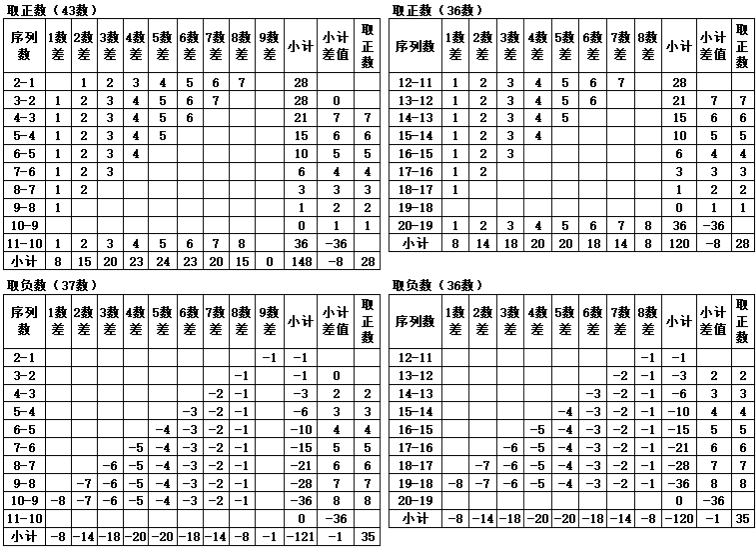
        表1-12 三角形1-20数差的再差值

     表1-13 三角形1-20数差的再差值（按正负数分类）

表1-13的纵向正数中，以{43,36}个数交替出现，各自的合计数为{148,120}。纵向的前11个三角形组合差产生的10个差值，按小计值从上往下为{28,28,21,15,10,6,3,1,0,36}，合计值148；后11-20组合差产生的9个差值按小计值从上往下为{28,21,15,10,6,3,1,0,36}，合计值120。

纵向负数中，以{37,36}个数交替出现，各自的合计数为{-121,-120}，前11个三角形组合差产生的10个差值小计，按小计值从上往下为{-1,-1,-3,-6,-10,-15,-21,-28,-36,0}，合计值“-121”；后11-20组合差产生的9个差值小计，按小计值从上往下为{-1,-3,-6,-10,-15，-21,-28,-36,0}，合计值“-120”。

如果各自的小计值，以上数减下数进行统计，正数的2个小计差值的合计数均为“-8”，取差值正数{7,6,5,4,3,2,1}，合计28数。如果取正负绝对值，合计值为64(28+36=64)，2个正数单元的正负绝对数合计值为“128”（64+64=128）。而负数的2个小计差值的合计数为“-1”，如果取差值正数{2,3,4,5,6,7,8}，合计值35,如取正负绝对值，合计数分别为71（35+36=71），2个负数单元的正负绝对数合计值为“142”（71+71=142）。

以上纵向差值，共产生4个小类（{148,120,-121,-120},合计“27”）；如果按小计差值的合计数统计，{-8,-8,-1,-1},合计“-18”。取正数的结果，4个小类分2类，正数合计值为{28,35}，总计126（28×2+35×2=126）；按负数统计，均为“-36”数，总计-144（-36×4=-144），小计差值的正负数合计“-18”（126-144=-18）。如取正负绝对值，合计为270（126+144=270）。按1-9数平均统计，270/9=30。

此外，纵向4个小类，按出现值的个数统计，前11个（第1-11）三角形组合产生的90个差值中，正数43数，负数37数；后10个(第11-20)三角形组合产生的81个差数中，正负个数各自为36数，外加零值分别有{10,9}，故前11个三角形组合差共90个数值（43+37+10=90），后10数个三角形组合差中共81个数值（36+36+9=81）。正负个数差为6（43-37=6）。

由此，根据以上的纵横差值综合考虑，可以得到以下3个结论。

（1）8个小类按单元小计个数分类，横向为{9,9,9,9}，合计36个小计值；纵向为{10,10,9,9}合计38个小计值，纵横小计值个数差2数（38-36=2）。横向去除3个“0”值小计，实际个数为{8,9,8,8}，合计33个小计值，纵向如去除4个“0”值小计，实际个数为{9,9,8,8},合计34数，纵横差1数（34-33=1）。故纵横按正负数的个数分类，共74个小计值，其中有7个小计值为“0”（零）值。去除“0”（零）值，剩余67数的纵横差1个小计数。

（2）8个小类按单元合计数分类，共5个数值（即{-121,-120，112,120,148}），正负各自{120}出现2次，共4次；{-121}出现2次；{112,148}各一次，8数合计值为18（-9+27=18）。

按出现的正负值分类，正数{112,120,120,148}合计500；负数{-121,-121,-120,-120}合计“-482”，正负值合计为“18”（500-482=18）。取绝对值{500,482}的数之和1值为{5,14}，合计19(5+14=19)；数之和终值均为“5”，合计“10”(5+5=10)。500为第56个“5”数（500=5+55×9），482为第54个“5”数（482=5+53×9），56+54=110，500+482=982，故982为第110个“1”数（982=1+109×9）。

从数之和值角度观察，单元数取绝对值，120数的数之和终值为“3”，{112,121,148}的数之和1值为分别为{4,4,13}，数之和终值为均为{4}。按出现的正负数统计，正数{112,120,120,148}的数之和1值为分别为{4,3,3,13}，合计“23”，数之和终值为{4,3,3,4}，合计“14”；负数{121,121,120,120}的数之和1值与数之和终值相同，各为{4,3,3,3}，合计“14”。纵横数之和终值合计为“28”（14+14=28），这结果也应该与28星宿有关。

（3）8个小类按小计差值的正负数分类，横向差值取正负数的合计值为“0”（零）值，

4个小类正数合计值为“63”数（12+12+19+20=63）。纵向差值，取正数的合计值126{（28+35）×2=63×2=126}，取负数的合计值均为“-36”数，合计144（36×4=144），正负差为18（144-126=18）。故按正数统计，纵向正数值为横向的2倍（126/63=2），正数纵横差为63数；按负数统计，纵横差为81数（144-63=81），8个小类纵横正负差合计18（81-63=18）。

以上计算表明，陶缽的第2与第3三角形的上部间隔18毫米，是计算出来的结果。但具体有什么意义，这里尚不可知。同时作为计算结果，{33,34}、{23,14,28},{18,36,63,81,144}将在之后的章节中，得到运用。

 3 陶缽的其他信息

考古资料中明确第1、2、4～10九个三角形的面积等大，宽端为5厘米，九个三角形及第三、四两个三角形之间的间距相等，均为1.5厘米，而第2与第3两个三角形的间距，区别于其他三角形的间距，上为1.8厘米、下为1.2厘米，第3个三角形是正置的，底边宽3.8厘米。如果把概念扩大，按照毫米计量，{12,15,18}三个数字是否有特别意义，因为三者合计45数（12+15+18=45）与第3个三角形的锥刺合计数吻合。{38,50}与{12,15,18}之间的关系是什么？表1-14是对{12,15,18,38,50}的5个数字进行了计算，并且通过对表1-1、表1-2的分析，1～19个三角形的数之和值，除第3个三角形以外，其他所有的三角形数之和值按顺序排列，且11～19个三角形组合数的个位数等于数之和的数字，第20个三角形的数字开始就不再对应，之后再次对应，要到101～109个三角形的合计数的个位数时，末位数才与数之和的数字匹配，所以在1～100的三角形组合中，“19”这数字很重要。如果不考虑数之和的概念，把第2个三角形的顶端锥数10加上第3个三角形的底部9的数字，合计同样是“19”数。19这数字还有一个特点，连续做加法，1+2+3+…+17+18+19=190，190÷5=38，19×2=38。第二、三两个三角形的底边长{50,38}的合计数为88（50+38=88），与表1-5中取100数进行合计，除“1”数出现的12次以外，其余8数出现的频次是88（8×11=11）次，分连续5次与连续6次出现，可以吻合。同时，按照其他9个三角形底部10个锥数边长50毫米推算，平均每个锥点为5毫米（50/10=5），第3个三角形底部9个锥点，按5毫米的比例长度应该是45毫米，但第3三角形的长度实际为38毫米，45-38=7，比平均数少7个毫米。

在考古资料中写到“现存的三角形纹带已部分残损，但还剩下十个三角形”，可以理解为，三角形锥体部分虽有损坏，但是纹带由有十个三角形组成是明确的，所以，三角形锥体正置和倒置各5个，如果把正置作为底部，倒置称为顶部，根据表1-15计算底部合计为385毫米，顶部合计为403毫米，顶部和底部的周长差为18。把考古资料的数据全部利用上的话，如果顶部周长减少第3个三角形的底边38，可得365数（403-38=365），同理，底部周长减少365数，可以得到20数（385-365=20）。假设已经具有太阳一周年天数365数的概念，可得到{20,38}（385-365=20，403-365=38）二个数值。20是底部其他4个三角形总长的1/10倍（50×4÷10=20）。根据上述表1-2的计算结果，20又是一个变化数，在总数100个三角形的范围内，第20个开始三角形显示的自然数的个位数值与数之和的数值不再相等。

              表1-14  第2、第3三角形数据的关系         

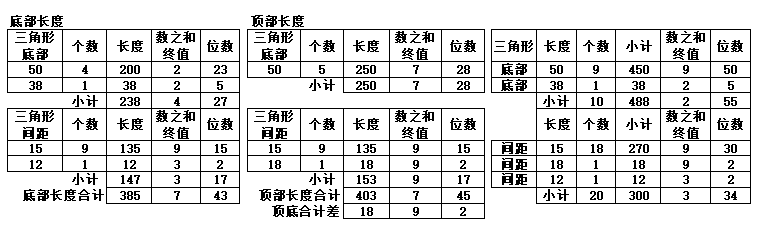
 表1-15  10个三角形顶底部的长度计算    （单位：毫米，个）

按表1-15中的10个三角形总长度488和10个三角形的20个间隔距离300考虑，488的数之和1值为“20”，终值为“2”，是第55个“2”数（488=2+54×9；54+1=55）；300的数之和终值为“3”，是第34个“3”数（300=3+33×9；33+1=34）。顶底合计长度788（488+300=788）的数之和1值为23(7+8+8=23),终值为“5”，是第88个“5”数（788=5+87×9；87+1=88）。

如果潮汐专家告诉我们，月球与太阳对地球的引潮力之比为11:5，它们的最小公倍数为55，除去第3个三角形以外的每个三角形数的合计为55，55可以代表月球与太阳的引潮力的公倍数，而且第3个三角形的底部38与第2三角形间距12。第3个三角形与其他三角形的底边差为12（50-38=12），同时底部总间距为147（15×9+12=147）的数之和1值为12（1+4+7=12），终值为“3”，12/3=4。如果按1年4季12个月计算，这些数据均与陶缻的第2、第3三角形有关联性的话，所以该文物的价值不只是数学范围上概念，应该可以扩大至天文学范畴，365是一年的天数，底部4个10锥数的三角形，间距如按12计算，一年可以分为4季12月。

4 陶缽的天文学意义

如今我们把人类居住的星球冠名为地球，作为天文的基本知识，认为地球是太阳系中一员，太阳系又是银河系的一个组成部分，但当时（距今6000年以上）的古人可能不是那么考虑，通过观天象，认为太阴（月亮）、太阳对地球影响很大，太阴（月亮）平均每15天变化一次，月圆月缺平均15天一次，所以1个月按30天计算就有2次变化，因月亮绕地球运动的同时，地球也绕太阳运动，30日并不是月亮绕地球的实际天数，故把月亮绕地球转动过程中途径的28组恒星星座，作为月亮运行位置的记录，每组恒星各有名称，通称28宿(宫)。单纯计算月亮绕地球旋转一周的时间，叫“恒星月”需要27.32166天（即27天7小时43分11秒）；从月朔(当月初一)到月朔(下月初一)，或从月望(满月)到月望(下一次满月)，被称为“朔望月”，平均日数为29.53059天（即29天12小时44分3秒）。

月亮绕地球一周称为“月份”，地球绕太阳一周称为“年份”，月亮运行有“恒星月”和“朔望月”之分，那地球绕太阳也有“恒星年”和“回归年”之分，以某一遥远恒星为参照物，地球公转的角度为360度，在地球绕太阳的同时2次经过参照物的时间为“恒星年”，长度是365.2564日（即365日6时9分10秒），而“回归年”按照太阳光直射到地球赤道算春分开始，从赤道北移到北回归线叫夏至，重新回到赤道为秋分，太阳光直射到南回归线称冬至，太阳直射光再次回到赤道，开始新的一年，所以回归年的长度是365.2422（365日5时48分46秒）。当时的古人应该有运转一圈360度的概念（即表1-14的360公倍数概念），但不确定是否有“恒星年”的定义，所以按照“朔望月”、“回归年”的概念，以29.53059天（实际按大月30天，小月29天），1年12个月365.2422日算历法就有必要进行调整。

求回归年日数与朔望月日数的最小公倍数，假设Y个回归年的天数与M个朔望月的天数相等，也就是等式：

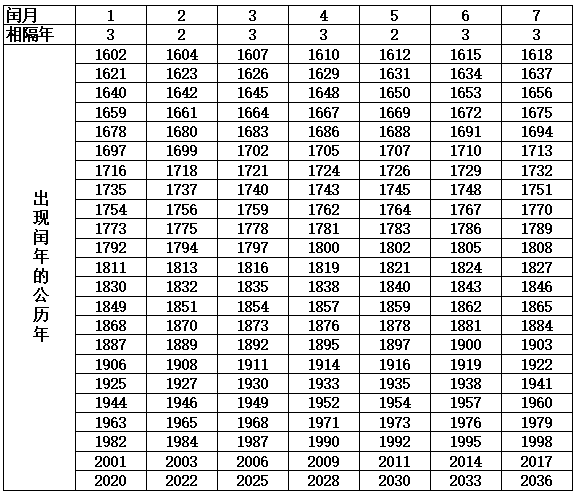
计算结果19个回归年与235个朔望月的日数仅有0.08685日之差（合2小时5分3秒）。看起来是相当精密的。这样十九年七闰的概念就产生了，在19年中增加7个闰月，通过闰月的设置，调整了“朔望月”与“回归年”之间的矛盾，是兼顾月亮绕地球的运动周期和地球绕太阳的运动周期而制定的历法。历月的平均长度接近朔望月，历年的平均长度接近回归年，是一种“阴月阳年”式的历法。它既能使每个年份基本符合季节变化，又使每一月份的日期与月相对应，所以中国的历法是阴阳合历。如果再仔细分析表1-14数据，可以看到360是｛1,2,3,4,5,6,8,9｝的公倍数，且其他数字以及比例关系中，唯独没有与7有关的数字，所以，推测要把1～9的数字都表示完整，还需要加7，这就是天文历法中的19年加7个闰月的概念，也是第3三角形设定为38数的理念。从西汉（西元前206年—西元8年）的《太初历》（西元前104年开始执行）之后，19年中增加闰月的年份是{3,2,3,3,2,3,3}，且出现的末位数在表1-16中，从上往下是有规律的排列的。

换言之，陶缻第3个三角形底边的边长设38数，可以认为是1+2+3+4+5+6+8+9=38的结果，1～9的合计为45，45-7=38。而表1-15的10个三角形顶、底部的长度{403,385}的数之和1值为{7,16},合计23数，数之和终值均为“7”数（4+0+3=7；3+8+5=16，1+6=7），合计14（7+7=14）。这说明，如果用数之和1值理解元君庙陶缻，上下长度差“9”数（16-7=9）；按照数之和终值计算，上下差为“0”（零），上下合为“5”数（7+7=14；1+4=5）。且上下数之和终值相等，用2个数之和终值“7”数表述，是非常强调“7”数的重要性，这与元君庙墓地中有7个空墓可能有关联性。

            表1-16  十九年七闰表（按无中气置闰原则排列）

                                   注：无中气置闰根据西汉的《太初历》制定的闰月方法。

如果根据第3三角形底部为9数，共45个锥数计算，第1至第3，3个三角形叠加总锥数为155（110+45=155），以此类推，10个三角形的叠加总锥数为540，而根据表1-1，10个三角形的锥数合计{55,110,155,210,265,320,375,430,485,540}为2945，5等分得589（2945÷5=589），540与589的差值为49（589-540=49），7×7=49，同样强调7数的重要性。

此外，385数是1～10的平方数的合计数；以及8～11的平方数加19的合计数。而403是7～11的平方数减12的合计数。

385 =1×1+2×2+3×3+4×4+5×5+6×6+7×7+8×8+9×9+10×10

=1+4+9+16+25+36+49+64+81+100

=8×8+9×9+10×10+11×11+19=64+81+100+121+19=366+19

403 =7×7+8×8+9×9+10×10+11×11-12=49+64+81+100+121-12=415-12

385=7+9×42=7+378 ； 403=7+9×44=7+396  

385的数之和终值为“7”，64+81+100+121+19=385，{64,81,100,121,19}的数之和终值各自为{1,9,1,4,1},合计16，数之和终值也为“7”。而403 =415-12，{415,12}的数之和1

值为{10,3}，10-3=7。如按数之和终值为{1,3}计算，1-3=-2，如果当时已经具备“2”与“7”合计为9的概念，在数之和理论中“-2”与“7”互为表里，“-2”数与“7”数概念一致。说明如用正数“7”表示，其背后的真实意义可能有“-2”数的存在。因此，数之和值做加法没有问题，但如做减法，会出现负数，还需要再添加一个“9”数，最后改用正数表示。

按数之和值的概念理解“7”数，{7,16,25,34,43,52,61,70,……}，是以“7”开始的9数等差数列。385为第43个“7”（385=7+42×9），403为第45个“7”（403=7+44×9）。

上下合计88个“7”，且385数是7数的55倍（385÷7=55），陶缽底部总长度设定为385数的用意在天文历法上，是否还有其他寓意？

关于原始社会，至今并没有发现相应的文字资料，故不能用文献进行阐述，但如果根据后世的文献资料中，对应一部分天文历法上的具体内容，应该可以做一些说明。

东汉史学家班固（西元32年-西元92年）编撰的《汉书》，是继司马迁（西元前145年-西元前90年）《史记》之后，中国古代又一部重要史书，《汉书》第21卷下<律历志·统母>中有以下的内容记载：

日法八十一。元始黄钟初九自乘，一龠之数，得日法。

　　闰法十九，因为章岁。合天地终数，得闰法。

　　统法一千五百三十九。以闰法乘日法，得统法。

　　元法四千六百一十七。参统法，得元法。

　　会数四十七。参天九，两地十，得会数。

　　章月二百三十五。五位乘会数，得章月。

　　月法二千三百九十二。推大衍象，得月法。

通法五百九十八。四分月法，得通法。

周天五十六万二千一百二十。以章月乘月法，得周天。

《汉书》中的<律历志>，主要是对西汉（西元前202年-西元8年）的2部重要历法《太初历》与《三统历》的记录，《太初历》主要由当时的天文学家落下闳(西元前156年-西元前87年)、邓平、唐都等人编制，从汉武帝(西元前156年-西元前87年)的太初元年（西元前104年）起到汉哀帝(西元前26年-西元前1年)的绥和2年(西元前7年)止，共施行97年，但并没有保留下历法的术文。《三统历》于西汉哀帝绥和2年(西元前7年)开始实施，至东汉章帝元和2年(西元85年)被四分历取代，由西汉著名学者刘歆编纂，是中国史书上第一部记载完整的历法，为《汉书》历法部分的蓝本。而<律历志·统母>是当时天文历法中的最高准则。

在《汉书》的<律历志>上中，记载“闳运算转历。其法以律起历，曰：「律容一龠，积八十一寸，则一日之分也。与长相终。律长九寸，百七十一分而终复。三复而得甲子。夫律阴阳九六，爻象所从出也。故黄钟纪元气之谓律。律，法也，莫不取法焉。」与邓平所治同。于是皆观新星度、日月行，更以算推，如闳、平法。法，一月之日二十九日八十一分日之四十三”，大意是落下闳通过计算进行历法的运算，其方法是根据音律，以律龠（黄钟律管）的长度9寸之数，9×9=81，作为一日的长度，9×19=171作为重复对象，3×171=513，可复得甲子。律中的阴阳数字用九和六，是从爻象所演化而来的。根据黄钟来纪元，黄钟之气就叫律。律，也就是法则，没有不取律为法则的。落下闳研究结果与邓平相同。于是，大家重新观察星度以及日月的运行，并加以推算，与落下闳、邓平一致。定法则：一月有二十九天八十一分之四十三。

因此在统母中规定， “日法八十一。元始黄钟初九自乘”的概念是，1日按九数自乘，九九得八十一数为计算单位，九九八十一的概念是根据黄钟的音律律管长度9寸得出的结果，故“日法”为81数。“闰法十九，因为章岁。合天地终数，得闰法”的意思是，按19年闰7，1年12个月计算，可得章月235数（19×12+7=235）。235为1个章岁，天地阴阳合，为闰法。“统法一千五百三十九。以闰法乘日法，得统法”的意思是按日法81数乘以19年为1539数，称为统法（81×19=1539）。“元法四千六百一十七。参统法，得元法”，即参同叁，3个统法为4617（1539×3=4617）。

此外“会数四十七。参天九，两地十，得会数”。参（通“叁”）天九，两地十，即用3个天数（9数）和2个地数（10数）得会数47（3×9+2×10=47）。“章月二百三十五。五位乘会数，得章月”，即5个会数得235（47×5=235）为一个章月。“月法二千三百九十二。推大衍象，得月法”的意思是月法根据日法推算而来，81×29=2349，2392-2349=43，故2392÷81=29又43/81。“通法五百九十八。四分月法，得通法”即按月法2392进行4等分，得通法598（2392÷4=598）。“周天五十六万二千一百二十。以章月乘月法，得周天”，即235×2392=562120。                                 

以上是《汉书·律历志·统母》的规定，但为何如此规定，并没有具体的计算过程。如果把<统母>的概念按照元君庙陶缻的设计进行解释，是否可以得到以下的结论。

（1）第2三角形底部锥数10，第3三角形底数锥数9。

  根据阴阳合原则：正三角为阳，倒三角为阴；上阳下阴；奇数为阳，偶数为阴，阴阳合，故第2三角形的底部上阳对应阴数10，2×10 = 20；第3三角形底部下为阴，对应阳数9，3×9=27，第2与第3三角形的底部锥数分别根据乘数计算，合计47（20+27=47），得会数。

（2）10个三角形的总锥数共540数。

根据表1-15的计算结果，顶部与底部的周长403与385进行合计，合计值788与通法598的差值为190数（788-598=190），正好是1-19的连续加法值。如按10个三角形的总锥数共540数计算，与通法598差58（598-540=58）数，58数与陶缻的顶部、底部各自与365数得差值{38,20}的合计数一致，所以这样的结果应该是设计之初就已经安排好。

10个三角形叠加的合计数{55,110,155,210,265,320,375,430,485,540}，其数之和终值分别为{1,2,2,3,4,5,6,7,8,9}，这10个数值的合计为47数，即47数作为会数，可以用“参天九，两地十”法计算，也可以用陶缻的10个三角形的数之和值叠加计算。

  （3）5个会数得章月。

   陶缻上下各5三角形，按顶部三角形5数计算，47×5=235；根据底部第3三角形计算，（50/10）×9-38=45-38=7；235=12×19+7，故需要添加7个闰月，太阴历与太阳历可以调和。

   关于5数的概念有更重要的意义包含在其中。表1-17以及表1-18是对元君庙陶缻的10个三角形的锥数计算进行扩大，表1-17中可以看到，以10个三角形为一个组合，第1个组合数为47，从第2-9个组合数(第11-第100个三角形)的组合数为{46,47,48,49,50,51,52，53,54}，之后也以{46,47,48,49,50,51,52,53,54}进行循环。表1-18在表1-17的基础上，再度扩大三角形数字，并对表1-18中的10组合的小计数按数之和值进行计算，表中的开始数以及结束数为三角形的使用数值，发现按10数为一个组合，10个组合为一个单元，其单元组合值依然按{47,46,47,48,49,50,51,52,53,54}出现,以数之和值统计，合计值也是47，且需要100个组合，10个单元1000个三角形的数值才可以重新得到47数，即比较之前的10组合扩大了100倍的三角形数。按奇、偶数分类，{47,46,47,48,49,50,51,52,53,54}中有5个奇数（即{47,47,49,51,53}）和5个偶数（即{46,48,50,52,54}）。奇数合计247，偶数合计250，奇数与偶数差3数（250-247=3）。250的数之和终值为“7”数，247的数之和终值为“4”数，同样差3数。

   如按数之和值统计，{47,47,49,51,53}的数之和值为{2,2,4,6,8}，合计22；{46,48,50，52,54}的数之和值为{1,3,5,7,9}，合计25，2组数之和值的合计数为47（22+25=47），差值3数（25-22=3）。这样原先的奇数组合（{47,47,49,51,53}，合计247）的数之和值变为偶数组合（{2,2,4,6,8}，合计22）；原先的偶数组合（{46,48,50,52,54}，合计250）的数之和值变为奇数组合（{1,3,5,7,9}，合计25），按奇数为阳，偶数为阴的原则，同样也体现了可以遵循阴阳互换的原则，即阳中有阴，阴中有阳。

 （4）第1、2、3三角形底部锥数合计数29（10+10+9=29）；外加第3三角形的底部9数，九九八十一（9×9=81），81与第3三角形底边长38，差43（81-38=43），故得月法的2392数（81×29+43=2392）。

 （5）按第2三角形底部锥数10，第3三角形底数锥数9，上下底部锥数合计19，日法81，81×19=1539为统法，外加底部周长385，365×1539+385=561735+385=562120为周天。

 （6）最终结论

 按日法81数，月法29又81分之43数，年法365又1539分之385，47会数235个章月，19年计算：

太阴（月亮）235朔 ：

太阳19年 ：       

 周天562120代表着81分之562120数能使阴阳合。562120的数之和1值为16（5+6+2+1+2=16），终值数之和为7（1+6=7）。说明7数在数之和理论中有非常重要的作用。

      表1-17 三角形锥数的数之和值统计（1）

      表1-18 三角形锥数的数之和值统计（2） 

而《汉书·律历志》中的“黄钟纪元气之谓律”，实际是根据数之和理论（9进制）的计算结果，当然，数之和理论（9进制）也可能是根据音乐的和声发展而来的。无论数之和理论的产生从何而起，至少作为一种数学的计算方法，会数的概念提出，在元君庙仰韶墓地的陶缻中，就是运用数之和理论，10个三角形锥数的组合值，通过数之和值的转换，计算出的结论。会数的概念在天文历法中，有着非常重要的地位（因为可循环）。具体的内容在后续，还将做详细论述。

根据以上计算结果，可以明确地得出这样的结论：元君庙仰韶墓地的陶缻（M413:5），堪称天文历法上的极品。完全能证明，（按最保守的观点）在西元前4000年左右（距今应该有6000年以上），中华文明在数学、天文学乃至哲学层面，已经达到了相当高的高度。

                                                                                                                 （第1、2节完，第3节待续）