博文
黎曼面与语义拓扑
||
关于黎曼面的两种表达
对黎曼面是什么,至少存在如下两种描述:
1. 黎曼面是一维的复流形【1】。
2. 黎曼面是一小圈的弦在高维时空中移动时扫过的面【2】。
对于非数学专业人员,
见了描述1,除了能提取【黎曼面】【一维】【复流形】关键字外,头脑中可能一片空白。
见了描述2,不但能提取关键字【黎曼面】【弦圈】【高维时空】【扫移】【过面】,而且头脑中还能想象出下面的图像:
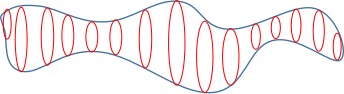
图1:黎曼面是一小圈的弦在高维时空中移动时扫过的面
这里引出了3个问题:
1. 为什么对同一个概念的上述两种语言文字组织的表达会产生不同的效果?
2. 为什么有了能获得更广泛理解的表达2,还需要只能获得更狭隘范围理解的表达1?
3. 如何能将第2种表达,平滑转换对应到第1种表达呢?
黎曼面是一种数学空间,也就是一种描述空间的数学方法。在回答这三个问题之前,可以回归到数学方法的出发点,探讨一下数学空间和物理空间的关系,为过渡到从语言含义的角度来探究这些问题的答案做个铺垫。
数学空间和物理空间的关系
把数学空间理解为就是对物理空间的想法和看法,对理解两类空间都是有利的。
广义的物理空间是可用数量来描述的物理上的客观实在。通常用x-y-z坐标系描述的视觉空间,只是众多用数学方法表达物理空间的例子中的一个。数学空间是人类对物理空间的认识工具。所以,不同类型的数学空间,可以理解为是对同一个客观存在的物理空间,选择用的不同的“看法”来看,对一个部分或整体,所得到的不同认知与推断的结果。人类认识世界的目的,就是想通过寻找【认知推断结果】和【真实物理空间表现】之间的、可复现的完整一致性,去发现物理空间本来的模样。
数学家是在“某种对空间的看法”基础上,通过附加或剔除不同的检测和约束的条件,来得到对物理空间进行认知的工具的。当然,很大部分数学家只专注于把玩纯粹的看法,自己是从不用这些看法来对照看物理空间的。其意义是:看法多了,总会为寻找那一款特别适合物理空间的看法提供更多的参考。
在“看法”方面,数学家可取不同的【维度个数】来看;可在【空间之外】看空间整体和局部,也可在【空间之上】一点一点移动摸索【空间的极小区域】及其与【相邻区域的关系】来看空间;可用不同的移动、旋转、投影、切片的方法作用在空间上,来观察、测量空间模样变与不变的规律;可在不同维度上取【相同或不同的缩放比率(尺度)】来看;可在维度上的【不同位置】上取【相同或不同的缩放比率】来看;可【捆绑或拆分】【多个维度联合的意义】来看,还可【捆绑或拆分】多个不同看法来看,等等。通过变换、拆分、组合看法,空间就会显现出在不同看法下的不同模样。
总之,如果将物理空间比喻是一只魔方,数学家就可比喻为玩魔方的玩家。
可以想象,如果某类看法恰好与空间自身的结构是吻合的,那么,这类看法就既能反映空间的全貌,又能得到最简单的空间模样。其他的看法,要么得到简单模样,但会损失空间的信息;要么会割裂和重叠空间的信息,使看到的空间模样变得比实际更复杂。
黎曼面的看法
一个实数变量可代表一条数轴,是一个一维的实空间。这是用来将物理空间中的位置关系用【平直移动】的看法来看待的数学工具。黎曼面只是类似的另一个不同的看法而已。
说黎曼面是一维的复流形,得先理解什么是流形。从语义对应来看,流形就是一种数学空间,对物理空间的一种看法。是什么样的看法呢?就是上节提到的:
“在【空间之上】一点一点移动摸索【空间的极小区域】及其与【相邻区域的关系】来看空间”
的看法,并且对空间极小区域的看法,是在极小区域内部采用平直移动看法,但移动到相邻区域上时,就不一定是平直移动了,而是需要平滑的移动的看法。
也就是说,用这种看法来看空间,就把空间看成是流形了。
既然是黎曼面是复流形,那么,黎曼面就是用复数来描述的空间。
一个实数变量代表一个数轴,是一个一维的实空间。
一个复数变量,捆绑了两个实变量:z=a+bi,这和直接捆绑2个实变量(a,b)的区别是:对【复变量的捆绑】赋予了特别的整体上的意义,即:一个复变量是从虚和实两个侧面共同、同时描述的整体。这两个侧面是各有含义,相互是不能互换、对接的。也就是说,复数捆绑的实部和虚部的两个实数是不可拆分的整体,即:即使其中之一虚部取0,也是虚部取0的一个复数,而不是一个拆分出来的实部单独的实数。直接捆绑2个实变量(a,b)的a,b是两个对等含义的实变量,可拆分、可互换含义、可对接。这种差异,会给它们所表示的空间,带来变换、转换和对接上的不同约束,从而使其可表示的空间具有不同的模样。
所以,黎曼面是一个捆绑在一起的2个实维度,并赋予了相互不可分割、互换、对接的整体含义的2维实空间。如果同样采用“流形”的看法,和直接捆绑2维实空间的(a,b)流形的不同是:
用(a,b)表示的点,因a,b是对等独立的实数,所以a,b数值的变化,分别表示空间位置上沿a或b方向分别进行的平直移动。按流形的看法,a,b数值的连续微小的变化,是在二维空间上做连续微小的相互垂直的移动扫过的阶梯状轨迹,严格来说,这不能认为是在二维平面上的“光滑”移动。唯一可认为是光滑的移动的方式,就只能是先连续变化一个变量扫出一根直线,再用这根直线连续向垂直方向移动扫出整个平面。
a+bi表示的点,a,b是捆绑在一起的整体,a,b数值的变化量虽然可以不同,但必须看成是同时的变化,其所表示的点的移动,只能沿有倾斜角的直线的移动。按流形的看法,就只能直接产生一个二维实空间,连续的具有不同倾斜角的微小的直线移动,就可以产生光滑的曲线位置的移动来扫过二维的平面空间。
语义拓扑
任何一段语言文字的表达,都是通过连接一串关键字词汇来实现的。而每个关键字词汇在表达中都具有特定的词义,所以一段语言文字的表达,首先是一串一串的词义顺序连接,也就是一句一句的话编织而成的一个词义的网络。
而一段文字所要表达的目标含义,并不是上述的词义网络,而是存在于描述者思想意识中的特定的知识内容。这些知识内容包含若干概念,以及这些概念之间的连接关系。如果把每个独立的概念理解为是一个唯一的语义,那么,概念关系的网络,就构成了一个语义拓扑结构,简称语义拓扑。
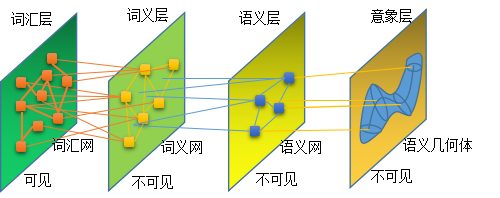
假设可以将语义拓扑理解为是一个虚拟的几何体的拓扑结构,可称这个虚拟的几何体为“语义几何体”,那么,被表达的对象可以“物化”为这个语义几何体,语义拓扑只是这个语义几何体的“中心思想”。
而词义网络,可以理解为是从某个侧面对语义几何体的语言符号化的表达,即语义几何体在某个投影面(表达面)上离散化的投影。词义网络就是以词义为点,词义关系为边的,描述语义几何体的一个三角剖分网格。
语义几何体假设可能成立的证据是:通常对一个思维意识产物的表达,确实是需要从多个不同的侧面进行表达和理解,才能获得对该思维意识产物更完整、准确的,在意识主体之间的迁移,即实现所谓的沟通。这已经是现代沟通理论的常识。这与几何体可以不同方向上得到多个三角剖分网格模型视图的事实对应得体。类似对应得体的事实最少还有:
1. 一个几何体只会有一个几何拓扑结构;对应:一个意识产物只有一套中心思想;
2. 对一个几何体可建立不同的三角剖分网格模型,对应:对同一个意识产物,仅出于文章的行文构思的不同(词义网络选择不同),就可写很多篇不同的文章;
3. 对一个几何体的同一个三角剖分网格模型,选择不同的纹理贴图,还可得到多个不同视觉效果的版本,对应:对同一套行文构思(相同的词义网络),还可以用不同的词汇符号来表达得到不同的表达版本(如对同一本书的不同语种的翻译版本)。
注:此处黎曼面概念指采用平直度量的连续空间,二维来看,就是任意形状的连续光滑的封闭的表面。
数学上的黎曼面还有另外一个概念,用来对复变函数单值化的解析曲面,二者是完全不同的概念且联系疏远。
https://blog.sciencenet.cn/blog-33982-1290073.html
上一篇:智能认知随想
下一篇:突破终极限制的数——极数