博文
概念辨析:自旋极化、自旋轨道耦合、磁性及电子之间的库伦排斥
||
关注:
1)上述参数的物理意义及内涵
spin-polarized local density approximation (LDA)
2) 计算过程中的参数设置,如 ISPIN=2,Hubbard parameter U (描述处于相同原子轨道的电子之间的库伦排斥)
来自wikipeida
http://en.wikipedia.org/wiki/Spin_polarization
Spin polarization is the degree to which the spin, i.e., the intrinsic angular momentum of elementary particles, is aligned with a given direction.[1] This property may pertain to the spin, hence to the magnetic moment, of conduction electrons in ferromagneticmetals, such as iron, giving rise to spin-polarized currents. It may refer to (static) spin waves, preferential correlation of spin orientation with ordered lattices (semiconductors or insulators).
It may also pertain to beams of particles, produced for particular aims, such as polarized neutron scattering or muon spin spectroscopy. Spin polarization of electrons or of nuclei, often called simply magnetization, is also produced by the application of a magnetic field. Curie law is used to produce an induction signal in Electron spin resonance (ESR or EPR) and in Nuclear magnetic resonance (NMR).
Spin polarization is also important for spintronics, a branch of electronics. Magnetic semiconductors are being researched as possible spintronic materials.
The spin of free electrons is measured either by a LEED image from a clean wolfram-crystal (SPLEED)[2][3][4] or by an electron microscope composed purely of electrostatic lenses and a gold foil as a sample. Back scattered electrons are decelerated by annular optics and focused onto a ring shaped electron multiplier at about 15°. The position on the ring is recorded. This whole device is called a Mott-detector. Depending on their spin the electrons have the chance to hit the ring at different positions. 1% of the electrons are scattered in the foil. Of these 1% are collected by the detector and then about 30% of the electrons hit the detector at the wrong position. Both devices work due to spin orbit coupling.
The circular polarization of electromagnetic fields is due to spin polarization of their constituent photons.
In the most generic context, spin polarization is any alignment of the components of a non-scalar (vectorial, tensorial, spinor) field with its arguments, i.e., with the nonrelativistic three spatial or relativistic four spatiotemporal regions over which it is defined. In this sense, it also includes gravitational waves and any field theory that couples its constituents with the differential operators of vector analysis.
References[edit]
Jump up ^J. Kessler (1976). Polarized Electrons. Springer Verlag Berlin Heidelberg. pp. 7–19. ISBN 0-387-07678-6.
Jump up ^J. Kirschner and R. Feder (1979). "Spin Polarization in Double Diffraction of Low-Energy Electrons from W(001): Experiment and Theory". Physical Review Letters42 (15): 1008–1011. Bibcode:1979PhRvL..42.1008K. doi:10.1103/PhysRevLett.42.1008.
Jump up ^M. Kalisvaart, M. R. O'Neill, T. W. Riddle, F. B. Dunning, and G. K. Walters (1977). "Electron-spin polarization in low-energy electron diffraction from tungsten (001)". Physical Review B17 (4): 1570–1578. Bibcode:1978PhRvB..17.1570K. doi:10.1103/PhysRevB.17.1570.
Jump up ^R. Feder (1976). "Spin Polarization in Low-Energy Electron Diffraction from W(001)". Physical Review Letters36 (11): 598–600. Bibcode:1976PhRvL..36..598F. doi:10.1103/PhysRevLett.36.598.
自旋极化(英语:Spin polarization)可以用来度量基本粒子自旋的角动量和一个给定方向吻合的程度[1]。这个属性可能属于自旋,从而也属于金属传导带(例如铁)的磁矩,它们促进了自旋极化电流(spin polarized currents)。它也可以指(静态的)自旋波
LDA & LSDA
Local-density approximations (LDA) are a class of approximations to the exchange-correlation (XC) energy functional in density functional theory (DFT) that depend solely upon the value of the electronic density at each point in space (and not, for example, derivatives of the density or the Kohn-Sham orbitals). Many approaches can yield local approximations to the XC energy. However, overwhelmingly successful local approximations are those that have been derived from the homogeneous electron gas (HEG) model. In this regard, LDA is generally synonymous with functionals based on the HEG approximation, which are then applied to realistic systems (molecules and solids).
In general, for a spin-unpolarized system, a local-density approximation for the exchange-correlation energy is written as
![E_{xc}^{.mathrm{LDA}}[.rho] = .int .rho(.mathbf{r}).epsilon_{xc}(.rho). .mathrm{d}.mathbf{r}. ,](http://upload.wikimedia.org/math/8/8/6/8863f1340cd344249e12a99d5db362db.png)
where ρ is the electronic density and εxc, the exchange-correlation energy density, is a function of the density alone. The exchange-correlation energy is decomposed into exchange and correlation terms linearly,

so that separate expressions for Ex and Ec are sought. The exchange term takes on a simple analytic form for the HEG. Only limiting expressions for the correlation density are known exactly, leading to numerous different approximations for εc.
Local-density approximations are important in the construction of more sophisticated approximations to the exchange-correlation energy, such as generalized gradient approximations or hybrid functionals, as a desirable property of any approximate exchange-correlation functional is that it reproduce the exact results of the HEG for non-varying densities. As such, LDA's are often an explicit component of such functionals.
Homogeneous electron gas[edit]
Approximation for εxc depending only upon the density can be developed in numerous ways. The most successful approach is based on the homogeneous electron gas. This is constructed by placing N interacting electrons in to a volume, V, with a positive background charge keeping the system neutral. N and V are then taken to infinity in the manner that keeps the density (ρ = N / V) finite. This is a useful approximation as the total energy consists of contributions only from the kinetic energy and exchange-correlation energy, and that the wavefunction is expressible in terms of planewaves. In particular, for a constant density ρ, the exchange energy density is proportional to ρ⅓.
Exchange functional[edit]The exchange-energy density of a HEG is known analytically. The LDA for exchange employs this expression under the approximation that the exchange-energy in a system where the density in not homogeneous, is obtained by applying the HEG results pointwise, yielding the expression[1][2]
![E_{x}^{.mathrm{LDA}}[.rho] = - .frac{3}{4}.left( .frac{3}{.pi} .right)^{1/3}.int.rho(.mathbf{r})^{4/3}. .mathrm{d}.mathbf{r}. .](http://upload.wikimedia.org/math/6/9/4/6948547059dd91c24506cd0153b898d0.png) Correlation functional[edit]
Correlation functional[edit]Analytic expressions for the correlation energy of the HEG are not known except in the high- and low-density limits corresponding to infinitely-weak and infinitely-strong correlation. For a HEG with density ρ, the high-density limit of the correlation energy density is[1]

and the low limit

where the Wigner-Seitz radius is related to the density as

Accurate quantum Monte Carlo simulations for the energy of the HEG have been performed for several intermediate values of the density, in turn providing accurate values of the correlation energy density.[3] The most popular LDA's to the correlation energy density interpolate these accurate values obtained from simulation while reproducing the exactly known limiting behavior. Various approaches, using different analytic forms for εc, have generated several LDA's for the correlation functional, including
Vosko-Wilk-Nusair (VWN) [4]
Perdew-Zunger (PZ81) [5]
Cole-Perdew (CP) [6]
Perdew-Wang (PW92) [7]
Predating these, and even the formal foundations of DFT itself, is the Wigner correlation functional obtained perturbatively from the HEG model.[8]
Spin polarization[edit]The extension of density functionals to spin-polarized systems is straightforward for exchange, where the exact spin-scaling is known, but for correlation further approximations must be employed.
A spin polarized system in DFT employs two spin-densities, ρα and ρβ with ρ = ρα + ρβ, and the form of the local-spin-density approximation (LSDA) is
![E_{xc}^{.mathrm{LSDA}}[.rho_{.alpha},.rho_{.beta}] = .int.mathrm{d}.mathbf{r}. .rho(.mathbf{r}).epsilon_{xc}(.rho_{.alpha},.rho_{.beta}). .](http://upload.wikimedia.org/math/f/0/5/f056f6524aa8e8eaeacef2f28da80f6f.png)
For the exchange energy, the exact result (not just for local density approximations) is known in terms of the spin-unpolarized functional:[9]
![E_{x}[.rho_{.alpha},.rho_{.beta}] = .frac{1}{2}.bigg( E_{x}[2.rho_{.alpha}] + E_{x}[2.rho_{.beta}] .bigg). .](http://upload.wikimedia.org/math/b/d/3/bd3a47ecc38961e02a7fcae57bb6b77d.png)
The spin-dependence of the correlation energy density is approached by introducing the relative spin-polarization:

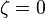 corresponds to the paramagnetic spin-unpolarized situation with equal
corresponds to the paramagnetic spin-unpolarized situation with equal 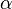 and
and  spin densities whereas
spin densities whereas 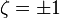 corresponds to the ferromagnetic situation where one spin density vanishes. The spin correlation energy density for a given values of the total density and relative polarization, εc(ρ,ς), is constructed so to interpolate the extreme values. Several forms have been developed in conjunction with LDA correlation functionals.[4][10]
corresponds to the ferromagnetic situation where one spin density vanishes. The spin correlation energy density for a given values of the total density and relative polarization, εc(ρ,ς), is constructed so to interpolate the extreme values. Several forms have been developed in conjunction with LDA correlation functionals.[4][10]
The exchange-correlation potential corresponding to the exchange-correlation energy for a local density approximation is given by[1]

In finite systems, the LDA potential decays asymptotically with an exponential form. This is in error; the true exchange-correlation potential decays much slower in a Coulombic manner. The artificially rapid decay manifests itself in the number of Kohn-Sham orbitals the potential can bind (that is, how many orbitals have energy less than zero). The LDA potential can not support a Rydberg series and those states it does bind are too high in energy. This results in the HOMO energy being too high in energy, so that any predictions for the ionization potential based on Koopman's theorem are poor. Further, the LDA provides a poor description of electron-rich species such as anions where it is often unable to bind an additional electron, erroneously predicating species to be unstable.[11][5]
References[edit]^ Jump up to: abcParr, Robert G; Yang, Weitao (1994). Density-Functional Theory of Atoms and Molecules. Oxford: Oxford University Press. ISBN 978-0-19-509276-9.
Jump up ^Dirac, P. A. M. (1930). "Note on exchange phenomena in the Thomas-Fermi atom". Proc. Cambridge Phil. Roy. Soc.26 (3): 376–385. Bibcode:1930PCPS...26..376D. doi:10.1017/S0305004100016108.
Jump up ^D. M. Ceperley and B. J. Alder (1980). "Ground State of the Electron Gas by a Stochastic Method". Phys. Rev. Lett.45 (7): 566–569. Bibcode:1980PhRvL..45..566C. doi:10.1103/PhysRevLett.45.566.
^ Jump up to: abS. H. Vosko, L. Wilk and M. Nusair (1980). "Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis". Can. J. Phys.58 (8): 1200. Bibcode:1980CaJPh..58.1200V. doi:10.1139/p80-159.
^ Jump up to: abJ. P. Perdew and A. Zunger (1981). "Self-interaction correction to density-functional approximations for many-electron systems". Phys. Rev. B23 (10): 5048. Bibcode:1981PhRvB..23.5048P. doi:10.1103/PhysRevB.23.5048.
Jump up ^L. A. Cole and J. P. Perdew (1982). "Calculated electron affinities of the elements". Phys. Rev. A25 (3): 1265. Bibcode:1982PhRvA..25.1265C. doi:10.1103/PhysRevA.25.1265.
Jump up ^John P. Perdew and Yue Wang (1992). "Accurate and simple analytic representation of the electron-gas correlation energy". Phys. Rev. B45 (23): 13244–13249. Bibcode:1992PhRvB..4513244P. doi:10.1103/PhysRevB.45.13244.
Jump up ^E. Wigner (1934). "On the Interaction of Electrons in Metals" (abstract). Phys. Rev.46 (11): 1002–1011. Bibcode:1934PhRv...46.1002W. doi:10.1103/PhysRev.46.1002.
Jump up ^Oliver, G. L.; Perdew, J. P. (1979). "Spin-density gradient expansion for the kinetic energy". Phys. Rev. A20 (2): 397–403. Bibcode:1979PhRvA..20..397O. doi:10.1103/PhysRevA.20.397.
Jump up ^von Barth, U.; Hedin, L. (1972). "A local exchange-correlation potential for the spin polarized case". J. Phys. C: Solid State Phys.5 (13): 1629–1642. Bibcode:1972JPhC....5.1629V. doi:10.1088/0022-3719/5/13/012.
Jump up ^Fiolhais, Carlos; Nogueira, Fernando; Marques Miguel (2003). A Primer in Density Functional Theory. Springer. p. 60. ISBN 978-3-540-03083-6.
局域密度近似(local-density approximation, LDA)是密度泛函理论的其中一类交换相关能量泛函中使用的近似。该近似认为交换相关能量泛函仅仅与电子密度在空间各点的取值有关(而与其梯度、拉普拉斯等无关)。尽管有多种方法都能体现局域密度近似,但在实际中最成功的是基于均匀电子气模型的泛函。下面的讨论,除非特别说明,仅限于这一类泛函。
一般地,对于非自旋极化的体系,局域密度近似的交换相关泛函可以写作:
![E_{xc}^{.mathrm{LDA}}[.rho] = .int .rho(.mathbf{r}).varepsilon_{.rm xc}(.rho). .mathrm{d}.mathbf{r}. ,](http://upload.wikimedia.org/math/f/7/d/f7d749dd78380c0b353034aed834b3dd.png)
 为电子密度,
为电子密度, 为交换相关能量密度,它仅仅是电子密度的函数。交换相关能可以分解为交换项与相关项:
为交换相关能量密度,它仅仅是电子密度的函数。交换相关能可以分解为交换项与相关项:

于是问题就变为分别寻找交换项和相关项的表达式。对于均匀电子气模型来说,交换项有着简单的解析式,而相关项只在特殊情况下有着精确的表达式。对相关作用的不同近似能够得到不同的  。对于实际应用的泛函来说,相关作用能量密度项的形式总是很复杂的。
。对于实际应用的泛函来说,相关作用能量密度项的形式总是很复杂的。
在构建泛函的过程中,局域密度近似有着重要的地位。基于局域密度近似的泛函是其它更复杂的泛函(如基于广义梯度近似(GGA)的泛函和杂化泛函)的基础。一般来说,人们要求所有的泛函都能正确处理均匀电子气模型,因此所有的泛函中都或多或少地包含局域密度近似项。
均匀电子气模型[编辑]
有多种方法构筑仅仅依赖于电子密度的交换相关能量泛函,其中最成功的模型是自由电子气模型。将  个有相互作用的电子放入体积为
个有相互作用的电子放入体积为 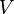 的空间内,并加入正电荷背景使体系处处处于电中性。然后让
的空间内,并加入正电荷背景使体系处处处于电中性。然后让  和
和 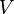 同时趋向无穷,同时保持电子密度
同时趋向无穷,同时保持电子密度  有限。此时的波函数可以用平面波表示。对于密度为常数的情形,交换能量密度与密度的平方根成正比。
有限。此时的波函数可以用平面波表示。对于密度为常数的情形,交换能量密度与密度的平方根成正比。
均匀电子气模型的交换能量密度有着精确的解析解。局域密度近似把这一解析的表达式推广到了电子密度不为常数的情形。把这表达式应用于空间的每一点上,并且在对全空间积分得到下式: [1][2]
![E_{x}^{.mathrm{LDA}}[.rho] = - .frac{3}{4}.left( .frac{3}{.pi} .right)^{1/3}.int.rho(.mathbf{r})^{4/3}. .mathrm{d}.mathbf{r}. .](http://upload.wikimedia.org/math/2/3/6/2363020ad450965a7fff8faff46569a5.png)
可以看出,这种推广只在空间处处电子密度都变化不太大的时候是有效的。请求解释
相关能量密度[编辑]均匀电子气模型的相关能量密度的解析表达式是未知的,但在高密度极限与低密度极限下(分别对应弱相关与强相关)的表达式是已知的。高密度极限下的表达式为:[1]

低密度极限下则为:

式中,维格纳-赛兹半径  与电子密度的关系为:
与电子密度的关系为:

对均匀电子气模型进行的精确量子蒙特卡罗模拟得到了中等密度下的相关能量密度。[3] 常见的局域密度近似相关泛函是通过对这些密度值进行内插法得到的,同时需要保证在高、低密度极限下正确的行为。下面列出了一些在密度泛函计算中使用到的交换能量密度泛函的符号与其作者。
Vosko-Wilk-Nusair (VWN) [4]
Perdew-Zunger (PZ81) [5]
Cole-Perdew (CP) [6]
Perdew-Wang (PW92) [7]
在上面这些泛函提出之前,甚至在密度泛函理论提出之前,人们广泛使用的是对均匀电子气模型进行微扰计算得到的魏格纳相关能量泛函。[8]
交换相关势[编辑]与局域密度近似相对应的交换相关势由下式给出:[1]

在有限体系中,局域密度近似交换相关势在无穷远处以指数形式衰减,这种渐近行为是错误的。真实的交换相关势以慢得多的与距离成反比的速度衰减。这种不正常的渐近行为会影响束缚态的轨道数,并且无法用来描述里德堡态。这导致在计算中高估HOMO能量,使得基于库普曼斯定理进行的电离能计算结果不正确。进一步地,局域密度近似在描述富电子体系如负离子的时候表现不佳,常常因为无法将额外的电子纳入到束缚态中而给出体系不能稳定存在的错误结论。[9][10]
网络摘录及问答
http://cms.mpi.univie.ac.at/vasp-forum/forum_viewtopic.php?4.1117
QQQQ:
Hi,
One vasp user (see Feb 01 2005 in bug report forum) has already reported this.
For non-magnetic bulk calculation with LDA+U, I used
LDAUTYPE =4
(ISPIN =1 default) and a particular value of U & J (from the online manual double counting correction for LDA+U containts J so J needs to be given even for non-magnetic runs, although not conceivable why for non-magnetic system one needs J).
But the run stops before the first electronic SCF starts.
In the Feb 01 2005 reply to the vasp user, admin suggested to use ISPIN =2 with LDAUTYPE =4.
But is n't ISPIN=2, LDAUTYPE =4 means one is doing SPIN-POLARIZED calculation for non-magnetic system?
Also the vasp user (Feb 01, 2005 query) said ISPIN=1 and LDAUTYPE= 2 worked for his non-magnetic calculation. If
Dudarev's apparoach (LDAUTYPE =2 ) is for spin-polarized system, then how ISPIN=1, LDAUTYPE=2 worked for him/her?
AAAAA:
Dear Sahu,
in general for the two DFT+U approaches implemented in VASP you have to
set ISPIN=2.
The Lichtenstein technique as well as the Dudarev approach are
formulated such that the electron spin, i.e. the z-component, is explicitely included. Hence, you have to perform spin-polarized calculations and all DFT+U calculations with ISPIN=1 are useless. When you describe a system with DFT+U you introduce by definition magnetic moments and impose a particular ordering of the moments although a system might be non-magnetic. For example, most of the physical and structural properties of delta-Pu are well described by DFT+U. However, delta-Pu is non-magnetic
and DFT+U imposes magnetism artificially.
The only difference between the DFT+U methods defined by LDAUTYPE=1 and LDAUTYPE=2 is which double counting correction is used. Thats all.
Sahu
https://blog.sciencenet.cn/blog-567091-759805.html
上一篇:电子结构学习:Heavy ferimion and related superconductor
下一篇:表面反应、单晶制备与光发射电子显微镜