代数学方向期刊分层指南(DeepSeek版)，欢迎提建议。

期刊的“排行榜”并非一个绝对、官方的概念，尤其在数学领域，其评价体系更注重学术声誉、文章质量和历史传承，而非简单的引用指标。不过，根据长期的学术共识、发表难度、编委水准和影响力，我们可以对代数学领域的期刊进行一个分层和分类，这比一个单一的“榜单”更有参考价值。 以下为您梳理的代数学方向期刊分层指南，综合了领域内的普遍认知： 第一梯队：数学综合顶刊 这些是数学界公认的“皇冠明珠”，发表所有数学分支最具突破性的成果。在代数领域做出根本性贡献的工作会发表于此。 Annals of Mathematics - 公认的数学界最高荣誉期刊之一。 Inventiones Mathematicae - 与《Annals》齐名的顶级综合性期刊。 Journal of the American Mathematical Society - 美国数学学会旗舰刊，发表最重大、影响深远的成果。 Publications Mathématiques de l‘IHÉS - 法国高等科学研究所出版，以发表长篇、奠基性论文著称。 第二梯队：代数学专门顶刊 这是代数学家最核心的“目标期刊”。它们专注于代数及其子领域，发表该方向最重大、最完整的成果。 Journal für die reine und angewandte Mathematik (Crelles Journal) - 世界上最古老的数学期刊之一，在代数等领域享有极高声誉。 Compositio Mathematica - 发表高质量、完整的综合性研究论文。 Advances in Mathematics - 涵盖纯数与应用数学，代数方面非常强势。 American Journal of Mathematics - 美国最古老的数学期刊之一，在代数几何、数论、表示论等领域传统深厚。 Mathematische Annalen - 另一本历史悠久的德国综合性顶刊，代数文章质量极高。 第三梯队：核心分支领域顶级/重要期刊 这个层级的期刊在各自的具体分支领域内被视为顶级或非常重要。发表难度依然很高，是领域内主流成果的主要出口。 代数几何与数论（算术几何）： Algebra & Number Theory Mathematical Research Letters (文章较短，但标准极高) International Mathematics Research Notices (IMRN) 表示论、李理论与代数群： Representation Theory Transformation Groups Journal of Algebra (见下，是代数领域的核心综合性期刊) 同调代数、范畴论、交换代数： Journal of Algebra (特别注意)：这是代数学领域覆盖面最广、最具代表性的核心期刊。虽然影响因子不是最高，但发表文章体量巨大，覆盖代数所有子方向，是衡量一个代数学家产出的重要标杆。它的声誉稳固，可视为第二与第三梯队之间的重要桥梁。 Selecta Mathematica (New Series) Transactions of the American Mathematical Society (综合性，但代数文章很多) 代数组合与相关领域： Journal of Combinatorial Theory, Series A Advances in Applied Mathematics 第四梯队：其他重要期刊与快速发表期刊 这些是发表扎实、优秀工作的好期刊，在特定社区内很受尊重。同时也包括一些以审稿快、文章短为特点的期刊。 Proceedings of the American Mathematical Society Journal of Pure and Applied Algebra Communications in Algebra (发表大量代数各领域的研究) Algebraic Geometry (开放获取，影响力上升很快) Proceedings of the London Mathematical Society (英国数学界的代表性期刊) Bulletin of the London Mathematical Society (发表综述和重要短论文) Bulletin des Sciences Mathématiques (法国传统强刊) Journal of the London Mathematical Society (Second Series)

专业建议与说明 数学期刊评价的特殊性：数学界，尤其是纯数学，极度不依赖影响因子（IF）。期刊的声誉建立在数十年甚至上百年的学术积淀之上，由编委和审稿人的权威性、过往发表文章的经典程度共同决定。 优先考虑子领域契合度：对于具体工作，首先应考虑期刊的范围（Scope）。一篇优秀的表示论文章，发表在 Representation Theory 或 Journal of Algebra 可能比发表在综合性顶刊更对读者胃口。 关注论文预印本平台：现代数学交流高度依赖 arXiv。论文的“发表”过程通常是：先上传arXiv确立优先级，然后投稿至期刊。文章的影响力在投稿前就可能已在社区内传播开。 参考同行与导师的意见：最直接的参考是您所在细分领域的资深学者（合作者、导师、同行）通常将哪些期刊视为“好期刊”和“目标期刊”。 发表策略： 追求卓越：若认为自己做出了具有广泛影响力的突破性工作，应首先尝试第一、第二梯队的期刊。 领域深耕：高质量、完整的专业性工作，瞄准第三梯队的专门期刊是绝佳选择。 快速传播：对于精巧、完整但体量不大的结果，可以考虑 IMRN、Proceedings of the AMS 等。

为了更直观地呈现，以下是上述期刊分类的概要总结： 梯队 类别 主要特点与示例期刊 第一梯队 数学综合顶刊 所有数学分支的“皇冠期刊”，发表最重大突破。 例如：Ann. Math., Invent. Math., J. Amer. Math. Soc., Publ. Math. IHÉS 第二梯队 代数学专门顶刊 代数领域的核心目标期刊，发表该方向最完整、重要的成果。 例如：J. Reine Angew. Math., Compos. Math., Adv. Math., Amer. J. Math. 第三梯队 核心分支领域顶级期刊 在各代数子领域内被视为顶级或主流，是大部分重要成果的发表地。 例如：Algebra Number Theory, J. Algebra, Represent. Theory, Trans. Amer. Math. Soc. 第四梯队 其他重要及快速发表期刊 发表扎实工作、受社区尊重，或审稿较快的期刊。 例如：Proc. Amer. Math. Soc., J. Pure Appl. Algebra, Commun. Algebra, Bull. Lond. Math. Soc. 希望这份基于学术共识的分层指南对您的研究和投稿规划有所帮助！代数学的进展离不开高质量期刊的承载与传播，祝您科研顺利，成果丰硕！为了更直观地呈现，以下是上述期刊分类的概要总结：

梯队 类别 主要特点与示例期刊 第一梯队 数学综合顶刊 所有数学分支的“皇冠期刊”，发表最重大突破。 例如：Ann. Math., Invent. Math., J. Amer. Math. Soc., Publ. Math. IHÉS 第二梯队 代数学专门顶刊 代数领域的核心目标期刊，发表该方向最完整、重要的成果。 例如：J. Reine Angew. Math., Compos. Math., Adv. Math., Amer. J. Math. 第三梯队 核心分支领域顶级期刊 在各代数子领域内被视为顶级或主流，是大部分重要成果的发表地。 例如：Algebra Number Theory, J. Algebra, Represent. Theory, Trans. Amer. Math. Soc. 第四梯队 其他重要及快速发表期刊 发表扎实工作、受社区尊重，或审稿较快的期刊。 例如：Proc. Amer. Math. Soc., J. Pure Appl. Algebra, Commun. Algebra, Bull. Lond. Math. Soc.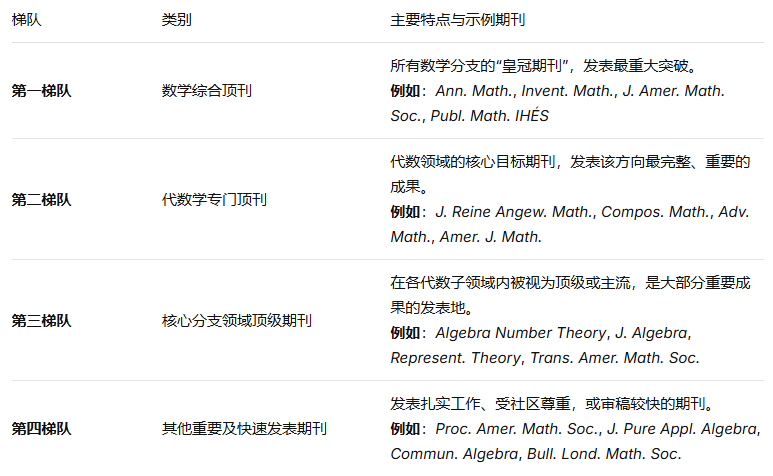

希望这份基于学术共识的分层指南对大家的研究和投稿规划有所帮助！代数学的进展离不开高质量期刊的承载与传播。

期刊的“排行榜”并非一个绝对、官方的概念，尤其在数学领域，其评价体系更注重学术声誉、文章质量和历史传承，而非简单的引用指标。不过，根据长期的学术共识、发表难度、编委水准和影响力，我们可以对代数学领域的期刊进行一个分层和分类，这比一个单一的“榜单”更有参考价值。 以下为您梳理的代数学方向期刊分层指南，综合了领域内的普遍认知： 第一梯队：数学综合顶刊 这些是数学界公认的“皇冠明珠”，发表所有数学分支最具突破性的成果。在代数领域做出根本性贡献的工作会发表于此。 Annals of Mathematics - 公认的数学界最高荣誉期刊之一。 Inventiones Mathematicae - 与《Annals》齐名的顶级综合性期刊。 Journal of the American Mathematical Society - 美国数学学会旗舰刊，发表最重大、影响深远的成果。 Publications Mathématiques de l‘IHÉS - 法国高等科学研究所出版，以发表长篇、奠基性论文著称。 第二梯队：代数学专门顶刊 这是代数学家最核心的“目标期刊”。它们专注于代数及其子领域，发表该方向最重大、最完整的成果。 Journal für die reine und angewandte Mathematik (Crelles Journal) - 世界上最古老的数学期刊之一，在代数等领域享有极高声誉。 Compositio Mathematica - 发表高质量、完整的综合性研究论文。 Advances in Mathematics - 涵盖纯数与应用数学，代数方面非常强势。 American Journal of Mathematics - 美国最古老的数学期刊之一，在代数几何、数论、表示论等领域传统深厚。 Mathematische Annalen - 另一本历史悠久的德国综合性顶刊，代数文章质量极高。 第三梯队：核心分支领域顶级/重要期刊 这个层级的期刊在各自的具体分支领域内被视为顶级或非常重要。发表难度依然很高，是领域内主流成果的主要出口。 代数几何与数论（算术几何）： Algebra & Number Theory Mathematical Research Letters (文章较短，但标准极高) International Mathematics Research Notices (IMRN) 表示论、李理论与代数群： Representation Theory Transformation Groups Journal of Algebra (见下，是代数领域的核心综合性期刊) 同调代数、范畴论、交换代数： Journal of Algebra (特别注意)：这是代数学领域覆盖面最广、最具代表性的核心期刊。虽然影响因子不是最高，但发表文章体量巨大，覆盖代数所有子方向，是衡量一个代数学家产出的重要标杆。它的声誉稳固，可视为第二与第三梯队之间的重要桥梁。 Selecta Mathematica (New Series) Transactions of the American Mathematical Society (综合性，但代数文章很多) 代数组合与相关领域： Journal of Combinatorial Theory, Series A Advances in Applied Mathematics 第四梯队：其他重要期刊与快速发表期刊 这些是发表扎实、优秀工作的好期刊，在特定社区内很受尊重。同时也包括一些以审稿快、文章短为特点的期刊。 Proceedings of the American Mathematical Society Journal of Pure and Applied Algebra Communications in Algebra (发表大量代数各领域的研究) Algebraic Geometry (开放获取，影响力上升很快) Proceedings of the London Mathematical Society (英国数学界的代表性期刊) Bulletin of the London Mathematical Society (发表综述和重要短论文) Bulletin des Sciences Mathématiques (法国传统强刊) Journal of the London Mathematical Society (Second Series) 给您的专业建议与说明 数学期刊评价的特殊性：数学界，尤其是纯数学，极度不依赖影响因子（IF）。期刊的声誉建立在数十年甚至上百年的学术积淀之上，由编委和审稿人的权威性、过往发表文章的经典程度共同决定。 优先考虑子领域契合度：对于具体工作，首先应考虑期刊的范围（Scope）。一篇优秀的表示论文章，发表在 Representation Theory 或 Journal of Algebra 可能比发表在综合性顶刊更对读者胃口。 关注论文预印本平台：现代数学交流高度依赖 arXiv。论文的“发表”过程通常是：先上传arXiv确立优先级，然后投稿至期刊。文章的影响力在投稿前就可能已在社区内传播开。 参考同行与导师的意见：最直接的参考是您所在细分领域的资深学者（合作者、导师、同行）通常将哪些期刊视为“好期刊”和“目标期刊”。 发表策略： 追求卓越：若认为自己做出了具有广泛影响力的突破性工作，应首先尝试第一、第二梯队的期刊。 领域深耕：高质量、完整的专业性工作，瞄准第三梯队的专门期刊是绝佳选择。 快速传播：对于精巧、完整但体量不大的结果，可以考虑 IMRN、Proceedings of the AMS 等。 为了更直观地呈现，以下是上述期刊分类的概要总结： 梯队 类别 主要特点与示例期刊 第一梯队 数学综合顶刊 所有数学分支的“皇冠期刊”，发表最重大突破。 例如：Ann. Math., Invent. Math., J. Amer. Math. Soc., Publ. Math. IHÉS 第二梯队 代数学专门顶刊 代数领域的核心目标期刊，发表该方向最完整、重要的成果。 例如：J. Reine Angew. Math., Compos. Math., Adv. Math., Amer. J. Math. 第三梯队 核心分支领域顶级期刊 在各代数子领域内被视为顶级或主流，是大部分重要成果的发表地。 例如：Algebra Number Theory, J. Algebra, Represent. Theory, Trans. Amer. Math. Soc. 第四梯队 其他重要及快速发表期刊 发表扎实工作、受社区尊重，或审稿较快的期刊。 例如：Proc. Amer. Math. Soc., J. Pure Appl. Algebra, Commun. Algebra, Bull. Lond. Math. Soc. 希望这份基于学术共识的分层指南对您的研究和投稿规划有所帮助！代数学的进展离不开高质量期刊的承载与传播，祝您科研顺利，成果丰硕！期刊的“排行榜”并非一个绝对、官方的概念，尤其在数学领域，其评价体系更注重学术声誉、文章质量和历史传承，而非简单的引用指标。不过，根据长期的学术共识、发表难度、编委水准和影响力，我们可以对代数学领域的期刊进行一个分层和分类，这比一个单一的“榜单”更有参考价值。 以下为您梳理的代数学方向期刊分层指南，综合了领域内的普遍认知： 第一梯队：数学综合顶刊 这些是数学界公认的“皇冠明珠”，发表所有数学分支最具突破性的成果。在代数领域做出根本性贡献的工作会发表于此。 Annals of Mathematics - 公认的数学界最高荣誉期刊之一。 Inventiones Mathematicae - 与《Annals》齐名的顶级综合性期刊。 Journal of the American Mathematical Society - 美国数学学会旗舰刊，发表最重大、影响深远的成果。 Publications Mathématiques de l‘IHÉS - 法国高等科学研究所出版，以发表长篇、奠基性论文著称。 第二梯队：代数学专门顶刊 这是代数学家最核心的“目标期刊”。它们专注于代数及其子领域，发表该方向最重大、最完整的成果。 Journal für die reine und angewandte Mathematik (Crelles Journal) - 世界上最古老的数学期刊之一，在代数等领域享有极高声誉。 Compositio Mathematica - 发表高质量、完整的综合性研究论文。 Advances in Mathematics - 涵盖纯数与应用数学，代数方面非常强势。 American Journal of Mathematics - 美国最古老的数学期刊之一，在代数几何、数论、表示论等领域传统深厚。 Mathematische Annalen - 另一本历史悠久的德国综合性顶刊，代数文章质量极高。 第三梯队：核心分支领域顶级/重要期刊 这个层级的期刊在各自的具体分支领域内被视为顶级或非常重要。发表难度依然很高，是领域内主流成果的主要出口。 代数几何与数论（算术几何）： Algebra & Number Theory Mathematical Research Letters (文章较短，但标准极高) International Mathematics Research Notices (IMRN) 表示论、李理论与代数群： Representation Theory Transformation Groups Journal of Algebra (见下，是代数领域的核心综合性期刊) 同调代数、范畴论、交换代数： Journal of Algebra (特别注意)：这是代数学领域覆盖面最广、最具代表性的核心期刊。虽然影响因子不是最高，但发表文章体量巨大，覆盖代数所有子方向，是衡量一个代数学家产出的重要标杆。它的声誉稳固，可视为第二与第三梯队之间的重要桥梁。 Selecta Mathematica (New Series) Transactions of the American Mathematical Society (综合性，但代数文章很多) 代数组合与相关领域： Journal of Combinatorial Theory, Series A Advances in Applied Mathematics 第四梯队：其他重要期刊与快速发表期刊 这些是发表扎实、优秀工作的好期刊，在特定社区内很受尊重。同时也包括一些以审稿快、文章短为特点的期刊。 Proceedings of the American Mathematical Society Journal of Pure and Applied Algebra Communications in Algebra (发表大量代数各领域的研究) Algebraic Geometry (开放获取，影响力上升很快) Proceedings of the London Mathematical Society (英国数学界的代表性期刊) Bulletin of the London Mathematical Society (发表综述和重要短论文) Bulletin des Sciences Mathématiques (法国传统强刊) Journal of the London Mathematical Society (Second Series) 给您的专业建议与说明 数学期刊评价的特殊性：数学界，尤其是纯数学，极度不依赖影响因子（IF）。期刊的声誉建立在数十年甚至上百年的学术积淀之上，由编委和审稿人的权威性、过往发表文章的经典程度共同决定。 优先考虑子领域契合度：对于具体工作，首先应考虑期刊的范围（Scope）。一篇优秀的表示论文章，发表在 Representation Theory 或 Journal of Algebra 可能比发表在综合性顶刊更对读者胃口。 关注论文预印本平台：现代数学交流高度依赖 arXiv。论文的“发表”过程通常是：先上传arXiv确立优先级，然后投稿至期刊。文章的影响力在投稿前就可能已在社区内传播开。 参考同行与导师的意见：最直接的参考是您所在细分领域的资深学者（合作者、导师、同行）通常将哪些期刊视为“好期刊”和“目标期刊”。 发表策略： 追求卓越：若认为自己做出了具有广泛影响力的突破性工作，应首先尝试第一、第二梯队的期刊。 领域深耕：高质量、完整的专业性工作，瞄准第三梯队的专门期刊是绝佳选择。 快速传播：对于精巧、完整但体量不大的结果，可以考虑 IMRN、Proceedings of the AMS 等。 为了更直观地呈现，以下是上述期刊分类的概要总结： 梯队 类别 主要特点与示例期刊 第一梯队 数学综合顶刊 所有数学分支的“皇冠期刊”，发表最重大突破。 例如：Ann. Math., Invent. Math., J. Amer. Math. Soc., Publ. Math. IHÉS 第二梯队 代数学专门顶刊 代数领域的核心目标期刊，发表该方向最完整、重要的成果。 例如：J. Reine Angew. Math., Compos. Math., Adv. Math., Amer. J. Math. 第三梯队 核心分支领域顶级期刊 在各代数子领域内被视为顶级或主流，是大部分重要成果的发表地。 例如：Algebra Number Theory, J. Algebra, Represent. Theory, Trans. Amer. Math. Soc. 第四梯队 其他重要及快速发表期刊 发表扎实工作、受社区尊重，或审稿较快的期刊。 例如：Proc. Amer. Math. Soc., J. Pure Appl. Algebra, Commun. Algebra, Bull. Lond. Math. Soc. 希望这份基于学术共识的分层指南对您的研究和投稿规划有所帮助！代数学的进展离不开高质量期刊的承载与传播，祝您科研顺利，成果丰硕！期刊的“排行榜”并非一个绝对、官方的概念，尤其在数学领域，其评价体系更注重学术声誉、文章质量和历史传承，而非简单的引用指标。不过，根据长期的学术共识、发表难度、编委水准和影响力，我们可以对代数学领域的期刊进行一个分层和分类，这比一个单一的“榜单”更有参考价值。 以下为您梳理的代数学方向期刊分层指南，综合了领域内的普遍认知： 第一梯队：数学综合顶刊 这些是数学界公认的“皇冠明珠”，发表所有数学分支最具突破性的成果。在代数领域做出根本性贡献的工作会发表于此。 Annals of Mathematics - 公认的数学界最高荣誉期刊之一。 Inventiones Mathematicae - 与《Annals》齐名的顶级综合性期刊。 Journal of the American Mathematical Society - 美国数学学会旗舰刊，发表最重大、影响深远的成果。 Publications Mathématiques de l‘IHÉS - 法国高等科学研究所出版，以发表长篇、奠基性论文著称。 第二梯队：代数学专门顶刊 这是代数学家最核心的“目标期刊”。它们专注于代数及其子领域，发表该方向最重大、最完整的成果。 Journal für die reine und angewandte Mathematik (Crelles Journal) - 世界上最古老的数学期刊之一，在代数等领域享有极高声誉。 Compositio Mathematica - 发表高质量、完整的综合性研究论文。 Advances in Mathematics - 涵盖纯数与应用数学，代数方面非常强势。 American Journal of Mathematics - 美国最古老的数学期刊之一，在代数几何、数论、表示论等领域传统深厚。 Mathematische Annalen - 另一本历史悠久的德国综合性顶刊，代数文章质量极高。 第三梯队：核心分支领域顶级/重要期刊 这个层级的期刊在各自的具体分支领域内被视为顶级或非常重要。发表难度依然很高，是领域内主流成果的主要出口。 代数几何与数论（算术几何）： Algebra & Number Theory Mathematical Research Letters (文章较短，但标准极高) International Mathematics Research Notices (IMRN) 表示论、李理论与代数群： Representation Theory Transformation Groups Journal of Algebra (见下，是代数领域的核心综合性期刊) 同调代数、范畴论、交换代数： Journal of Algebra (特别注意)：这是代数学领域覆盖面最广、最具代表性的核心期刊。虽然影响因子不是最高，但发表文章体量巨大，覆盖代数所有子方向，是衡量一个代数学家产出的重要标杆。它的声誉稳固，可视为第二与第三梯队之间的重要桥梁。 Selecta Mathematica (New Series) Transactions of the American Mathematical Society (综合性，但代数文章很多) 代数组合与相关领域： Journal of Combinatorial Theory, Series A Advances in Applied Mathematics 第四梯队：其他重要期刊与快速发表期刊 这些是发表扎实、优秀工作的好期刊，在特定社区内很受尊重。同时也包括一些以审稿快、文章短为特点的期刊。 Proceedings of the American Mathematical Society Journal of Pure and Applied Algebra Communications in Algebra (发表大量代数各领域的研究) Algebraic Geometry (开放获取，影响力上升很快) Proceedings of the London Mathematical Society (英国数学界的代表性期刊) Bulletin of the London Mathematical Society (发表综述和重要短论文) Bulletin des Sciences Mathématiques (法国传统强刊) Journal of the London Mathematical Society (Second Series) 给您的专业建议与说明 数学期刊评价的特殊性：数学界，尤其是纯数学，极度不依赖影响因子（IF）。期刊的声誉建立在数十年甚至上百年的学术积淀之上，由编委和审稿人的权威性、过往发表文章的经典程度共同决定。 优先考虑子领域契合度：对于具体工作，首先应考虑期刊的范围（Scope）。一篇优秀的表示论文章，发表在 Representation Theory 或 Journal of Algebra 可能比发表在综合性顶刊更对读者胃口。 关注论文预印本平台：现代数学交流高度依赖 arXiv。论文的“发表”过程通常是：先上传arXiv确立优先级，然后投稿至期刊。文章的影响力在投稿前就可能已在社区内传播开。 参考同行与导师的意见：最直接的参考是您所在细分领域的资深学者（合作者、导师、同行）通常将哪些期刊视为“好期刊”和“目标期刊”。 发表策略： 追求卓越：若认为自己做出了具有广泛影响力的突破性工作，应首先尝试第一、第二梯队的期刊。 领域深耕：高质量、完整的专业性工作，瞄准第三梯队的专门期刊是绝佳选择。 快速传播：对于精巧、完整但体量不大的结果，可以考虑 IMRN、Proceedings of the AMS 等。 为了更直观地呈现，以下是上述期刊分类的概要总结： 梯队 类别 主要特点与示例期刊 第一梯队 数学综合顶刊 所有数学分支的“皇冠期刊”，发表最重大突破。 例如：Ann. Math., Invent. Math., J. Amer. Math. Soc., Publ. Math. IHÉS 第二梯队 代数学专门顶刊 代数领域的核心目标期刊，发表该方向最完整、重要的成果。 例如：J. Reine Angew. Math., Compos. Math., Adv. Math., Amer. J. Math. 第三梯队 核心分支领域顶级期刊 在各代数子领域内被视为顶级或主流，是大部分重要成果的发表地。 例如：Algebra Number Theory, J. Algebra, Represent. Theory, Trans. Amer. Math. Soc. 第四梯队 其他重要及快速发表期刊 发表扎实工作、受社区尊重，或审稿较快的期刊。 例如：Proc. Amer. Math. Soc., J. Pure Appl. Algebra, Commun. Algebra, Bull. Lond. Math. Soc. 希望这份基于学术共识的分层指南对您的研究和投稿规划有所帮助！代数学的进展离不开高质量期刊的承载与传播，祝您科研顺利，成果丰硕！