博文
形式理论:将形式逻辑系统应用于具体对象领域的逻辑基础
||
[敬请读者注意] 本人保留本文的全部著作权利。如果哪位读者使用本文所描述内容,请务必如实引用并明白注明本文出处。如果本人发现任何人擅自使用本文任何部分内容而不明白注明出处,恕本人在网上广泛公布侵权者姓名。敬请各位读者注意,谢谢!
形式理论:将形式逻辑系统应用于具体对象领域的逻辑基础
程京德
一个形式逻辑系统由其形式语言(由该逻辑系统的符号表中的符号构成的合乎文法的逻辑式的集合,用来表达逻辑命题)和逻辑归结关系(定义在该逻辑系统的语言上的、从语言的幂集到语言的二元关系,用来表达从前提得出有效结论)这两个部分构成。依据对逻辑归结关系的不同表达方式,一个形式逻辑系统可以被表达为不同的演绎系统,比如,希尔伯特式形式化公理系统(Hilbert Style Formal Logic Systems)、根岑式自然演绎系统(Gentzen’s Natural Deduction System)、根岑式矢列演算系统(Gentzen’s Sequent Calculus System) 、语义表系统(Semantic Tableau System) 、解消原理系统(Resolution System)等等。但是,无论一个形式逻辑系统怎么被表达,其逻辑定理集合是一定不变的。
一个形式逻辑系统提供了对于论证和推理之正确性和有效性进行判断的某种一般的形式化标准。这个形式化标准可以被用来判断,对于给定的前提(由该形式逻辑系统的形式语言表达的逻辑式集合)能够得出什么样的正确结论(由该形式逻辑系统的形式语言表达的逻辑式)。不同的形式逻辑系统当然就提供了不同的标准。当我们要应用形式逻辑系统来解决具体对象领域内的问题的时候,首要的事情就是要根据目的来选择一个适当的逻辑系统。
从逻辑学的角度来说,逻辑学不关心各个具体对象领域内命题的真假对错,只关心从什么样的前提能够得出什么样的结论。
一个关于某个具体对象领域的形式理论是建立在一个选定形式逻辑系统之上的演绎系统。当我们选定某个形式逻辑系统作为逻辑基础,并且确定了具体对象领域内被我们认定为真的经验公理之后,我们就在理论上确定了一个关于该具体对象领域的形式理论。
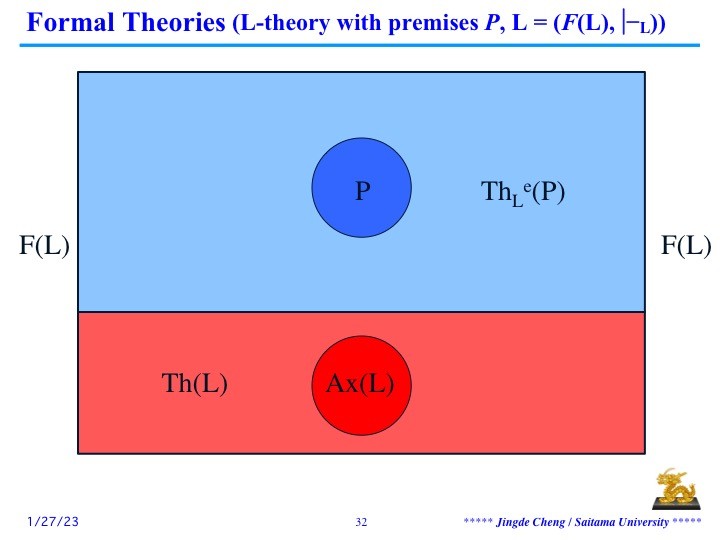
一个形式理论由两部分构成,其一为其基础逻辑系统的全部逻辑定理,其二为以经验公理为前提基于基础逻辑系统可以推出的所有经验定理。如下图所示:设所选定形式逻辑系统L的形式语言为F(L),F(L)中所有的逻辑式被以P为前提基于L的形式理论划分为三部分,逻辑理论部分(L的全部逻辑定理,图中用红色表示)、经验理论部分(以经验公理集合P为前提基于L可以推出的所有经验定理,图中用蓝色表示)、非理论部分(F(L)中所有不被该形式理论所承认的逻辑式,图中用白色表示)。
比如,NBG公理集合论或者ZF公理集合论,就都是基于经典数理逻辑一阶谓词演算的、具有等词(将相等定义为一个初始谓词)的形式理论。两者的逻辑理论部分都是具有等词的一阶谓词演算,经验公理集合分别为NBG公理或者ZF公理。
如果在一个形式逻辑系统内,从矛盾的前提可以推导出任意的逻辑式作为正确的结论, 则称该逻辑系统为爆炸的(explosive)。非爆炸的形式逻辑系统被称为準一致的(paraconsistent)。众所周知,经典数理逻辑是爆炸的。
如果一个形式理论的经验公理是矛盾的,则称该形式理论为直接(或明晰地)矛盾(或不一致)的(directly/explicitly inconsistent);如果一个形式理论不是直接矛盾的,但是其经验理论部分是矛盾的,则称该形式理论为间接(或隐含地)矛盾(或不一致)的(indirectly/implicitly inconsistent)。一个即非直接也非间接矛盾的形式理论被称为无矛盾(一致)的。
如果一个以L为基础逻辑系统的形式理论包含了L的形式语言F(L)中所有的逻辑式,则称其为爆炸的,非爆炸的形式理论被称为準一致的。
如果一个以爆炸的形式逻辑系统L为基础逻辑系统的形式理论是直接或间接矛盾的,那么该形式理论必定是爆炸的。显然,爆炸的形式理论毫无用处,因其根本无法用于区分具体对象领域中的真假对错。因为经典数理逻辑是爆炸的,所以它不能被应用到任何直接或间接矛盾的形式理论。
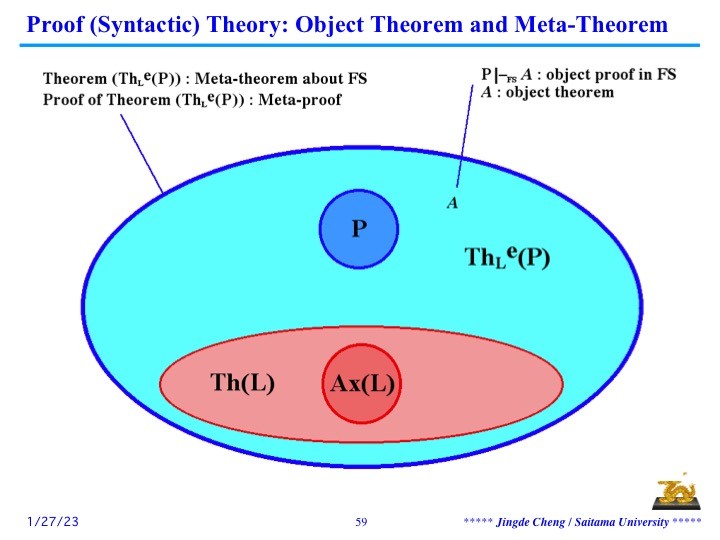
从理论的观点来看,对于一个形式理论,我们一般关心它有何整体上的性质,亦即,关于该形式理论自身的元定理,如下图所示。
比如,1931年,哥德尔证明了这样一个关于数论形式理论的元定理,对于一个足够丰富的数论形式理论,存在有不可被形式地证明的目标定理(构造出这样的目标定理的方法是可以给定的),即后来被称之为“哥德尔第一不完全定理”的著名定理。
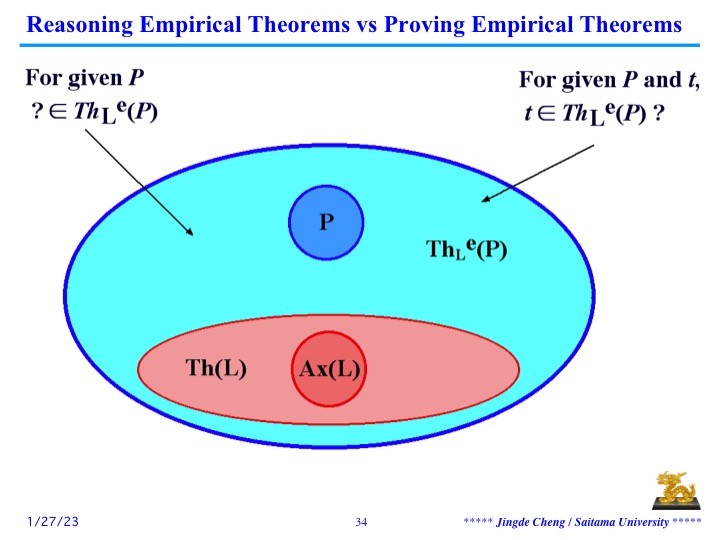
从应用的观点来看,对于一个形式理论,我们一般关心,我们能够发现什么经验定理,或者我们能够证明什么经验定理,如下图所示。
从应用自动化的观点来看,对于一个形式理论,我们一般关心,使用自动定理证明技术我们能够让计算机来自动证明什么经验定理,或者使用自动定理发现技术我们能够让计算机来自动发现什么经验定理。
微信公众号“数理逻辑与哲学逻辑”
https://blog.sciencenet.cn/blog-2371919-1375458.html
上一篇:以ChatGPT为代表的无偿式概率式自动生成工具之滥用将给人类社会带来什么后果?
下一篇:ChatGPT 的原理局限性:它永远不会做什么?