为了突出某个区域或局部数据的特性，便于数据的可视化和解释，常需要绘制二维区域填充图。MATLAB提供了三种类型的用于二维图形区域填充的绘图函数，具体是area函数、fill函数和patch函数。

area函数是Y数值对 x 坐标围成的面积图，该函数根据Y的形状填充曲线之间的区域。

fill函数是创建二维填充补片，即填充多边形区域绘制为补片，其顶点位于由X和Y指定的(x,y)位置，主要用于平面中多个区域的颜色填充。

patch函数是创建彩色多边形的补片，即将X和Y指定为每个顶点的坐标来创建一个或多个彩色多边形补片，主要用于平面中多边形的颜色填充。patch与fill函数功能和用法类似。

以下给出3个具体绘图示例。

clc; clear; close all;

% Demo 1

% ------------------------

% 加载数据

x = linspace(-8,12,100);

y1 = normpdf(x,4,6);  % Normal probability density function

y2 = normpdf(x,0,1).*0.5+normpdf(x,4,2).*0.5;

y3 = normpdf(x,-3,2);

y = [y1;y2;y3];

% 预设颜色

c = [184 194 140; 201 226 240; 250 181 157]./255; % Three colors

% 绘图

x = linspace(-8,12,100);

y1 = normpdf(x,4,6);% Normal probability density function

y2 = normpdf(x,0,1).*0.5+normpdf(x,4,2).*0.5;

y3 = normpdf(x,-3,2);

y = [y1;y2;y3];

fori = 1:size(y,1)

area(x,y(i,:),'FaceColor',c(i,:),'EdgeColor','none','FaceAlpha',0.5); hold on

end

% 坐标轴

xlabel('x/Samples'),ylabel('y/Value')

legend({'- Area No.1','- Area No.2','- Area No.3'})

set(gca,'XLim',[-8 12]);

% 修饰

defualtAxes

% ------------------------

程序运行结果如图B3-1所示。

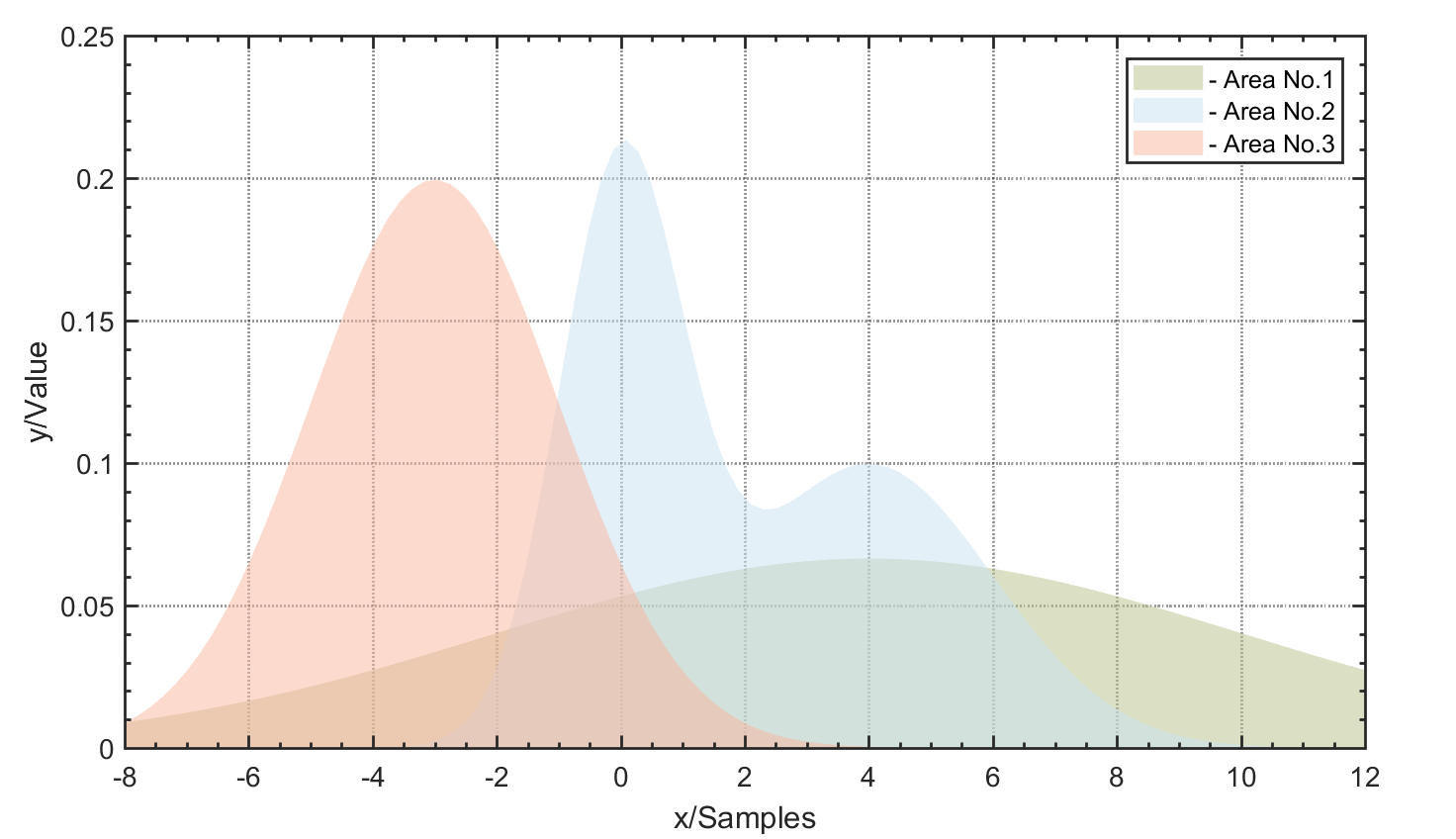
图B3-1 利用area函数据绘制面积填充图

如果填充过程要区分正负值，那么需要做出相应的零交叉点的判断，从而确定颜色的填充模式，这样就比较复杂。

一种简单的做法是，首先将数据拆分成正负两个序列，分别绘制填充图，这样实现起来就变得很简单了，不需要复杂的判断。

完整代码如下：

% Demo 2

%--------------------

load('plotData.mat');

y = data';

y = y(1,:)-10; % 产生正负值

x = linspace(0,10,length(y));

y1 = y; y1(y1<0)=0; % Negative value

y2 = y; y2(y2>0)=0; % Positive value

figure,

area(x,y1,'FaceColor','r','EdgeColor','r','FaceAlpha',0.6); hold on

area(x,y2,'FaceColor','b','EdgeColor','b','FaceAlpha',0.6);

xlabel('x-axis/Samples'),ylabel('y-axis/Intensity value')

set(gca,'FontName','Times New Roman','FontSize',12)

legend({'- Positive value area','- Negative value area'})

set(gcf,'Color','White');  % Background is white

% 修饰

defualtAxes

%--------------------

程序运行结果如图B3-2所示。

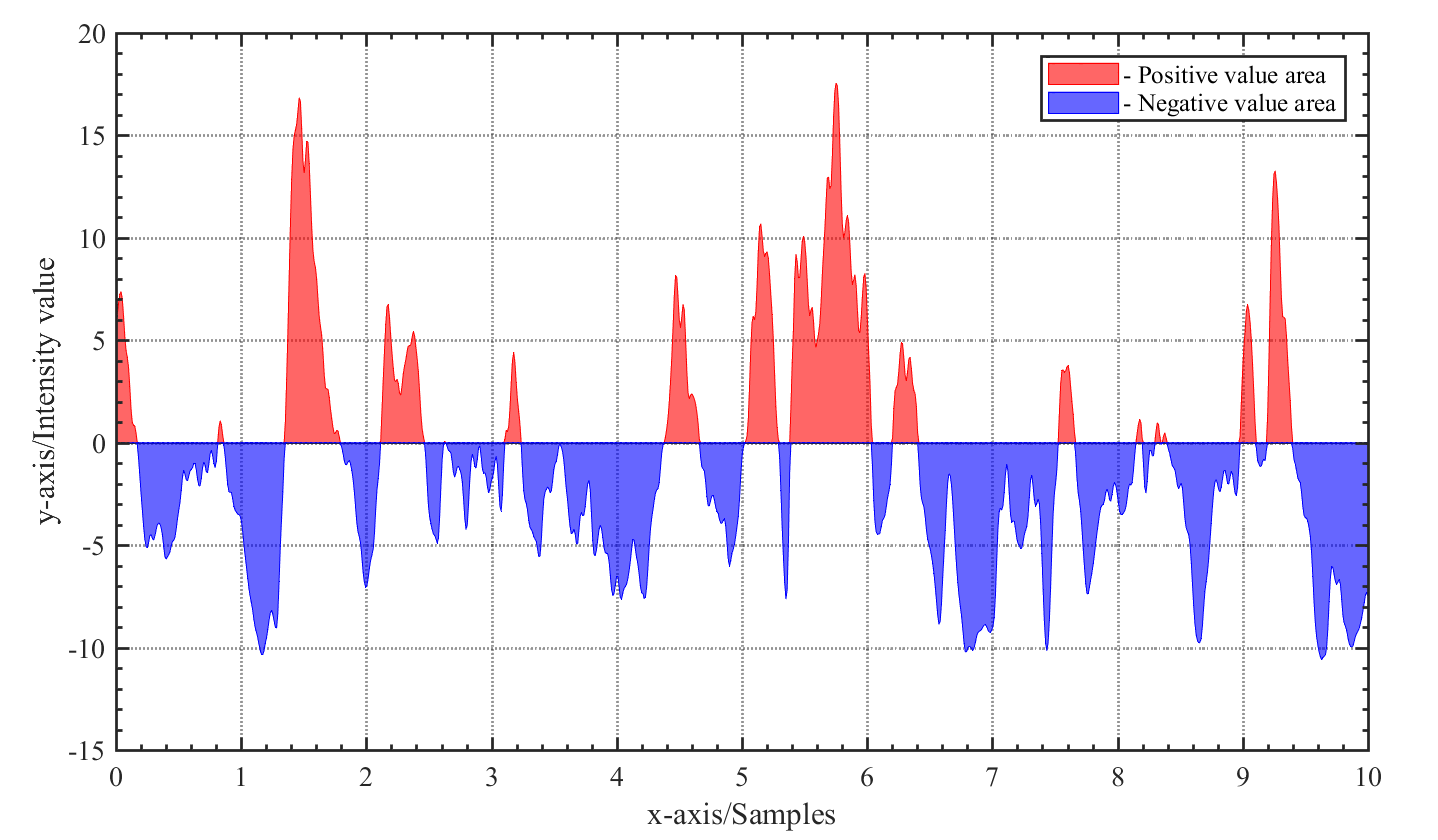
图B3-2 利用area函数绘制区分正负值的面积填充图

以上area函数主要针对与坐标轴围成的区域的填充，如果需要对图形窗口内任意闭合区域或多边形区域及进行填充，则需要用到fill和patch函数。

因为，这两个函数功能和用法类似，它们的基本用法MATLAB帮助文件均有详细说明。以下以fill函数为例，用一个稍复杂的应用为例进行说明。

首先，我们产生一条含随机噪声的Bessel分布数据。然后，对其进行多项式拟合，绘制拟合误差范围的置信度区间。

那么，只有一条曲线如何构成闭合区域？

我们可以按精度范围扩大y轴的数值范围，对应的x坐标从end端折回起始端，这样就形成了一个闭合曲线，也正包含了数据范围的闭环区域。

完整代码如下：

% Demo 3

%-------------------

x = 0 : 0.2 : 10;

y = besselj(0, x);% Bessel 函数

y = y+0.8*rand([1,length(x)]);

% 多项式拟合

[p,S] = polyfit(x,y,3);

[y_fit, delta] = polyval(p,x,S); % delta 标准误差估计值

%绘制原始数据、线性拟合及95%预测区间 y±2Δ

uy = y_fit+2*delta;

dy = y_fit-2*delta;

figure,

% 绘制原始数据

plot(x,y,'rx','LineWidth',1.5)

hold on

%绘制拟合曲线

plot(x,y_fit,'Color',[0 1 1],'LineWidth',1.5)

hold on

%绘制置信区间

xconf = [x x(end:-1:1)] ;% x坐标回转形成闭合区域

yconf = [uy dy(end:-1:1)]; % 扩大数据区间

c2 = [182,100,199]./255;

plot([x',x'],[uy',dy'],'Color',c2,'LineWidth',1.2,'LineStyle','--')

fill(xconf, yconf,'k','FaceColor',c2,'EdgeColor','none','FaceAlpha',0.1);

xlabel('x-axis/Samples'),ylabel('y-axis/Intensity value')

set(gca,'FontName','Times New Roman','FontSize',12)

legend({'- Data','- Linear fit','- 95% Prediction Interval'})

set(gcf,'Color','White');  % Background is white

% 修饰

defualtAxes

%--------------------

程序运行结果如图B3-3所示。

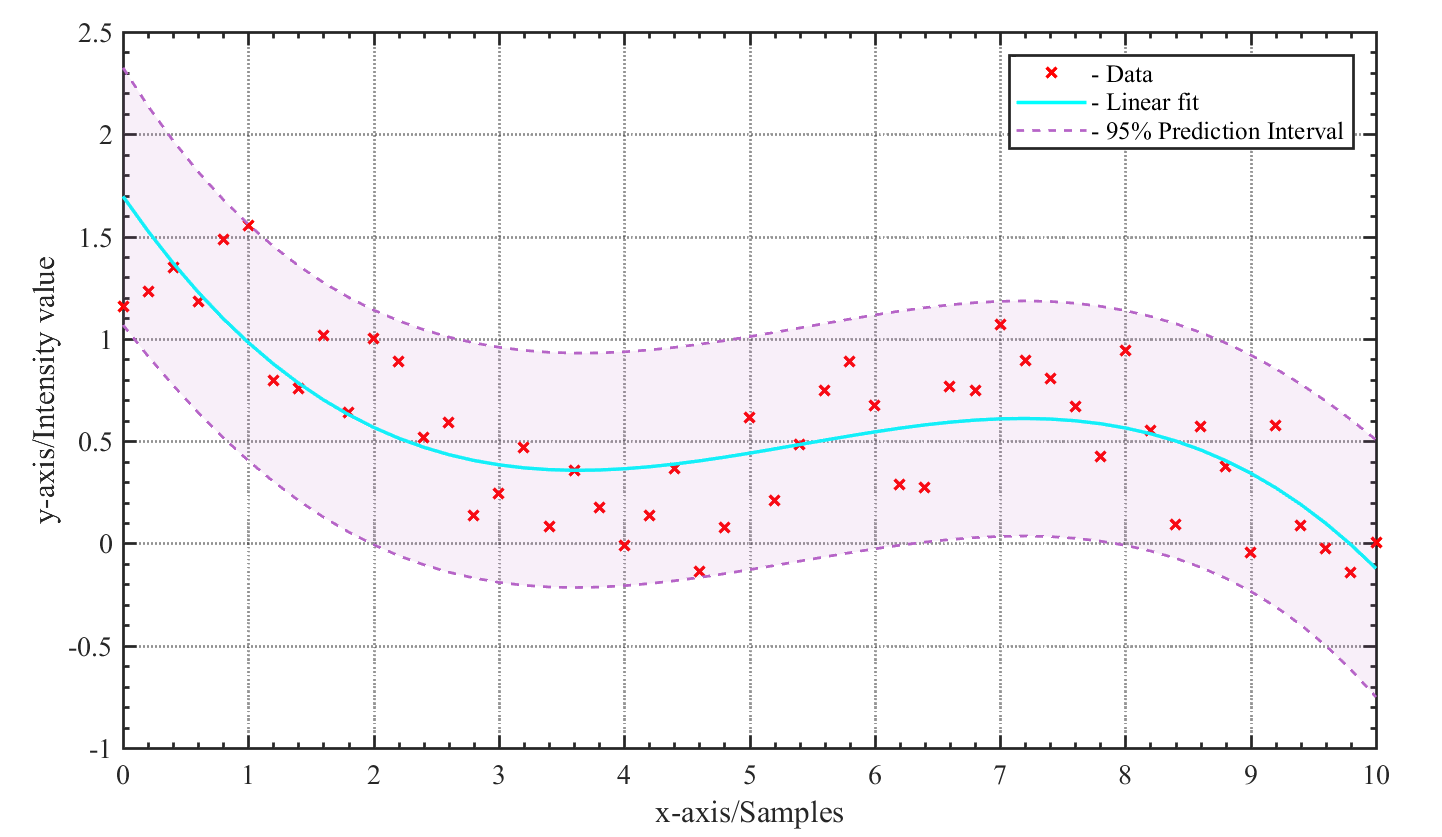
图B3-3 利用fill函数绘制数据置信区间图

以上用到的坐标轴修饰函数代码如下：

function defualtAxes

  ax=gca; hold on; box on

  ax.XGrid='on';

  ax.YGrid='on';

  ax.XMinorTick='on';

  ax.YMinorTick='on';

  ax.LineWidth=1.2;

  ax.GridLineStyle=':';

  %ax.FontName='Cambria';

  ax.FontSize=12;

  ax.GridAlpha=.5;

end

Demo3的实现代码中，用patch替换fill函数，也会得到基本一致的图形显示结果。

长按/扫一扫二维码，敬请关注“闻道研学”

参考来源：

[1] 微信公众号：slandarer随笔（ID: slandarer）

[2] 微信公众号：好玩的MATLAB（ID: EnjoyMatlab）

[3] Demo2数据：https://pan.baidu.com/s/1qAS1XT-4d3Xm3A1q0XZaug?pwd=74ze  提取码：74ze。

相关博文： 

[1] MATLAB绘图技巧-颜色渐变折线图

[2] MATLAB绘图技巧-折线图绘制

[2] MATLAB绘图技巧-颜色渐变柱状图绘制