研究背景及目的

张量分解已被广泛应用在图像处理、基因组信号处理、数据挖掘、计算机视觉、高阶统计等国际前沿领域。张量乘法的定义有好几类，例如，爱因斯坦积、t乘积、n-mode积、Tucker积等。张量的多维性和乘法的多样性使得研究张量分解远比研究矩阵分解复杂。

由于张量分解在数学及其他自然科学领域有着广泛的应用，不少数学家对其理论及应用进行了深入的研究。近二十年来，包括美国斯坦福大学、康奈尔大学、芝加哥大学、桑迪亚国家实验室、塔夫茨大学、犹他大学、法国格勒诺布尔大学、比利时鲁汶大学、瑞典林雪平大学、香港理工大学、香港浸会大学、北京大学等在内的世界著名大学的许多著名数学家对奇异值分解进行了深入的研究。

张量的t乘积是一种新型的张量积。2011年，美国塔夫茨大学M.E. Kilmer教授等首次建立了t乘积下单个3阶张量的奇异值分解定理，并将其用在图像处理中。2013年，美国詹姆斯麦迪逊大学C.D. Martin教授等将t乘积下单个p阶张量奇异值分解用于图像去噪和人脸识别中。自2011年以来，已有许多论文讨论了张量在t积下的分解及其应用。本文主要研究三个三阶张量在t积下的同时分解，即受限奇异值分解，及其在彩色图像处理上的应用，并提供了相应的数值示例。

研究过程及结果分析

本文首先建立了三个三阶张量在t乘积下的受限奇异值分解 (T-RSVD) 的理论。随后建立了张量T-RSVD的快速算法并给出了相关数值例子。作为推论，给出了T-PSVD和T-QSVD，它们是两个三阶张量在t乘积下的广义奇异值分解。本文理论推导的一个关键工具分块循环矩阵的正交对角化：

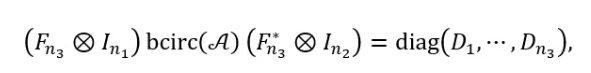
事实上，这得益于在应用t乘积时，张量所呈现出的结构，即循环矩阵。同时也正是因为t乘积的这种特性，促使作者将T-RSVD应用于图像处理中。这是因为，一张彩色图片𝐹可以与一个三阶张量𝒜一一对应，而bcirc(𝒜)的每一列 (或每一行)，即张量𝒜的三个不同正切面，则是𝐹对应于RGB三条通道中的数据。这表明，对两个三阶张量进行t积，则相当于对两张彩色图片进行变换。要特别指出的是，这种变换是对RGB三条通道同时进行的，所以对保存图片的信息特征有着重要意义。基于此，本文提出了一种基于T-RSVD的水印嵌入算法，能够在给定的彩色图像上同时嵌入三张彩色水印。作为对照，作者还将其与基于T-SVD的水印嵌入算法进行比较。由于T-SVD一次仅能分解一个张量，所以此情形下需要重复三次水印嵌入流程才能完成三张水印的添加。实验结果表明，与基于T-SVD的算法相比，基于T-RSVD的水印嵌入算法在不可感知性、鲁棒性和水印嵌入时间上表现更优。此外，无论水印添加的顺序或位置如何，采用本文所提算法处理的图像都能保持高度一致，而基于T-SVD的算法则会因水印添加的顺序或位置不同而产生显著差异。正如Mintzer和Braudaway曾提及的那样，当多个水印要满足不同的应用需求时，水印添加的顺序至关重要。而本文所提的水印同时嵌入算法正好回避了这一问题，表明了该算法的实用性和新颖性。

研究总结

本文主要工作是将复矩阵的受限奇异值分解推广至t积下的三阶张量上。作为应用，作者提供了一个将T-RSVD应用于彩色图像处理的数值示例，即水印嵌入算法。该算法的优势在于能够将多张彩色水印嵌入到给定的彩色图像中，从而提高信息隐藏能力和安全性。特别地，注意到四元数也是彩色图像处理的一个重要工具，以及近年来对广义四元数研究的兴起，例如，就在最近Chen、Wang和Xie给出了经典矩阵方程 𝐴𝑋𝐵=𝐶在对偶四元数上的可解性和通解的表达式。这些也为进一步研究基于广义四元数的图像处理提供了机会。同时为作者今后的工作提供了道路，即研究广义四元数张量在t积下的其它类似分解下及其应用，如在彩色视频中嵌入动态水印。希望本文的工作能对研究张量分解和多重水印嵌入算法的人员有所帮助。

阅读英文原文：https://www.mdpi.com/2727724

进入期刊英文主页：https://www.mdpi.com/journal/mathematics

作者介绍

张崇权 (Chong-Quan Zhang)

上海大学数学系，博士研究生；

新加坡国立大学与上海大学联合培养博士研究生；

研究方向：矩阵代数、四元数代数及其应用、数值代数。

王卿文 (Qing-Wen Wang)

上海大学二级教授、博士生导师、伟长学者；

中国高等教育学会教育数学专业委员会理事长、上海领军人才；

上海大学张量与矩阵理论国际研究中心主任；

研究方向：线性和多重线性代数、矩阵理论及应用、量子计算、数值代数、四元数统计。

王想想 (Xiang-Xiang Wang)

美国内华达大学里诺分校数学与统计系，博士研究生；

研究方向：矩阵代数、四元数统计、多元统计分析。

何卓衡 (Zhuo-Heng He)

上海大学数学系副教授、博士生导师；

中国高等教育学会教育数学专业委员会秘书长；

研究方向：矩阵代数、数值代数、四元数统计、信号处理。

Mathematics 期刊介绍

主编：Francisco Chiclana, School of Computer Science and Informatics, De Montfort University, UK

期刊主题涵盖纯数学和应用数学所有领域，重点发表代数、几何和拓扑、函数插值、差分和微分方程、计算和应用数学、概率与统计、数学物理、动力系统、工程数学、数学和计算机科学、数学生物学、网络科学、金融数学、以及模糊集、系统和决策等相关领域的文章。现已被SCIE (Web of Science)、Scopus等重要数据库收录，JCR Category Rank: 21/489 (Q1) 。

2023 Impact Factor：2.3

2023 CiteScore：4.0

Time to First Decision：17.1 Days

Acceptance to Publication：2.6 Days